Калейдоскоп из комбинаторных алгоритмов
Автоматическое построение лабиринтов
Тезей должен был найти выход из Критского лабиринта или погибнуть, убитый Минотавром. Но что поразительно: найти вход в лабиринт - задача не менее трудная.
Здесь не представляется возможным описать все мыслимые лабиринты, да это и
не требуется. Мы займемся простыми лабиринтами, построенными на
прямоугольнике  ,
где
,
где 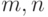 — положительные целые числа. Внутри и на границах
прямоугольника
поставлены стенки по ребрам покрывающей его единичной квадратной сетки. Чтобы
построить из прямоугольника лабиринт, выбьем одну единичную стенку на одной из
сторон прямоугольника (получится вход в лабиринт); выбьем одну единичную стенку
на противоположной стороне (получится выход) и еще удалим какое-то число строго
внутренних стенок. Говорят, что лабиринт имеет решение, если между входом и
выходом внутри лабиринта есть путь в виде ломаной, не имеющей общих точек со
стенками. Решение единственно, если любые два таких пути проходят через одни и
те же внутренние ячейки сетки. На рис. 17.1 приведен пример
лабиринта
— положительные целые числа. Внутри и на границах
прямоугольника
поставлены стенки по ребрам покрывающей его единичной квадратной сетки. Чтобы
построить из прямоугольника лабиринт, выбьем одну единичную стенку на одной из
сторон прямоугольника (получится вход в лабиринт); выбьем одну единичную стенку
на противоположной стороне (получится выход) и еще удалим какое-то число строго
внутренних стенок. Говорят, что лабиринт имеет решение, если между входом и
выходом внутри лабиринта есть путь в виде ломаной, не имеющей общих точек со
стенками. Решение единственно, если любые два таких пути проходят через одни и
те же внутренние ячейки сетки. На рис. 17.1 приведен пример
лабиринта  .
.
Один из возможных подходов к решению таков. Выбираем вход; затем, начав от него, добавляем по одной ячейке к главному пути-решению, пока он не достигнет выходной стороны. После этого удаляем некоторые внутренние стенки так, чтобы все клетки оказались соединенными с главным путем. Чтобы главный путь не получился прямым коридором, следует при его построении предусмотреть случайные повороты. Программа должна также следить за тем, чтобы при построении главного пути или при открытии боковых ячеек не нарушалась единственность решения. Наблюдательный читатель заметит, что определение единственности решения не годится в случае, когда путь заходит в боковой тупик и затем возвращается.
Программу можно написать почти на любом из процедурных языков.
Программа 1. Лабиринт.
{Программно задаются вход и выход. Нажимая на клавишу "Enter",
перебираем всевозможные пути от входа до выхода в лабиринте.
Выход из программы по клавише "Esc".
Алгоритм реализован на языке программирования Turbo-Pascal}
program Maze;
uses
Graph, Crt;
var
m,n: Integer;
Matrix: array [1..100,1..100] of Boolean;
Start,Finish: Integer;
procedure PrepareGraph;
var
Driver,Mode: Integer;
begin
Driver:=VGA;
Mode:=VGAHi;
InitGraph(Driver,Mode,'c:\borland\tp\bgi');
end;
procedure DisplayMaze(x1,y1,x2,y2: Integer);
var
i,j: Integer;
dx,dy: Real;
begin
SetFillStyle(1,8);
SetColor(15);
dx:=(x2-x1)/m;
dy:=(y2-y1)/n;
for i:=1 to n do
for j:=1 to m do
if not Matrix[i,j] then
Rectangle(Round(x1+(i-1)*dx),Round(y1+(j-1)*dy),
Round(x1+i*dx),Round(y1+j*dy));
end;
function CreatesPath(i,j: Integer): Boolean;
var
Result: Boolean;
Count: Integer;
ii,jj: Integer;
begin
Count:=0;
if (i>1) and Matrix[i-1,j] then Inc(Count);
if (i<m) and Matrix[i+1,j] then Inc(Count);
if (j>1) and Matrix[i,j-1] then Inc(Count);
if (j<m) and Matrix[i,j+1] then Inc(Count);
if Count>1 then Result:=true else Result:=false;
CreatesPath:=Result;
end;
function DeadEnd(i,j: Integer): Boolean;
var
Result: Boolean;
Count: Integer;
begin
Count:=0;
if (i=2) or CreatesPath(i-1,j) then Inc(Count);
if (i=m-1) or CreatesPath(i+1,j) then Inc(Count);
if (j=2) or CreatesPath(i,j-1) then Inc(Count);
if (j=n-1) or CreatesPath(i,j+1) then Inc(Count);
if Count=4 then Result:=true else Result:=false;
DeadEnd:=Result;
end;
function CreateMaze: Boolean;
var
i,j: Integer;
di,dj: Integer;
Result: Boolean;
begin
Randomize;
for i:=1 to n do
for j:=1 to m do Matrix[i,j]:=false;
Start:=Random(m-2)+2;
i:=Start;
j:=2;
Matrix[Start,1]:=true;
repeat
Matrix[i,j]:=true;
di:=0;
dj:=0;
while (di=0) and (dj=0) do begin
di:=1-Random(3);
if (i+di=1) or (i+di=m) then di:=0;
if di=0 then dj:=1-Random(3);
if j+dj=1 then dj:=0;
if CreatesPath(i+di,j+dj) then begin
di:=0;
dj:=0;
end;
end;
i:=i+di;
j:=j+dj;
until DeadEnd(i,j) or (j=n);
Finish:=i;
Matrix[Finish,n]:=true;
if j<n then Result:=false else Result:=true;
CreateMaze:=Result;
end;
begin
m:=6;
n:=6;
PrepareGraph;
repeat
ClearDevice;
repeat until CreateMaze;
DisplayMaze(120,40,520,440);
repeat until KeyPressed;
until ReadKey=#27;
CloseGraph;
end.Программа 2. Лабиринт.
{Лабиринт реализуется автоматически, без участия пользователя.
Алгоритм реализован на языке программирования Turbo-Pascal }
uses graph,crt;
var
mpos,npos,m,n,delx,x,y,t,gd,gm,i,k:integer;
begin
randomize;
writeln('Input labyrint size (x and y)');
readln(m,n);
writeln('Input entrance&exit coordinates (mpos<m and npos<m)');
readln(mpos,npos);
initgraph(gd,gm,'c:\borland\tp\bgi');
for i:=1 to m do
begin
for k:=1 to n do
begin
rectangle(90+10*i,90+10*k,90+10*i+10,90+10*k+10);
end;
end;
setfillstyle(1,0);
setcolor(0);
line(100+(mpos-1)*10+1,100,100+(mpos-1)*10+9,100);
line(100+(npos-1)*10+1,100+n*10,100+(npos-1)*10+9,100+n*10);
y:=n;
x:=npos;
readln;
while y>1 do
begin
delx:=random(m)-x+1;
if y=2 then delx:=mpos-x;
i:=91+x*10;
if i<90+(x+delx)*10 then
begin
while i<>90+(x+delx)*10 do
begin
i:=i+1;
line(i,91+y*10,i,99+y*10);
end;
end;
if i>91+(x+delx)*10 then
begin
while i<>91+(x+delx)*10 do
begin
i:=i-1;
line(i,91+y*10,i,99+y*10);
end;
end;
x:=x+delx;
line(91+10*x,90+y*10,99+10*x,90+y*10);
y:=y-1;
end;
readln;
end.
