Алгоритмы на графах
Поиск в глубину
При решении многих задач, касающихся ориентированных графов, необходим
эффективный метод систематического обхода вершин и дуг орграфов. Таким методом
является метод поиск в
глубину. Метод поиска в глубину является основой
многих эффективных алгоритмов работы с графами. Предположим, что есть
ориентированный граф  , в котором первоначально все вершины
помечены меткой "
, в котором первоначально все вершины
помечены меткой "  ". Поиск в глубину
начинается с выбора начальной вершины
". Поиск в глубину
начинается с выбора начальной вершины  орграфа
орграфа  ,
для этой вершины метка "
,
для этой вершины метка "  " меняется на метку
"
" меняется на метку
"  ". Затем для каждой вершины, смежной с
вершиной
". Затем для каждой вершины, смежной с
вершиной  и не посещаемой раньше, рекурсивно применяется поиск в
глубину. Когда все
вершины, которых можно достичь из вершины
и не посещаемой раньше, рекурсивно применяется поиск в
глубину. Когда все
вершины, которых можно достичь из вершины  , будут рассмотрены,
поиск заканчивается. Если некоторые вершины остались не
посещенными, то выбирается одна из них и алгоритм повторяется. Этот процесс
продолжается до тех пор, пока не будут обойдены все вершины орграфа
, будут рассмотрены,
поиск заканчивается. Если некоторые вершины остались не
посещенными, то выбирается одна из них и алгоритм повторяется. Этот процесс
продолжается до тех пор, пока не будут обойдены все вершины орграфа  .
.
Метод получил свое название - поиск в глубину, поскольку поиск не
посещенных вершин идет в направлении вглубь до тех пор, пока это возможно.
Например, пусть  является последней посещенной нами вершиной.
Выбираем очередную дугу
является последней посещенной нами вершиной.
Выбираем очередную дугу  (ребро), выходящую из вершины
(ребро), выходящую из вершины  . Возможна следующая альтернатива: вершина
. Возможна следующая альтернатива: вершина  помечена меткой "
помечена меткой "  "; вершина
"; вершина  помечена меткой "
помечена меткой "  ". Если вершина
". Если вершина  уже посещалась, то отыскивается другая вершина, смежная с
вершиной
уже посещалась, то отыскивается другая вершина, смежная с
вершиной  ; иначе вершина
; иначе вершина  метится меткой
"
метится меткой
"  " и поиск начинается заново от вершины
" и поиск начинается заново от вершины  . Пройдя все пути, которые начинаются в вершине
. Пройдя все пути, которые начинаются в вершине  ,
возвращаемся в вершину
,
возвращаемся в вершину  , то есть в ту вершину, из которой
впервые была достигнута вершина
, то есть в ту вершину, из которой
впервые была достигнута вершина  . Затем процесс повторяется, то
есть продолжается выбор нерассмотренных дуг,
исходящих из вершины
. Затем процесс повторяется, то
есть продолжается выбор нерассмотренных дуг,
исходящих из вершины  , и так до тех пор, пока не будут исчерпаны
все эти дуги.
, и так до тех пор, пока не будут исчерпаны
все эти дуги.
Алгоритм Дейкстры нахождения кратчайшего пути
Рассмотрим алгоритм нахождения путей в ориентированном графе. Пусть есть
ориентированный граф 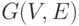 , у которого все дуги имеют
неотрицательные метки (веса дуг), а одна вершина
определена как источник.
Задача состоит в нахождении весов кратчайших
путей от источника ко всем другим вершинам граф
, у которого все дуги имеют
неотрицательные метки (веса дуг), а одна вершина
определена как источник.
Задача состоит в нахождении весов кратчайших
путей от источника ко всем другим вершинам граф 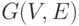 . Здесь
длина пути определяется как сумма весов дуг, составляющих путь. Эта задача
часто называется задачей нахождения кратчайшего пути с одним источником.
Отметим, что мы будем говорить о длине пути даже тогда, когда она измеряется в
других, не линейных, единицах измерения, например, во временных единицах или в
денежном эквиваленте.
. Здесь
длина пути определяется как сумма весов дуг, составляющих путь. Эта задача
часто называется задачей нахождения кратчайшего пути с одним источником.
Отметим, что мы будем говорить о длине пути даже тогда, когда она измеряется в
других, не линейных, единицах измерения, например, во временных единицах или в
денежном эквиваленте.
Можно представить орграф 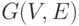 в виде карты маршрутов
рейсовых полетов из одного города в другой. Каждая вершина соответствует городу, а
ребро (дуга)
в виде карты маршрутов
рейсовых полетов из одного города в другой. Каждая вершина соответствует городу, а
ребро (дуга) 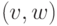 - рейсовому маршруту из города
- рейсовому маршруту из города  в город
в город  . Вес
дуги
. Вес
дуги 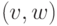 - это время полета из города
- это время полета из города  в город
в город  . В этом случае
решение задачи нахождения кратчайшего пути с одним источником для
ориентированного графа трактуется как минимальное время перелета между
различными городами.
. В этом случае
решение задачи нахождения кратчайшего пути с одним источником для
ориентированного графа трактуется как минимальное время перелета между
различными городами.
Для решения поставленной задачи будем использовать "жадный"
алгоритм, который называют алгоритмом Дейкстры (Dijkstra). Алгоритм строит множество  вершин, для которых кратчайшие пути от источника уже известны.
На каждом шаге к множеству
вершин, для которых кратчайшие пути от источника уже известны.
На каждом шаге к множеству  добавляется та из оставшихся вершин, расстояние до
которой от источника меньше,
чем для других оставшихся вершин. Если веса всех дуг неотрицательны, то можно
быть уверенным, что кратчайший путь от источника к конкретной вершине проходит
только через вершины множество
добавляется та из оставшихся вершин, расстояние до
которой от источника меньше,
чем для других оставшихся вершин. Если веса всех дуг неотрицательны, то можно
быть уверенным, что кратчайший путь от источника к конкретной вершине проходит
только через вершины множество  . Назовем такой путь особым. На каждом шаге
алгоритма используется также
массив
. Назовем такой путь особым. На каждом шаге
алгоритма используется также
массив  , в который записываются длины кратчайших особых путей
для каждой вершины.
Когда множество
, в который записываются длины кратчайших особых путей
для каждой вершины.
Когда множество  будет содержать все вершины орграфа, то есть
для всех вершин будут найдены особые
пути, тогда массив
будет содержать все вершины орграфа, то есть
для всех вершин будут найдены особые
пути, тогда массив  будет содержать длины кратчайших путей от
источника к каждой вершине.
будет содержать длины кратчайших путей от
источника к каждой вершине.
Алгоритм Флойда нахождения кратчайших путей между парами вершин
Предположим, что мы имеем помеченный орграф, который содержит время полета по маршрутам, связывающим определенные города, и~мы хотим построить таблицу, где приводилось бы минимальное время перелета из одного (произвольного) города в любой другой. В этом случае мы сталкиваемся с общей задачей нахождения кратчайших путей, то есть нахождения кратчайших путей между всеми парами вершин орграфа.
Формулировка задачи.Есть ориентированный граф 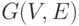 , каждой дуге
(ребру)
, каждой дуге
(ребру) 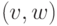 этого графа сопоставлен неотрицательный вес
этого графа сопоставлен неотрицательный вес  . Общая задача нахождения кратчайших путей заключается в нахождении для
каждой упорядоченной пары вершин
. Общая задача нахождения кратчайших путей заключается в нахождении для
каждой упорядоченной пары вершин 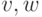 любого пути от вершины
любого пути от вершины  в вершину
в вершину  , длина которого минимальна среди всех возможных путей
от
, длина которого минимальна среди всех возможных путей
от  к
к  .
.
Можно решать эту задачу, последовательно применяя алгоритм Дейкстры для
каждой вершины, объявляемой в качестве источника. Но мы для решения
поставленной задачи воспользуемся алгоритмом, предложенным Флойдом (R.W.
Floyd). Пусть все вершины орграфа последовательно пронумерованы от 1 до  .
Алгоритм Флойда использует матрицу
.
Алгоритм Флойда использует матрицу  ,
в которой находятся длины кратчайших путей:
,
в которой находятся длины кратчайших путей:
 , если
, если 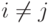 ;
;
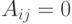 , если
, если  ;
;
 если отсутствует путь из вершины
если отсутствует путь из вершины  в вершину
в вершину  .
.
Над матрицей  выполняется
выполняется  итераций. После
итераций. После  -й итерации
-й итерации  содержит значение наименьшей
длины пути из вершины
содержит значение наименьшей
длины пути из вершины  в вершину
в вершину  , причем путь не
проходит через вершины с номерами большими
, причем путь не
проходит через вершины с номерами большими  .
.
Вычисление на  -ой итерации выполняется по формуле:
-ой итерации выполняется по формуле:  Верхний индекс
Верхний индекс  обозначает значение матрицы
обозначает значение матрицы  после
после  -ой итерации.
-ой итерации.
Для вычисления 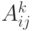 проводится сравнение величины
проводится сравнение величины  (то есть стоимость пути от вершины
(то есть стоимость пути от вершины  к вершине
к вершине  без участия
вершины
без участия
вершины  или другой вершины с более высоким номером) с величиной
или другой вершины с более высоким номером) с величиной  (стоимость пути от вершины
(стоимость пути от вершины  к вершине
к вершине  плюс стоимость пути от вершины
плюс стоимость пути от вершины  до вершины
до вершины  ). Если путь через
вершину
). Если путь через
вершину  дешевле, чем
дешевле, чем 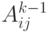 , то
величина
, то
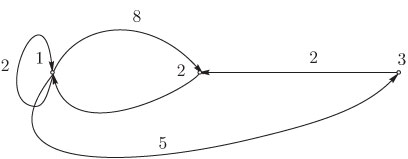
величина 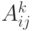 изменяется. Рассмотрим орграф:
изменяется. Рассмотрим орграф:
Матрица A(3 * 3) на нулевой итерации (k = 0)
![\left[ {\begin{array}{*{20}c}
0 & 8 & 5 \\
3 & 0 & \infty \\
\infty & 2 & 0 \\
\end{array} } \right]](/sites/default/files/tex_cache/ee1937107b420f4edeb8967c870c9713.png)
Матрица A(3 * 3) после первой итерации (k = 1)
![\left[ {\begin{array}{*{20}c}
0 & 8 & 5 \\
3 & 0 & 8 \\
\infty & 2 & 0 \\
\end{array} } \right]](/sites/default/files/tex_cache/494064cb493e7c39c30f705d701305ba.png)
Матрица A(3 * 3) после второй итерации (k = 2)
![\left[ {\begin{array}{*{20}c}
0 & 8 & 5 \\
3 & 0 & 8 \\
5 & 2 & 0 \\
\end{array} } \right]](/sites/default/files/tex_cache/176e77040e059dd0fef6ac7e58440892.png)
Матрица A(3 * 3) после третьей итерации (k = 3)
![\left[ {\begin{array}{*{20}c}
0 & 7 & 5 \\
3 & 0 & 8 \\
5 & 2 & 0 \\
\end{array} } \right]](/sites/default/files/tex_cache/c5f19f1373864febcbe37b0bbd1751c0.png)