Комбинаторика и ряды
Введение
Метод рекуррентных соотношений позволяет решать многие комбинаторные задачи. Но в целом ряде случаев рекуррентные соотношения довольно трудно составить, а еще труднее решить. Зачастую эти трудности удается обойти, использовав производящие функции. Поскольку понятие производящей функции связано с бесконечными степенными рядами, познакомимся с этими рядами.
Деление многочленов
Если заданы два многочлена  и
и  , то
всегда существуют многочлены
, то
всегда существуют многочлены 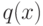 ( частное )
и
( частное )
и 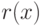 ( остаток ),
такие, что
( остаток ),
такие, что 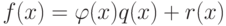 , причем степень
, причем степень 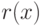 меньше степени
меньше степени  или
или 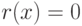 . При этом
. При этом  называется делимым,
а
называется делимым,
а  - делителем. Если же мы хотим, чтобы деление выполнялось без остатка,
то придется допустить в качестве частного не только многочлены, но и бесконечные
степенные ряды. Для получения
частного надо расположить многочлены по возрастающим степеням
- делителем. Если же мы хотим, чтобы деление выполнялось без остатка,
то придется допустить в качестве частного не только многочлены, но и бесконечные
степенные ряды. Для получения
частного надо расположить многочлены по возрастающим степеням  и
делить "углом", начиная с младших членов. Рассмотрим, например, деление
и
делить "углом", начиная с младших членов. Рассмотрим, например, деление  на
на 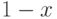
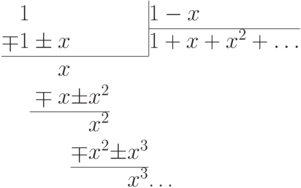
 в бесконечную десятичную дробь). С помощью индукции легко
убедиться, что все коэффициенты частного равны единице. Поэтому в качестве частного получается
бесконечный ряд
в бесконечную десятичную дробь). С помощью индукции легко
убедиться, что все коэффициенты частного равны единице. Поэтому в качестве частного получается
бесконечный ряд 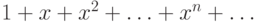 .
Вообще, если
.
Вообще, если  и
и  - два многочлена
- два многочлена
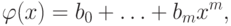
 многочлена
многочлена  отличен от нуля,
отличен от нуля,  , то при делении
, то при делении  на
на  получается бесконечный ряд
получается бесконечный ряд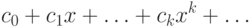 |
( 9.1) |
Лишь в случае, когда  делится без остатка на
делится без остатка на  , ряд (9.1) обрывается и мы получаем многочлен.
, ряд (9.1) обрывается и мы получаем многочлен.
Алгебраические дроби и степенные ряды
При делении многочлена  на многочлен
на многочлен 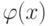 мы получаем бесконечный степенной ряд. Возникает вопрос: как связан
этот ряд с алгебраической дробью
мы получаем бесконечный степенной ряд. Возникает вопрос: как связан
этот ряд с алгебраической дробью 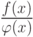 , то есть какой смысл можно придать записи
, то есть какой смысл можно придать записи
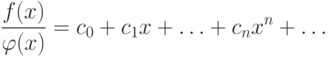 |
( 9.2) |
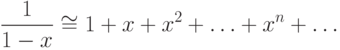 |
( 9.3) |
 .
Сначала положим
.
Сначала положим 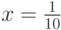 . Тогда левая часть соотношения примет значение
. Тогда левая часть соотношения примет значение  , а правая превратится в бесконечный числовой ряд
, а правая превратится в бесконечный числовой ряд 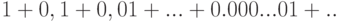 .
Так как мы не умеем складывать бесконечно много слагаемых, попробуем взять
сначала одно слагаемое, потом - два, потом - три и так далее слагаемых. Мы
получим такие суммы:
.
Так как мы не умеем складывать бесконечно много слагаемых, попробуем взять
сначала одно слагаемое, потом - два, потом - три и так далее слагаемых. Мы
получим такие суммы: 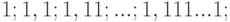
 . Ясно, что с возрастанием
. Ясно, что с возрастанием  эти суммы приближаются к значению
эти суммы приближаются к значению 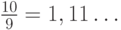 , которое приняла левая часть соотношения (9.3) при
, которое приняла левая часть соотношения (9.3) при 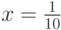 .
.То же самое получится, если вместо  подставить в обе части
(9.3) число
подставить в обе части
(9.3) число  . Левая часть равенства примет значение 2, а правая превратится в
бесконечный числовой ряд
. Левая часть равенства примет значение 2, а правая превратится в
бесконечный числовой ряд  Беря последовательно одно, два, три, четыре,
слагаемых, мы получим числа 1;
Беря последовательно одно, два, три, четыре,
слагаемых, мы получим числа 1;  ;
;  ;
; 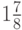 ,…,
,…,  . Ясно, что с возрастанием
. Ясно, что с возрастанием  эти числа стремятся к
числу 2.
эти числа стремятся к
числу 2.
Однако, если взять 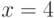 , то левая часть (9.3) примет значение
, то левая часть (9.3) примет значение 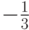 , а в правой получим ряд
, а в правой получим ряд  Если последовательно складывать члены этого ряда, то получаются суммы 1; 5;
21; 85; … Эти суммы неограниченно увеличиваются и не приближаются к числу
Если последовательно складывать члены этого ряда, то получаются суммы 1; 5;
21; 85; … Эти суммы неограниченно увеличиваются и не приближаются к числу 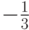 .
.
Мы встретились, таким образом, с двумя случаями. Чтобы их различать, введем общее понятие о сходимости и расходимости числового ряда. Пусть задан бесконечный числовой ряд
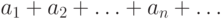 |
( 9.4) |
 , если разность
, если разность 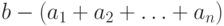 стремится к нулю при неограниченном увеличении
стремится к нулю при неограниченном увеличении  . Иными словами,
какое бы число
. Иными словами,
какое бы число 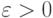 мы ни указали, отклонение
суммы
мы ни указали, отклонение
суммы 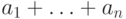 от
от  , начиная с
некоторого номера
, начиная с
некоторого номера 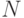 , окажется меньше
, окажется меньше  :
: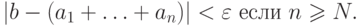
 называют суммой бесконечного ряда
называют суммой бесконечного ряда 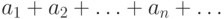 и пишут
и пишут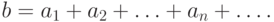
 , к которому сходится данный ряд (9.4),
то этот ряд называют расходящимся.
, к которому сходится данный ряд (9.4),
то этот ряд называют расходящимся.Проведенное выше исследование показывает, что
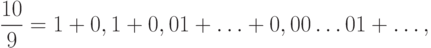
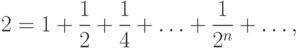
 ... расходится.
Более тщательное исследование показывает, что если
... расходится.
Более тщательное исследование показывает, что если  , то ряд
, то ряд 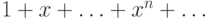 сходится к
сходится к 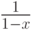 , а если
, а если  , то он
расходится. Чтобы доказать это утверждение, достаточно заметить, что
, то он
расходится. Чтобы доказать это утверждение, достаточно заметить, что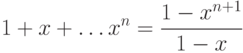
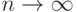 выражение
выражение  стремится
к нулю, если
стремится
к нулю, если 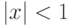 , и к бесконечности, если
, и к бесконечности, если  . При
. При 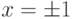 получаем расходящиеся числовые ряды
получаем расходящиеся числовые ряды  и
и  .Итак, если
.Итак, если 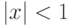 , то
, то |
( 9.5) |
Отметим, что равенство (9.5) - это известная из школьного курса математики формула для суммы бесконечно убывающей геометрической прогрессии.
Мы выяснили, таким образом, смысл записи
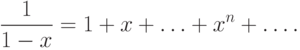
 , лежащих в некоторой области,
а именно при
, лежащих в некоторой области,
а именно при 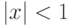 , стоящий справа ряд
сходится к
, стоящий справа ряд
сходится к 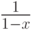 . Говорят, что функция
. Говорят, что функция 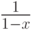 при
при 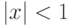 разлагается в
степенной ряд
разлагается в
степенной ряд 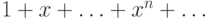 .Теперь уже можно выяснить и более общий вопрос.
.Теперь уже можно выяснить и более общий вопрос.Пусть при делении многочлена  на многочлен
на многочлен 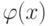 получился степенной ряд
получился степенной ряд
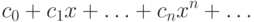 |
( 9.6) |
 ряд (9.6)
сходится к
ряд (9.6)
сходится к 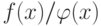 . Размеры области сходимости зависят от корней
знаменателя, то есть чисел, при которых знаменатель обращается в нуль.
Именно, если эти числа равны
. Размеры области сходимости зависят от корней
знаменателя, то есть чисел, при которых знаменатель обращается в нуль.
Именно, если эти числа равны 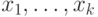 и
и 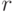 -
наименьшее из чисел
-
наименьшее из чисел 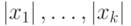 , то ряд
сходится в области
, то ряд
сходится в области  .
.Иными словами, всегда есть область  , в
которой выполняется равенство
, в
которой выполняется равенство
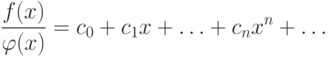 |
( 9.7) |
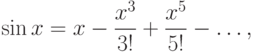
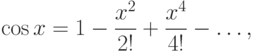

 не может иметь двух различных разложений в степенные ряды.
не может иметь двух различных разложений в степенные ряды.