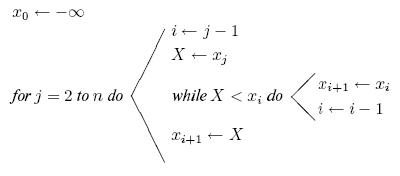Сортировка (часть 1)
Введение
Рассматриваемые здесь задачи можно отнести к наиболее часто встречающимся классам комбинаторных задач. Почти во всех машинных приложениях множество объектов должно быть переразмещено в соответствии с некоторым заранее определенным порядком. Например, при обработке коммерческих данных часто бывает необходимо расположить их по алфавиту или по возрастанию номеров. В числовых расчетах иногда требуется знать наибольший корень многочлена, и т.д.
Будем считать заданной таблицу с  именами, обозначаемыми
именами, обозначаемыми  ,
, 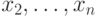 . Каждое имя
. Каждое имя  принимает
значение из пространства имен, на котором определен линейный порядок.
Будем считать, что никакие два имени не имеют одинаковых значений; то есть
любые
принимает
значение из пространства имен, на котором определен линейный порядок.
Будем считать, что никакие два имени не имеют одинаковых значений; то есть
любые 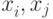 обладают тем свойством, что если
обладают тем свойством, что если 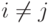 ,
то либо
,
то либо  , либо
, либо 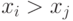 .
Ограничение
.
Ограничение 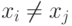 при
при 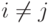 упрощает
анализ без потери общности, ибо и при наличии равных имен корректность
идей и алгоритмов не нарушается. Наша цель состоит в том, чтобы выяснить что-
нибудь относительно перестановки
упрощает
анализ без потери общности, ибо и при наличии равных имен корректность
идей и алгоритмов не нарушается. Наша цель состоит в том, чтобы выяснить что-
нибудь относительно перестановки 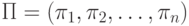 для которой
для которой  . В задаче полной
сортировки требуется полностью определить
. В задаче полной
сортировки требуется полностью определить  , хотя
обычно это делается неявно путем переразмещения имени в порядке возрастания. В
задачах частичной
сортировки требуется либо извлечь частичную
информацию о
, хотя
обычно это делается неявно путем переразмещения имени в порядке возрастания. В
задачах частичной
сортировки требуется либо извлечь частичную
информацию о  (например,
(например,  для нескольких
значений
для нескольких
значений  ), либо полностью определить
), либо полностью определить  по
некоторой заданной частичной информации о
ней (так обстоит дело при слиянии двух упорядоченных таблиц).
по
некоторой заданной частичной информации о
ней (так обстоит дело при слиянии двух упорядоченных таблиц).
При внутренней
сортировке решается задача полной сортировки для
случая достаточно малой таблицы, умещающейся непосредственно в адресной памяти. Внешняя
сортировка представляет собой задачу полной сортировки для случая
такой большой таблицы, что доступ к ней организован по частям, расположенным на
внешних запоминающих устройствах. Частичная сортировка - задачи выбора  -
наибольшего имени и слияния двух упорядоченных таблиц.
-
наибольшего имени и слияния двух упорядоченных таблиц.
Внутренняя сортировка
Существует по крайней мере пять широких классов алгоритмов внутренней сортировки.
- Вставка. На
 -м этапе
-м этапе  -е имя помещается на
надлежащее место между
-е имя помещается на
надлежащее место между  уже отсортированным именами:
уже отсортированным именами:
- Обмен. Два имени, расположение которых не соответствует порядку, меняются местами (обмен). Эти процедуры повторяются до тех пор, пока остаются такие пары.
- Выбор. На
 -м этапе из неотсортированных имен выбирается
-м этапе из неотсортированных имен выбирается  -е наибольшее (наименьшее) имя и помещается на соответствующее
место.
-е наибольшее (наименьшее) имя и помещается на соответствующее
место.
- Распределение. Имена распределяются по группам, и содержимое групп затем объединяется таким образом, чтобы частично отсортировать таблицу; процесс повторяется до тех пор, пока таблица не будет отсортирована полностью.
- Слияние. Таблица делится на подтаблицы, которые сортируются по отдельности и затем сливаются в одну.
Эти классы нельзя назвать ни взаимоисключающими, ни исчерпывающими: одни алгоритмы сортировки можно с полным основанием отнести более чем к одному классу (пузырьковую сортировку можно рассматривать и как выбор, и как обмен), а другие не укладываются ни в один из классов. Тем не менее, перечисленные пять классов достаточно удобны для классификации обсуждаемых алгоритмов сортировки.
Сосредоточим внимание на первых четырех классах алгоритмов сортировки. Алгоритмы, основанные на слиянии, приемлемы для внутренней сортировки, но более естественно рассматривать их как методы внешней сортировки.
В описываемых алгоритмах сортировки имена образуют последовательность,
которую будем обозначать  независимо от
возможных пересылок данных; таким образом, значением
независимо от
возможных пересылок данных; таким образом, значением  является
любое текущее имя в
является
любое текущее имя в  -й позиции последовательности. Многие
алгоритмы сортировки наиболее применимы к
массивам; в этом случае
-й позиции последовательности. Многие
алгоритмы сортировки наиболее применимы к
массивам; в этом случае  обозначает
обозначает  -й элемент
массива. Другие алгоритмы более приспособлены для работы со
связанными списками: здесь
-й элемент
массива. Другие алгоритмы более приспособлены для работы со
связанными списками: здесь  обозначает
обозначает  -й
элемент списка. Следующие обозначения используются для пересылок данных:
-й
элемент списка. Следующие обозначения используются для пересылок данных:
 значения
значения  и
и  меняются местами.
меняются местами.  значение
значение  присваивается имени
присваивается имени  .
.  значение имени
значение имени  присваивается
присваивается  .
.
Таким образом, операция 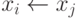 , которая
встречается в различных алгоритмах сортировки, временно нарушает
предположение о том, что никакие два имени не имеют одинаковых значений. Однако
это условие всегда обязательно восстанавливается.
, которая
встречается в различных алгоритмах сортировки, временно нарушает
предположение о том, что никакие два имени не имеют одинаковых значений. Однако
это условие всегда обязательно восстанавливается.
В каждом из рассматриваемых алгоритмов будем считать, что имена нужно
сортировать на месте. Другими словами, переразмещение имен должно происходить
внутри последовательности  ; при этом существуют
одна или две дополнительные ячейки, в которых временно
размещается значение имени. Ограничение "на месте" основано на
предположении,
будто число имен настолько велико, что во время сортировки не допускается
перенос
их в другую область памяти. Если в распоряжении имеется память, достаточная для
такого переноса, то некоторые из обсуждаемых алгоритмов можно значительно
ускорить. Эти рассмотрения заставляют нас в алгоритмах распределяющей
сортировки
и сортировки слиянием реализовать последовательность
; при этом существуют
одна или две дополнительные ячейки, в которых временно
размещается значение имени. Ограничение "на месте" основано на
предположении,
будто число имен настолько велико, что во время сортировки не допускается
перенос
их в другую область памяти. Если в распоряжении имеется память, достаточная для
такого переноса, то некоторые из обсуждаемых алгоритмов можно значительно
ускорить. Эти рассмотрения заставляют нас в алгоритмах распределяющей
сортировки
и сортировки слиянием реализовать последовательность  как связанный список.
как связанный список.
Вставка
Вставка - простейшая
сортировка вставками проходит через этапы 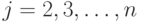 : на этапе
: на этапе  имя
имя  вставляется на свое правильное
место среди
вставляется на свое правильное
место среди 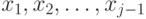 .
.

Рис. 14.1. Простая сортировка вставками, используемая на таблице из n = 5 имен. Пунктирные вертикальные линии разделяют уже отсортированную часть таблицы и еще не отсортированную
При вставке имя  временно размещается в
временно размещается в  , и
просматриваются имена
, и
просматриваются имена 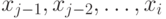 ; они
сравниваются с
; они
сравниваются с  и сдвигаются вправо, если обнаруживается, что
они больше
и сдвигаются вправо, если обнаруживается, что
они больше  . Имеется фиктивное имя
. Имеется фиктивное имя  , значение
которого
, значение
которого  служит для остановки просмотра слева. На рис.
14.1 работа этого алгоритма
проиллюстрирована на примере таблицы из пяти имен.
служит для остановки просмотра слева. На рис.
14.1 работа этого алгоритма
проиллюстрирована на примере таблицы из пяти имен.
Эффективность этого алгоритма, как и большинства алгоритмов сортировки,
зависит
от числа сравнений имен и числа пересылок данных, осуществляемых в трех
случаях :
худшем, среднем (в предположении, что все  ! перестановок
равновероятны) и лучшем.
! перестановок
равновероятны) и лучшем.