Рекуррентные соотношения
Другой метод доказательства
В предыдущем разделе непосредственно установлена связь между задачей
Фибоначчи и комбинаторной задачей. Эту связь можно установить и иначе,
непосредственно доказав, что число 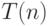 решений комбинаторной
задачи удовлетворяет тому же рекуррентному соотношению
решений комбинаторной
задачи удовлетворяет тому же рекуррентному соотношению
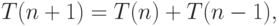 |
( 7.5) |
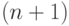 -последовательность
нулей и единиц, удовлетворяющую условию, что никакие две
единицы не идут подряд. Она может оканчиваться или на 0, или на 1. Если она
оканчивается на 0, то, отбросив его, получим
-последовательность
нулей и единиц, удовлетворяющую условию, что никакие две
единицы не идут подряд. Она может оканчиваться или на 0, или на 1. Если она
оканчивается на 0, то, отбросив его, получим  -последовательность, удовлетворяющую нашему условию. Если взять
любую
-последовательность, удовлетворяющую нашему условию. Если взять
любую  - последовательность нулей и единиц, в которой подряд не
идут две единицы, и приписать к ней нуль, то получим
- последовательность нулей и единиц, в которой подряд не
идут две единицы, и приписать к ней нуль, то получим 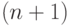 -последовательность с тем
же свойством. Таким образом доказано, что число
последовательностей, оканчивающихся на нуль, равно
-последовательность с тем
же свойством. Таким образом доказано, что число
последовательностей, оканчивающихся на нуль, равно 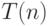 .
.Пусть теперь последовательность оканчивается на 1. Так как двух единиц
подряд быть не может, то перед этой единицей стоит нуль. Иными словами,
последовательность оканчивается на 01. Остающаяся же после отбрасывания 0 и 1 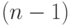 -последовательность может быть любой, лишь бы в ней не шли
подряд две единицы. Поэтому число последовательностей, оканчивающихся единицей, равно
-последовательность может быть любой, лишь бы в ней не шли
подряд две единицы. Поэтому число последовательностей, оканчивающихся единицей, равно 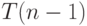 . Но каждая последовательность оканчивается или на 0, или на 1. В
силу правила суммы получаем, что
. Но каждая последовательность оканчивается или на 0, или на 1. В
силу правила суммы получаем, что 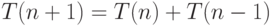 .
.
Таким образом, получено то же самое рекуррентное соотношение. Отсюда еще
не вытекает, что числа 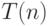 и
и  совпадают.
совпадают.
Процесс последовательных разбиений
Для решения комбинаторных задач часто применяют метод, использованный в предыдущем пункте: устанавливают для данной задачи рекуррентное соотношение и показывают, что оно совпадает с рекуррентным соотношением для другой задачи, решение которой нам уже известно. Если при этом совпадают и начальные члены последовательностей в достаточном числе, то обе задачи имеют одинаковые решения.
Применим описанный прием для решения следующей задачи.
Пусть дано некоторое множество из  предметов, стоящих в
определенном порядке. Разобьем это множество на две
непустые части так, чтобы одна из этих частей лежала левее второй (то есть,
скажем, одна часть состоит из элементов от первого до
предметов, стоящих в
определенном порядке. Разобьем это множество на две
непустые части так, чтобы одна из этих частей лежала левее второй (то есть,
скажем, одна часть состоит из элементов от первого до  - го, а
вторая - из элементов от
- го, а
вторая - из элементов от 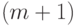 -го до
-го до  -го).
После этого каждую из частей таким же образом разобьем на две непустые
части (если одна из частей состоит уже из одного предмета, она не подвергается
дальнейшим разбиениям). Этот процесс продолжается до тех пор, пока не получим
части, состоящие из одного предмета каждая. Сколько существует таких процессов
разбиения (два процесса считаются различными, если хотя бы на одном шагу они
приводят к разным результатам)?
-го).
После этого каждую из частей таким же образом разобьем на две непустые
части (если одна из частей состоит уже из одного предмета, она не подвергается
дальнейшим разбиениям). Этот процесс продолжается до тех пор, пока не получим
части, состоящие из одного предмета каждая. Сколько существует таких процессов
разбиения (два процесса считаются различными, если хотя бы на одном шагу они
приводят к разным результатам)?
Обозначим число способов разбиения для множества из  предметов через
предметов через  . На первом шагу это множество может быть
разбито
. На первом шагу это множество может быть
разбито  способами (первая часть может содержать один предмет,
два предмета,…,
способами (первая часть может содержать один предмет,
два предмета,…,  предметов). В соответствии с этим множество всех
процессов разбиений распадается
на
предметов). В соответствии с этим множество всех
процессов разбиений распадается
на  классов - в
классов - в  - класс входят процессы, при
которых первая часть состоит из
- класс входят процессы, при
которых первая часть состоит из  предметов.
предметов.
Подсчитаем число процессов в  -м классе. В первой части
содержится
-м классе. В первой части
содержится  элементов. Поэтому ее можно разбивать далее
элементов. Поэтому ее можно разбивать далее 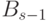 различными процессами. Вторая же часть содержит
различными процессами. Вторая же часть содержит  элементов, и ее можно разбивать далее
элементов, и ее можно разбивать далее 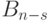 процессами. По правилу произведения получаем, что
процессами. По правилу произведения получаем, что  - класс
состоит из
- класс
состоит из  различных процессов. По правилу
суммы отсюда вытекает, что
различных процессов. По правилу
суммы отсюда вытекает, что
 |
( 7.6) |
 . Двоичный поиск,
поиск делением пополам. Поиском по числам
Фибоначчи называется поиск, основанный на том, что область поиска
делится в точках, являющихся числами Фибоначчи.
. Двоичный поиск,
поиск делением пополам. Поиском по числам
Фибоначчи называется поиск, основанный на том, что область поиска
делится в точках, являющихся числами Фибоначчи.Задача: "Затруднение мажордома"
Бывают комбинаторные задачи, в которых приходится составлять не одно
рекуррентное соотношение, а систему соотношений, связывающую несколько
последовательностей. Эти соотношения выражают 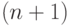 -у члены
последовательностей через предыдущие члены не только данной, но и
остальных последовательностей.
-у члены
последовательностей через предыдущие члены не только данной, но и
остальных последовательностей.
Задача: "Затруднение мажордома". Однажды мажордом короля Артура обнаружил, что к обеду за круглым столом приглашено 6 пар враждующих рыцарей. Сколькими способами можно рассадить их так, чтобы никакие два врага не сидели рядом?
Если мы найдем какой-то способ рассадки рыцарей, то, пересаживая их по кругу, получим еще 11 способов. Мы не будем сейчас считать различными способы, получающиеся друг из друга такой циклической пересадкой.
Введем следующие обозначения. Пусть число рыцарей равно  .
Через
.
Через 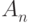 обозначим число способов рассадки, при которых
никакие два врага не сидят рядом.
Через
обозначим число способов рассадки, при которых
никакие два врага не сидят рядом.
Через  обозначим число способов, при которых рядом сидит ровно
одна пара врагов, и через
обозначим число способов, при которых рядом сидит ровно
одна пара врагов, и через  - число способов, при которых есть ровно две пары
враждующих соседей.
- число способов, при которых есть ровно две пары
враждующих соседей.
Выведем сначала формулу, выражающую 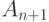 через
через  . Пусть
. Пусть  пар рыцарей посажены так,
что никакие два врага не сидят рядом. Мы будем считать,
что все враждующие пары рыцарей занумерованы. Попросим встать из-за стола пару
рыцарей с номером
пар рыцарей посажены так,
что никакие два врага не сидят рядом. Мы будем считать,
что все враждующие пары рыцарей занумерованы. Попросим встать из-за стола пару
рыцарей с номером  . Тогда возможны три случая: среди
оставшихся за столом нет одной пары соседей-
врагов, есть одна такая пара и есть две такие пары (ушедшие рыцари могли
разделять эти пары). Мы считаем, что
. Тогда возможны три случая: среди
оставшихся за столом нет одной пары соседей-
врагов, есть одна такая пара и есть две такие пары (ушедшие рыцари могли
разделять эти пары). Мы считаем, что  . При
. При 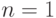 последующие рассуждения теряют силу.
последующие рассуждения теряют силу.
Выясним теперь, сколькими способами можно снова посадить ушедших рыцарей за стол так, чтобы после этого не было одной пары соседей-врагов.
Проще всего посадить их, если за столом рядом сидят две пары врагов. В этом
случае один из вновь пришедших садится между рыцарями первой пары, а другой –
между рыцарями второй пары. Это можно сделать двумя способами. Но так как число
способов рассадки  рыцарей, при которых две пары соседей
оказались врагами, равно
рыцарей, при которых две пары соседей
оказались врагами, равно  , то всего получилось
, то всего получилось 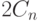 способов.
способов.
Пусть теперь рядом сидит только одна пара врагов. Один из вернувшихся
должен сесть между ними. Тогда за столом окажутся 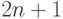 рыцарей,
между которыми есть
рыцарей,
между которыми есть 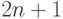 мест. Из них два места - рядом с
только что севшим гостем – запретны для второго
рыцаря, и ему остается
мест. Из них два места - рядом с
только что севшим гостем – запретны для второго
рыцаря, и ему остается 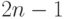 мест. Так как первым может войти
любой из двух вышедших рыцарей, то получается
мест. Так как первым может войти
любой из двух вышедших рыцарей, то получается  способов рассадки. Но число случаев, когда
способов рассадки. Но число случаев, когда  рыцарей сели так, чтобы ровно одна пара врагов оказалась
соседями, ровно
рыцарей сели так, чтобы ровно одна пара врагов оказалась
соседями, ровно  . Поэтому мы получаем
. Поэтому мы получаем  способов посадить гостей требуемым образом.
способов посадить гостей требуемым образом.
Наконец, пусть никакие два врага не сидели рядом. В этом случае первый
рыцарь садится между любыми двумя гостями - это он может сделать  способами. После этого для его врага останется
способами. После этого для его врага останется 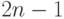 мест - он может занять любое место, кроме двух мест, соседних с
только что севшим рыцарем. Таким образом, если
мест - он может занять любое место, кроме двух мест, соседних с
только что севшим рыцарем. Таким образом, если  рыцарей уже сидели нужным
образом, то вернувшихся гостей можно посадить
рыцарей уже сидели нужным
образом, то вернувшихся гостей можно посадить  способами. Как уже отмечалось, разработанными случаями исчерпываются все
возможности. Поэтому имеет место рекуррентное соотношение
способами. Как уже отмечалось, разработанными случаями исчерпываются все
возможности. Поэтому имеет место рекуррентное соотношение
 |
( 7.7) |
Этого соотношения пока недостаточно, чтобы найти 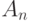 для всех значений
для всех значений  . Надо еще узнать, как выражаются
. Надо еще узнать, как выражаются  через
через 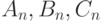 .
.
Предположим, что среди 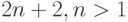 рыцарей оказалась ровно
одна пара врагов-соседей. Мы знаем, что это может
произойти в
рыцарей оказалась ровно
одна пара врагов-соседей. Мы знаем, что это может
произойти в 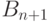 случаях. Во избежание ссоры попросим их
удалиться из-за стола. Тогда останется
случаях. Во избежание ссоры попросим их
удалиться из-за стола. Тогда останется  рыцарей, причем
возможно одно из двух: либо среди оставшихся нет врагов-соседей,
либо есть ровно одна пара таких врагов - до ухода покинувших зал они сидели
по обе стороны от них и теперь оказались рядом. Во втором случае ушедших можно
посадить обратно только на старое место - иначе появится вторая пара враждующих
соседей. Но так как
рыцарей, причем
возможно одно из двух: либо среди оставшихся нет врагов-соседей,
либо есть ровно одна пара таких врагов - до ухода покинувших зал они сидели
по обе стороны от них и теперь оказались рядом. Во втором случае ушедших можно
посадить обратно только на старое место - иначе появится вторая пара враждующих
соседей. Но так как  рыцарей можно посадить
рыцарей можно посадить  способами
так, чтобы была только одна пара враждующих соседей, то мы получаем
способами
так, чтобы была только одна пара враждующих соседей, то мы получаем  вариантов (возвратившихся рыцарей можно поменять местами). В
первом же случае можно посадить ушедших между любыми двумя рыцарями, то есть
вариантов (возвратившихся рыцарей можно поменять местами). В
первом же случае можно посадить ушедших между любыми двумя рыцарями, то есть  способами, а так как их еще можно поменять местами, то получится
способами, а так как их еще можно поменять местами, то получится 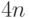 способов. Комбинируя их со всеми способами посадки
способов. Комбинируя их со всеми способами посадки  пар рыцарей, при которых нет соседей врагов, получаем
пар рыцарей, при которых нет соседей врагов, получаем 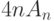 способов. Наконец, номер ушедшей и вернувшейся пары рыцарей
мог быть любым от 1 до
способов. Наконец, номер ушедшей и вернувшейся пары рыцарей
мог быть любым от 1 до  . Отсюда вытекает, что рекуррентное соотношение для
. Отсюда вытекает, что рекуррентное соотношение для 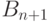 имеет вид
имеет вид
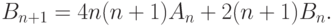 |
( 7.8) |
Наконец, разберем случай, когда среди 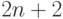 рыцарей было две
пары врагов-соседей. Номера этих пар можно выбрать
рыцарей было две
пары врагов-соседей. Номера этих пар можно выбрать 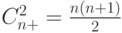 способами. Заменим каждую пару одним новым рыцарем, причем будем
считать новых двух рыцарей врагами. Тогда за столом будут сидеть
способами. Заменим каждую пару одним новым рыцарем, причем будем
считать новых двух рыцарей врагами. Тогда за столом будут сидеть  рыцарей, причем среди них либо не будет ни одной пары врагов-соседей (если
новые рыцари не сидят рядом), либо только одна такая пара.
рыцарей, причем среди них либо не будет ни одной пары врагов-соседей (если
новые рыцари не сидят рядом), либо только одна такая пара.
Первый вариант может быть в 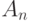 случаях. Вернуться к исходной
компании мы можем 4 способами благодаря возможности изменить порядок рыцарей в каждой
паре. Поэтому первый вариант приводит к
случаях. Вернуться к исходной
компании мы можем 4 способами благодаря возможности изменить порядок рыцарей в каждой
паре. Поэтому первый вариант приводит к 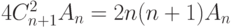 способами.
способами.
Второй же вариант может быть в 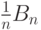 случаях. Имеется
случаях. Имеется  случаев, когда какая-нибудь пара врагов сидит рядом. Если указать, какая именно пара
должна сидеть рядом, получим в
случаев, когда какая-нибудь пара врагов сидит рядом. Если указать, какая именно пара
должна сидеть рядом, получим в  раз меньше случаев.
раз меньше случаев.
Здесь тоже можно вернуться к исходной компании 4 способами, и мы получаем
всего 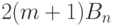 способов. Отсюда вытекает, что при
способов. Отсюда вытекает, что при 
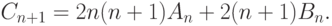 |
( 7.9) |
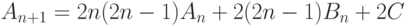 |
( 7.10) |
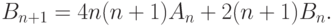 |
( 7.11) |
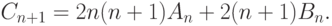 |
( 7.12) |
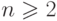 . Но простой подсчет показывает,
что
. Но простой подсчет показывает,
что 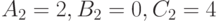 . Поэтому из соотношений 7.10-7.12
вытекает, что
. Поэтому из соотношений 7.10-7.12
вытекает, что  . Продолжая далее,
находим, что гостей можно посадить за стол требуемым образом
. Продолжая далее,
находим, что гостей можно посадить за стол требуемым образом 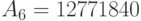 способами.
способами.