Эксперименты с билинейными автоматами по распознаванию состояний
Установочные последовательности
Условия существования такой последовательности даются следующей теоремой.
Теорема 21.4. Для того чтобы последовательность 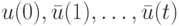 была УП для БА
была УП для БА  , необходимо и достаточно, чтобы для каждого ненулевого состояния
, необходимо и достаточно, чтобы для каждого ненулевого состояния 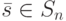 выполнялось по крайней мере одно из двух условий:
выполнялось по крайней мере одно из двух условий:
-
![\wedge_{d=0}^t[C+J(\bar u(d))] \prod_{i=0}^{d-1}[A+I(\bar u(d-i-1))]\bar s \ne 0](/sites/default/files/tex_cache/6e74b6e378601f7597eb5e650c581442.png) ;
; ![\prod_{i=0}^{t}[A+I(\bar u(t-i))]\bar s=[0]](/sites/default/files/tex_cache/e8c394dee755a708454fff63522c7016.png)
Здесь знак  означает дизъюнкцию (конъюнкцию) выражений, стоящих за этим знаком и получаемых при изменении индекса
означает дизъюнкцию (конъюнкцию) выражений, стоящих за этим знаком и получаемых при изменении индекса  от 0 до
от 0 до  . Условимся о следующем: если при вычислении
. Условимся о следующем: если при вычислении  и
и  окажется, что
окажется, что 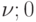 при некоторых
при некоторых  и
и  , то в соответствующем выражении сомножители
, то в соответствующем выражении сомножители ![[A+I(\bar u(\nu))]](/sites/default/files/tex_cache/855e67b59403abbc7760ee18411dcf59.png) и
и ![[C+J(\bar u(\nu))]](/sites/default/files/tex_cache/e59b8f4b63fb9d1db65561368f0b4ef0.png) полагаются равными единичной матрице.
полагаются равными единичной матрице.
Доказательство. Применительно к БА  определение 1.2 УП принимает следующий вид: последовательность
определение 1.2 УП принимает следующий вид: последовательность 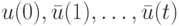 называется УП, если
называется УП, если
![\forall \bar s_1, \bar s_2, \in S_n, \wedge_{d=0}^t\{[C+J(\bar u(d))]\prod_{i=0}^{d-1}[A+I(\bar u(d-i-1))]s_1+\dots\\
\dots +[C+J(\bar u(d))]B\bar u(d-1)+D\bar u(d)=[C+J(\bar u(d))]\prod_{i=0}^{d-1}[A+I(d-i-1)]\bar s_2+ \dots\\
\dots =[C+j(\bar u(d))]B\bar u(0)+ \dots + [A+I(u(t))]B\bar u(t-1)+B\bar u(t)=\\
=\prod_{i=0}^{t-1}[A+I(\bar u(t-i-1))]B\bar u(0)+\dots +[A+I(u(t))]B\bar u(t-1)+B\bar u(t)=\\
=\prod_{i=0}^{t-1}[A+I(\bar u(t-i))]\bar s_2+\prod_{i=0}^{t-1}[A+I(\bar u(t-i-1))]B\bar u(0)+\dots +[A+I(\bar u(t))]B\bar u(t-1)+B\bar u(t) \right ]](/sites/default/files/tex_cache/83353aedea4f928b34d8b6b42d352f8a.png)
Преобразуем каждое в отдельности равенство, стоящее до и после знака импликации, перенеся все в левые их части и осуществив соответствующие сокращения, в результате чего получим
![\forall \bar s_1, \bar s_2 \in S_n, [\wedge_{d=0}^t[C+J(\bar u(d))]\prod_{i=0}^t[A+I(d-i-1)](\bar s_1-\bar s_2)=[0]] \to\\
\to \prod_{i=0}^t[A+I(\bar u(t-i))](\bar s_1- \bar s_2)=[0]](/sites/default/files/tex_cache/841d58f3150fd864436789941792c8d8.png)
Поскольку  и
и  - произвольные не совпадающие между собой состояния из
- произвольные не совпадающие между собой состояния из 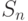 , то и состояние
, то и состояние 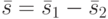 также может быть любым ненулевым состоянием из
также может быть любым ненулевым состоянием из 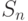 . Отсюда следует, что последний предикат эквивалентен предикату
. Отсюда следует, что последний предикат эквивалентен предикату
![\forall \bar s \ne [0]
[\wedge_{d=0}^t[C+J(\bar u(d))] \prod_{i=0}^{d-1}[A+I(\bar u(d-i-1))]\bar s=[0] \to \prod_{i=0}^t[A+I(\bar u(t-i))]\bar s=[0]](/sites/default/files/tex_cache/7154dc2883264b3727c9051537f7f925.png)
Поскольку 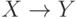 эквивалентно
эквивалентно  , то последний предикат эквивалентен следующему предикату
, то последний предикат эквивалентен следующему предикату
![\forall \bar s \ne [0]
[\vee_{d=0}^t[C+J(\bar u(d))]\prod_{i=0}^{d-1}[A+I(\bar u(d-i-1))]\bar \ne [0]] \vee
\vee \prod_{i=0}t[A+I(\bar u(t-i))]\bar s=[0]](/sites/default/files/tex_cache/f5f8f465b2614e1e3b5434e7b4612c6f.png)
Из этого предиката и следует справедливость теоремы.
Проиллюстрируем предложенный метод на примере БА над полем  , у которого
, у которого  , а характеристические матрицы таковы:
, а характеристические матрицы таковы:
![A=
\left [
\begin {matrix}
1&0&0\\
0&1&0\\
0&0&1
\end {matrix}
\right ] ,
B=
\left [
\begin {matrix}
1&0\\
0&1\\
1&0
\end {matrix}
\right ],
F_1=
\left [
\begin {matrix}
0&0&1\\
0&1&0\\
0&0&0
\end {matrix}
\right ],
F_2=
\left [
\begin {matrix}
0&0&1\\
0&0&0\\
1&0&1
\end {matrix}
\right ] ,\\
C=
\left [
\begin {matrix}
0&0&1\\
0&1&1
\end {matrix}
\right ],
D=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ] ,
G_1=
\left [
\begin {matrix}
1&0&1\\
0&1&1
\end {matrix}
\right ],
G_2=
\left [
\begin {matrix}
0&1&1\\
1&0&1
\end {matrix}
\right ]](/sites/default/files/tex_cache/2160ef50159dd1a90454c3c5383c5fb0.png)
Первое условие теоремы 21.4 при 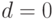 порождает систему уравнений
порождает систему уравнений
![[C+J(\bar u(0))]\bar s=
\left [
\begin {matrix}
u_1(0)& u_2(0)& u_1(0)+u_2(0)+1\\
u_2(0)& u_1(0)+1& u_1(0)+u_2(0)+1
\end {matrix}
\right ] *
\left [
\begin {matrix}
s_1\\
s_2\\
s_3
\end {matrix}
\right ]=[0]](/sites/default/files/tex_cache/e584a2d8bfb45a05b60f0ef470c1a483.png)
Рассмотрим теперь все возможные векторы ![\bar u(0):[0,0]' [1,0]', [1,0]', [1,1]'](/sites/default/files/tex_cache/180c6f79966020f7b7dcf0229db69147.png) . Их подстановка в выписанную нелинейную систему порождает четыре следующих системы:
. Их подстановка в выписанную нелинейную систему порождает четыре следующих системы:
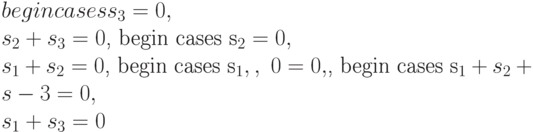
Каждая из этих систем относительно неизвестных 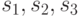 имеет не единственное решение, и поэтому условие 1 теоремы 21.4 для всех входных последовательностей длины 1 не выполняется. Перейдем теперь к проверке условия 2 той же теоремы, которое при
имеет не единственное решение, и поэтому условие 1 теоремы 21.4 для всех входных последовательностей длины 1 не выполняется. Перейдем теперь к проверке условия 2 той же теоремы, которое при 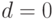 порождает систему
порождает систему
![[A+I(\bar u(0))]\bar s=
\left [
\begin {matrix}
1&0&u_i(0)+u_2(0)\\
0&u_1(0)+1&0\\
u_2(0)&0&u_2(0)+1
\end {matrix}
\right ]*
\left [
\begin {matrix}
s_1\\
s_2\\
s_3
\end {matrix}
\right ]=[0]](/sites/default/files/tex_cache/7cece0c4a4547007e545bef0e4f6c779.png)
Легко проверить, что эта система имеет единственное (нулевое) решение при любом  , т. е. условие 2 также не выполняется. Поэтому перейдем к поиску УП длины 2, полагая
, т. е. условие 2 также не выполняется. Поэтому перейдем к поиску УП длины 2, полагая  .
.
Условие 1 теоремы 21.4 порождает следующую систему уравнений:
![begin {cases}
[C+J(\bar u(0))]\bar s=[0],\\
{C+J(\bar u(1))][A+I(\bar u(0))]\bar s=[0]
\end {cases}](/sites/default/files/tex_cache/a83046704756c3b264990719e6908ee1.png)
В координатной записи эта же система имеет следующий вид:
![\left [
\begin {matrix}
u_1(0)&u_2(0)&u_1(0)+u_2(0)+1\\
u_2(0)&u_1(0)+1&u_1(0)+u_2(0)+1
\end {matrix}
\right ]*
\left [
\begin {matrix}
s_1\\
s_2\\
s_3
\end {matrix}
\right ]=[0],\\
\left [
\begin {matrix}
[u_1(1)+u_2(1)+1]*&u_2(1)[u_1(0)+1]&u_1(1)[u_1(0)+u_2(0)]+\\
*u_2(0)+u_1(1)&&+u_1(1)+u_2(1)+1][u_2(0)+1]\\
[u_1(1)+u_2(1)+1]*&[u_1(1)+1]*&u_2(1)[u_1(0)+u_2(0)]+\\
*u_2(0)+u_2(01)&*[u_1(0)+1]&+[u_1(1)+u_2(1)+1][u_2(0)+1]
\end {matrix}
\right ]*
\left [
\begin {matrix}
s_1\\
s_2\\
s_3
\end {matrix}
\right ]=[0]](/sites/default/files/tex_cache/5b65b95c7c8fb0bff6bdcd084e11352a.png)
Теперь необходимо рассмотреть все возможные пары векторов 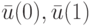 и, подставляя их в выписанную выше систему, получить множество систем линейных уравнений относительно неизвестных
и, подставляя их в выписанную выше систему, получить множество систем линейных уравнений относительно неизвестных 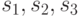 . Вычисления показывают, что, например, для пар входных векторов
. Вычисления показывают, что, например, для пар входных векторов ![\bar u(0)=[1,1]', \bar u(1)=[0,0}'](/sites/default/files/tex_cache/44dc2f6654524720726bcee7782a6e98.png) и
и ![\bar u(0)=[0,0]', \bar u(1)=[1,0]'](/sites/default/files/tex_cache/6c8432f39b1ca2f1ccf71fc63a9331b1.png) первая подсистема
первая подсистема ![[C+J(\bar u(0))]\bar s=[0]](/sites/default/files/tex_cache/fffca6882f08cf39ade3013607495b8f.png) имеет ненулевое решение (
имеет ненулевое решение ( ![\bar s=[1,0,1]'](/sites/default/files/tex_cache/586ff395cdffc4ec5453fd56fa55c038.png) и
и ![\bar s=[1,0,0]'](/sites/default/files/tex_cache/cfe1f0f673c9dc36906252f4c586a66b.png) соответственно), а вторая подсистема для этих же пар входных векторов имеет единственное (нулевое) решение. Последний факт означает, что условие 1 теоремы выполняется, следовательно, обе приведенные входные последовательности являются для рассматриваемого БА установочными. Заметим, что этот БА имеет и другие УП длины 2, которые находятся аналогично.
соответственно), а вторая подсистема для этих же пар входных векторов имеет единственное (нулевое) решение. Последний факт означает, что условие 1 теоремы выполняется, следовательно, обе приведенные входные последовательности являются для рассматриваемого БА установочными. Заметим, что этот БА имеет и другие УП длины 2, которые находятся аналогично.
Для подтверждения сказанного, в приведенной таблице показаны реакции рассматриваемого БА на две найденные входные последовательности и соответствующие конечные состояния. Состояния БА в таблице закодированы в виде десятичного эквивалента двоичного представления вектора-состояния. Так, например, состояние ![\bar s=[1,0,0]'](/sites/default/files/tex_cache/cfe1f0f673c9dc36906252f4c586a66b.png) закодировано числом 4, состояние
закодировано числом 4, состояние ![\bar s=[1,0,1]'](/sites/default/files/tex_cache/586ff395cdffc4ec5453fd56fa55c038.png) - числом 5 и т. д.
- числом 5 и т. д.
| Входное слово 3, 0 | Входное слово 0, 2 | |||
|---|---|---|---|---|
| Начальное состояние | Реакция БА | Конечное состояние | Реакция БА | Конечное состояние |
| 0 | 3, 2 | 7 | 0, 2 | 5 |
| 1 | 0, 2 | 7 | 3, 2 | 0 |
| 2 | 1, 2 | 7 | 1, 2 | 5 |
| 3 | 2, 2 | 7 | 2, 2 | 0 |
| 4 | 0, 1 | 2 | 0, 0 | 1 |
| 5 | 3, 1 | 2 | 3, 0 | 5 |
| 6 | 2, 1 | 2 | 1, 0 | 1 |
| 7 | 1, 1 | 2 | 2, 0 | 4 |
Аналогичная кодировка в таблице принята для входных и выходных векторов. Так, УП ![[0,0]', [1,0]'](/sites/default/files/tex_cache/efe5a9c58d3d670f911a5dc205bf005c.png) закодирована как последовательность 0, 2; а УП
закодирована как последовательность 0, 2; а УП ![[1,1]', [0,0]'](/sites/default/files/tex_cache/4dcdb242a3ca4320b86ba208c64171e2.png) - как последовательность 3, 0.
- как последовательность 3, 0.
Диагностические последовательности
Условия существования такой последовательности даются следующей теоремой.
Теорема 21.5. Для того чтобы последовательность 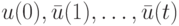 была ДП для БА
была ДП для БА  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
![rank \left [
\begin {matrix}
C+J(\bar u(0)\\
[C+J(\bar u(1))][A+I(\bar u(0))]\\
………………………………….\\
[C+J(\bar u(t))]\prod_{i=0}^{t-1}[A+I(\bar u(t-i-1))]
\end {matrix}
\right ]=n, \ \mbox {где} \ {n} \ \mbox {размерность БА}](/sites/default/files/tex_cache/c7835976fcec1c03fe31ecf5226678ea.png)
Доказательство. Применительно к БА определение 1.3 ДП принимает следующий вид: последовательность 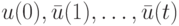 называется ДП, если
называется ДП, если
![\forall \bar s_1, \bar s_2 \in S_n \wedge_{d=0}^{t} \left \{[C+J(\bar u(d))]\prod_{i=0}^{d-1}[A+I(\bar u(d-i-1))]\bar s_1+](/sites/default/files/tex_cache/7ea2b8c0733dbd7bbdb9ed6ed58168d0.png)
![\dots, [C+J(\bar u(d))]B\bar u(d-1)+D\bar u(d)=[C+J(\bar u(d))]\prod_{i=0}^{d-1}[A+I(\bar u(d-i-1))]\bar s_2+](/sites/default/files/tex_cache/c917bf6ccdc1165019d63411e337212c.png)
![\dots +[C+J(\bar u(d))]B\bar u(d-1)+D\bar u(d) \right \} \to \bar s_1=\bar s_2](/sites/default/files/tex_cache/84ff3471df77bc804485f9a25ab91f4a.png)
Выполнив преобразование так же, как это делалось в предыдущем доказательстве, получим предикат
![\forall \bar s_1, s_2 \in S_n \wedge_{d=0}^{t} \left \{[C+J(\bar u(d))]\prod_{i=0}^{d-1}[A+I (\bar u(d-i-1))](\bar s_1-\bar s_2)=0] \right \} \to \bar s_1=\bar s_2](/sites/default/files/tex_cache/666cb961ce15adc5d8d501dd868e880f.png)
Если последовательность 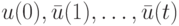 является для БА диагностической, то это означает, что знание реакции БА на нее позволяет однозначно найти ее начальное состояние. Выходы БА на ДП, используя (21.4), можно представить как функции от начального состояния
является для БА диагностической, то это означает, что знание реакции БА на нее позволяет однозначно найти ее начальное состояние. Выходы БА на ДП, используя (21.4), можно представить как функции от начального состояния  :
:
![\bar y(0)=[C+J(\bar u(0))]\bar s(0)+D\bar u(0),\\
\bar y(1)=[C+J(\bar u(1))][A+I(\bar u (1))]\bar s(0)+[C+J(\bar u(1))]B\bar u(0)+D\bar u(1),\\
………………………………….\\
\bar y(t)=[C+J(\bar u(t))]\prod_{i=0}^{t-1}[A+I(\bar u(t-i-1))]\bar s(0)+ \dots +D\bar u(t)](/sites/default/files/tex_cache/62d8990b0efef723a67d3e16d5d5d9e1.png)
Поскольку ДП 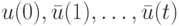 и реакция БА на нее известны, выписанные соотношения можно представить в виде
и реакция БА на нее известны, выписанные соотношения можно представить в виде
![[C+J(\bar u(0))]\bar s(0)= Ф_0(\bar u(0)),\\
[C+J(\bar u(1))][A+I(\bar u(0))]\bar s(0)= Ф_1(\bar u(0), \bar u(1)),\\
………………………………………………………\\
[C+J(\bar u(t))] \prod_{i=0}^{i-1}[A+I(\bar u(t-i-1))]\bar s(0)= Ф_t(\bar u(0), \dots, \bar u(t)))](/sites/default/files/tex_cache/398f1183348bf49e9c819b9334586e11.png)
где 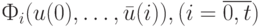 - некоторые значения из поля
- некоторые значения из поля  .
.
Выписанную совокупность соотношений можно интерпретировать как систему линейных уравнений относительно неизвестных 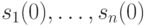 , являющихся координатами вектора-состояния
, являющихся координатами вектора-состояния  . Однозначность восстановления начального состояния
. Однозначность восстановления начального состояния  по наблюдаемой реакции
по наблюдаемой реакции 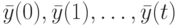 при известной входной последовательности
при известной входной последовательности 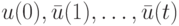 означает, что представленная система линейных уравнений должна иметь единственное решение. Из [33] известно, что для этого необходимо и достаточно, чтобы ранг этой системы был равен числу ее неизвестных. Отсюда и следует справедливость теоремы.
означает, что представленная система линейных уравнений должна иметь единственное решение. Из [33] известно, что для этого необходимо и достаточно, чтобы ранг этой системы был равен числу ее неизвестных. Отсюда и следует справедливость теоремы.
Опишем теперь метод нахождения ДП для заданного БА, основанный на теореме 21.5. Метод состоит в переборе всевозможных входных слов 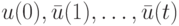 последовательно для
последовательно для 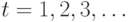 и вычислении для очередного проверяемого слова ранга матрицы, фигурирующей в теореме 21.5. Если этот ранг окажется равным n, то проверяемое входное слово является искомой ДП. В противном случае указанный процесс продолжается далее до тех пор, пока значение параметра
и вычислении для очередного проверяемого слова ранга матрицы, фигурирующей в теореме 21.5. Если этот ранг окажется равным n, то проверяемое входное слово является искомой ДП. В противном случае указанный процесс продолжается далее до тех пор, пока значение параметра  не достигнет своего предельного значения, равного верхней границе длины минимальной ДП для рассматриваемого БА. Если и при этом значении
не достигнет своего предельного значения, равного верхней границе длины минимальной ДП для рассматриваемого БА. Если и при этом значении  ДП не будет найдена, то для рассматриваемого БА ее не существует. Проиллюстрируем этот метод на примере БА, для которого выше осуществлялся поиск УП. Для этого БА приведем некоторые "составляющие" матрицы в условиях теоремы 21.5:
ДП не будет найдена, то для рассматриваемого БА ее не существует. Проиллюстрируем этот метод на примере БА, для которого выше осуществлялся поиск УП. Для этого БА приведем некоторые "составляющие" матрицы в условиях теоремы 21.5:
![[C+J(\bar u(0))]= \left [
\begin {matrix}
u_1(0)&u_2(0)&u_1(0)+u_2(0)+1\\
u_2(0)&U_1(0)+1& u_1(0)+u_2(0)+1
\end {matrix}
\right ],\\
[C+J(\bar u(0))][A+I(\bar u(0))]=
\left [
\begin {matrix}
[u_1(1)+u_2(1)]*u_2(0)+u_1(1)& u_2(1)[u_1(0)+1]&u_1(1)[u_1(0)+u_2(0)]+[u_1(1)+u_2(1)+1][u_2(0)+1]\\
[u_1(1)+u_2(1)]*u_2(0)+u_1(1)&[u_1(1)+1][u_1(0)+1]&u_2(1)[u_1(0)+u_2(0)]+[u_1(1)+u_2(1)+1][u_2(0)+1]
\end {matrix}
\right ]](/sites/default/files/tex_cache/18cb19e788563a6d468cb39e7ccbf16e.png)
Размерность матрицы ![[C+J(\bar u(0))]](/sites/default/files/tex_cache/766a82081d0a803bbc3bbedb8f1f4af8.png) равна
равна  , следовательно, ее ранг не может превышать 2. Но тогда, поскольку для рассматриваемой БС
, следовательно, ее ранг не может превышать 2. Но тогда, поскольку для рассматриваемой БС 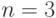 , условие теоремы 21.5 при
, условие теоремы 21.5 при 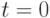 не может быть выполнено. В связи с этим перейдем к перебору всевозможных входных слов длины 2 (полагая
не может быть выполнено. В связи с этим перейдем к перебору всевозможных входных слов длины 2 (полагая 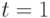 ). Рассмотрим, например, входное слово
). Рассмотрим, например, входное слово 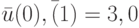 . Для него матрица из условия теоремы 21.5 имеет вид
. Для него матрица из условия теоремы 21.5 имеет вид
![\left [
\begin {matrix}
C+J(\bat u(0))\\
[C+J(\bar u(0))][A+I(\bar u(0))]
\end {matrix}
\right ]=
\left [
\begin {matrix}
1&0&0\\
1&0&0\\
1&1&1\\
1&0&1
\end {matrix}
\right ]](/sites/default/files/tex_cache/a49026b5dca2d5a361ff0f9f4b1df265.png)
Поскольку ранг этой матрицы равен 3, проверяемое слово 3, 0 есть ДП. В этом можно убедиться по данным, приведенным в таблице. Для другого входного слова 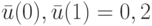 та же матрица из условий теоремы равна
та же матрица из условий теоремы равна
![\left [
\begin {matrix}
0&0&1\\
0&1&1\\
1&0&0\\
0&0&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/fbe1c7ff0a14930100f166a0ecafe111.png)
Ранг ее также равен 3, следовательно, входное слово 0, 2 также является ДП для рассматриваемого БА. Таким образом, оба входных слова 3, 0 и 0, 2 являются для рассматриваемого БА одновременно УП и ДП.
Вопросы и упражнения
- Приведите определение билинейного автомата и выпишите уравнения состояний и выходов, описывающие его функционирование.
- Дайте определения синхронизирующей, установочной и диагностической последовательностей билинейного автомата в терминах его характеристических матриц.
- Сформулируйте и докажите критерий существования синхронизирующей последовательности для билинейного автомата.
- Опишите аналитический метод построения синхронизирующей последовательности для билинейного автомата.
- Сформулируйте и докажите критерий существования установочной последовательности для билинейного автомата.
- Опишите аналитический метод построения установочной последовательности для билинейного автомата.
- Сформулируйте и докажите критерий существования диагностической последовательности для билинейного автомата.
- Опишите аналитический метод построения диагностической последовательности для билинейного автомата.
