НОУ ИНТУИТ | Теория экспериментов с конечными автоматами. Лекция 18: Оптимальные эксперименты с линейными автоматами

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 17.02.2011 | Доступ: свободный | Студентов: 367 / 35 | Оценка: 5.00 / 5.00 | Длительность: 25:24:00

ISBN: 978-5-9963-0268-0

Тема: Алгоритмы и дискретные структуры

Специальности: Математик

|

Вам нравится? Нравится 3 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Синтез обобщенной синхронизирующей последовательности с минимальным числом перепадов

Ниже рассматривается задача, аналогичная задаче предыдущего раздела, где вместо минимизации весовой функции 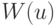W(u) будет осуществляться минимизацией иной функции.

Предварительно дадим краткое содержательное пояснение. Известно, что для цифровых устройств, реализованных с применением так называемой К-МОП- технологии, из двух равных по длине входных последовательностей более предпочтительной является та из них, у которой меньше число перепадов. Под перепадом сигналов в последовательности понимается наличие ситуации, когда два соседних символа в этой последовательности инверсны друг другу. К примеру, последовательность 00101011 имеет 5 перепадов.

Введем в рассмотрение следующую функцию:

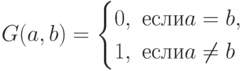
$G(a,b)= \begin {cases} 0,\ если a=b,\\ 1,\ если a \ne b \end {cases}$

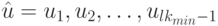Если и - два символа некоторой входной последовательности, то по значению G(a,b) можно судить о наличии или отсутствии перепада сигналов. Тогда задача построения ОСП $\hat u=u_1, u_2, \dots, u_{lk_{min}-1}$ с минимальным числом перепадов сигналов, переводящей обобщенно синхронизируемый автомат в заданное ОС $[\bar s]_{\mu}$ , формулируется следующим образом:

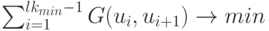$\sum_{i=1}^{lk_{min}-1}G(u_i, u_{i+1}) \to min$

( 18.11)

$Q \hat u=[\bar s]_{\mu}+p\bar d$

( 18.12)

$0 \le u_i \le p-1, 1 \le I \le lk_{min}$

( 18.13)

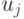Заметим, что количество переменных в этой задаче может быть уменьшено. Действительно, некоторые элементы матрицы могут быть нулевыми и потому в левой части системы (18.12) соответствующие переменные будут отсутствовать. Далее эти переменные будем именовать независимыми, а остальные переменные - зависимыми. Предположим, что в оптимальном плане $\hat u$ задачи (18.11)-(18.13) u_i и u_j есть значения зависимых координат, а координаты с номерами 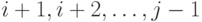$i+1, i+2, \dots, j-1$ являются независимыми. 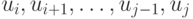Тогда если u_i=u_j , то на участке ( $u_i, u_{i+1}, \dots, u_{j-1}, u_j$ ) входной последовательности $\hat u$ перепады сигналов отсутствуют, а если $u_i \ne u_j$ , то имеется ровно один перепад. 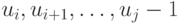Понятно, что если на упомянутом участке входной последовательности $\hat u$ исключить переменные $u_i, u_{i+1}, \dots, u_j-1}$ , то значение целевой функции (18.11) на укороченной таким образом входной последовательности не изменится. Поэтому целевую функцию (18.11) можно рассматривать на множестве векторов, составленных только из зависимых координат вектора $\hat u$ . Видоизмененную таким образом целевую функцию будем называть приведенной, так же будем называть и соответствующую задачу.

Ясно, что минимальное значение целевой функции в приведенной задаче равно ее минимальному значению в исходной задаче (18.11)-(18.13). Оптимальный план исходной задачи можно получить из оптимального плана приведенной задачи, если зависимые переменные положить равными соответствующим переменным из решения приведенной задачи, а значение каждой независимой переменной 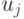u_j положить равным значению зависимой переменной u_i с максимальным номером , таким, что i<j . Если такой номер отсутствует, т. е. 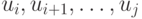все переменные $u_i, u_{i+1}, \dots, u_j$ являются независимыми, то положим их равными значению зависимой переменной 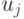u_j с таким минимальным номером , что i<j .

Из вида целевой функции (18.11) следует, что она не является линейной. Вместе с тем покажем, что исходная задача (18.11)-(18.13) может быть сведена к линейной задаче за счет введения дополнительных переменных.

Рассмотрим задачу

$\sum_{i=1}^{lk_{min}-1}g_i \to min$

( 18.14)

со следующими ограничениями:

$Q\hat u=[\bar s]_{\mu}+p \bar d$

( 18.15)

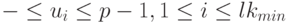$- \le u_i \le p-1, 1 \le i \le lk_{min}$

( 18.16)

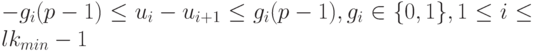$-g_i(p-1) \le u_i -u_{i+1} \le g_i(p-1), g_i \in \{0,1\}, 1 \le i \le lk_{min}-1$

( 18.17)

Введем следующее обозначение: 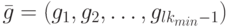$\bar g=(g_1, g_2, \dots, g_{lk_{min}-1})$ .

Теорема 18.4. Если 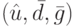$(\hat u, \bar d, \bar g)$ - оптимальный план задачи (18.14)-(18.17), то 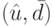$(\hat u, \bar d)$ является оптимальным планом задачи (18.11)-(18.13) и значения (18.14) и (18.11) на соответствующих оптимальных планах совпадают.

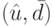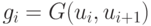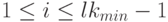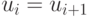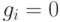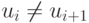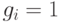Доказательство. Пусть $(\hat u, \bar d)$ есть оптимальный план задачи (18.11)-(18.13). Положим $g_i=G(u_i, u_{i+1})$ при $1 \le i \le lk_{min}-1$ , тогда для построенного таким образом множества величин g_i выполняются неравенства (18.17). В самом деле, если $u_i=u_{i+1}$ , то g_i=0 и неравенство (18.17) выполнено; если $u_i \ne u_{i+1}$ , то g_i=1 и неравенство (18.17) принимает вид

$-p+1 \le u_i - u_{i+1} \le p-1$

При ограничении (18.16) на значения u_i последнее неравенство также выполняется. Таким образом, поскольку ограничения на вектор $\hat u$ в задачах (18.11)-(18.13) и (18.14)-(18.17) совпадают, то для последней задачи $(\hat u, \bat d, \bar g)$ является допустимым планом, причем значения целевых функций соответствующих задач на двух приведенных планах совпадают.

Итак, всякому допустимому плану 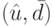$(\hat u, \bar d)$ задачи (18.11)-(18.13) соответствует допустимый план 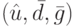$(\hat u, \bar d, \bar g)$ задачи (18.14)-(18.17) с одинаковыми значениями целевых функций, а на всяком оптимальном плане 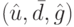$(\hat u, \bar d, \hat g)$ задачи (18.14)-(18.17) значение целевой функции (18.14) совпадает со значением целевой функции (18.11) на плане 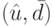$(\hat u, \bar d)$ задачи (18.11)-(18.13). Отсюда следует, что если 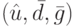$(\hat u, \bar d, \bar g)$ есть оптимальный план задачи (18.14)-(18.17), то 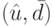$(\hat u, \bar d)$ является оптимальным планом задачи (18.11)-(18.13). В самом деле, в противном случае существует план 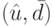$(\hat u, \bar d)$ , для которого 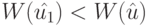$W(\hat {u_1}) < W(\hat u)$ , но тогда план 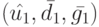$(\hat {u_1}, \bar {d_1}, \bar {g_1})$ лучше плана 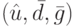$(\hat u, \bar d, \bar g)$ , что противоречит выбору.

Из теоремы 18.4 следует, что рассматриваемая нами задача (18.11)-(18.13) может быть сведена к линейной задаче и по найденному оптимальному плану последней легко построить оптимальный план исходной задачи.

Проиллюстрируем изложенное на примере ЛА, заданного над полем 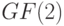GF(2) следующими характеристическими матрицами:

$A= \left [ \begin {matrix} 0&0&0&0\\ 1&0&0&0\\ 1&1&0&0\\ 1&1&1&0 \end {matrix} \right ], B= \left [ \begin {matrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end {matrix} \right ]$

Система уравнений перехода в координатной форме для этого ЛА имеет следующий вид:

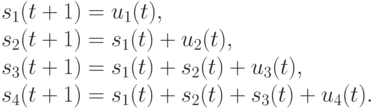
$s_1(t+1)=u_1(t),\\ s_2(t+1)=s_1(t)+u_2(t),\\ s_3(t+1)=s_1(t)+ s_2(t)+u_3(t),\\ s_4(t+1)=s_1(t)+s_2(t)+s_3(t)+u_4(t).$

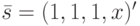Пусть $\mu =3$ и требуется установить этот ЛА в обобщенное состояние $\bar s=(1,1,1,x)'$ . Начнем с проверки того, является ли заданный ЛА обобщенно синхронизируемым. Вычислим с этой целью матрицы

$A^2= \left [ \begin {matrix} 0&0&0&0\\ 0&0&0&0\\ 1&0&0&0\\ 0&1&0&0\\ \end {matrix} \right ] A^3= \left [ \begin {matrix} 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 1&0&0&0 \end {matrix} \right ]$

Отсюда видно, что необходимое условие обобщенной синхронизируемости $[A]_{\mu}$ выполняется при k=3 и не выполняется при k<3 . Следовательно, минимальная ОСП для данного ЛА имеет длину 3.

Найдем матрицу линейных ограничений на допустимый план

$Q=[A^2B,AB,B]_3= \left [ \begin {matrix} 0&0&0&0&0&0&0&0&1&0&0&0\\ 0&0&0&0&1&0&0&0&0&1&0&0\\ 1&0&0&0&1&1&0&0&0&0&1&0 \end {matrix} \right ]$

Система сравнений $Q \hat u=[\bar s]_{\mu} mod 2$ , представляя собой линейные ограничения на переменные задачи, принимает вид

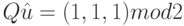
$Q\hat u=(1,1,1) mod 2$

где

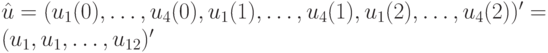
$\hat u=(u_1(0), \dots, u_4(0), u_1(1), \dots, u_4(1), u_1(2), \dots, u_4(2))'=(u_1, u_1, \dots, u_{12})'$

Перепишем эту систему в координатной форме:

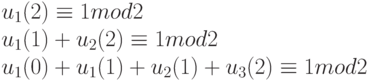
$u_1(2) \equiv 1 mod 2\\ u_1(1)+u_2(2) \equiv 1 mod 2\\ u_1(0)+u_1(1)+u_2(1)+u_3(2) \equiv 1 mod 2$

В соответствии с изложенным выше эквивалентная система линейных алгебраических уравнений (18.15) примет вид (с учетом перенумерации переменных от 1 до 12)

$u_9-2d_1=1,\\ u_5+u_{10}-2d_2=1,\\ u_1+u_5+u_6+u_{11}-2d_3=1,$

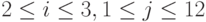где $u_j \in \{0,1\}, d_i$ - целые неотрицательные числа, $2 \le i \le 3, 1 \le j \le 12$ .

Из полученных уравнений вытекает, что 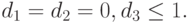$d_1=d_2=0, d_3 \le 1.$ Тогда исходная задача построения ОСП с минимальным числом перепадов сигналов для заданного ЛА эквивалентна задаче целочисленного линейного программирования:

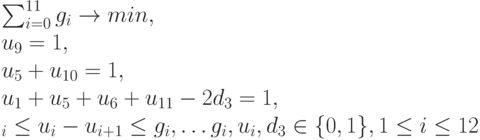
$\sum_{i=0}^{11}g_i \to min,\\ u_9=1,\\ u_5+u_{10}=1,\\ u_1+u_5+u_6+u_{11}-2d_3=1,\\ \g_i \le u_i-u_{i+1} \le g_i, \dots g_i, u_i, d_3 \in \{0,1\}, 1 \le i \le 12$

Заметим, что в данном случае линейность задачи не столь существенна, поскольку на этапе оценки решать непрерывные задачи большой размерности с помощью симплекс-метода не потребуется. Поэтому применим к исходной задаче метод, изложенный в предыдущем разделе. Эта задача выглядит так:

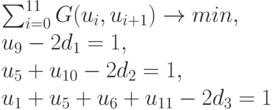
$\sum_{i=0}^{11} G(u_i, u_{i+1}) \to min,\\ u_9-2d_1=1,\\ u_5+u_{10}-2d_2=1,\\ u_1+u_5+u_6+u_{11}-2d_3=1$

где 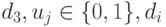$d_3, u_j \in \{0,1\}, d_i$ - целые неотрицательные числа, 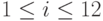$1 \le i \le 12$ . Формально эта задача имеет 13 переменных.

Способом, описанным выше, сократим количество переменных до 6, оставляя для рассмотрения лишь зависимые переменные

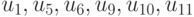
$u_1, u_5, u_6, u_9, u_{10}, u_{11}$

Таким образом, приведенная задача примет вид

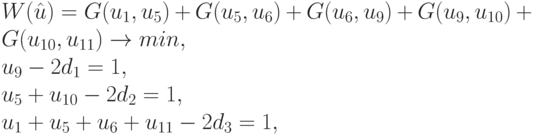
$W(\hat u)=G(u_1, u_5)+G(u_5, u_6)+G(u_6, u_9)+G(u_9, u_{10})+G(u_{10}, u_{11}) \to min,\\ u_9-2d_1=1,\\ u_5+u_{10}-2d_2=1,\\ u_1+u_5+u_6+u_{11}-2d_3=1,\\$

где

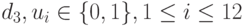
$d_3, u_i \in \{0,1\}, 1 \le i \le 12$

Из условия 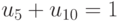$u_5+u_{10}=1$ следует, что 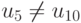$u_5 \ne u_{10}$ , поэтому среди пар 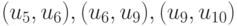$(u_5, u_6),(u_6, u_9),(u_9, u_{10})$ соседних координат вектора приведенной задачи имеется не менее одного перепада.

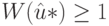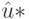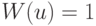Таким образом, получаем оценку $W(\hat u*) \ge 1$ для оптимального плана $\hat u*$ . Если существует план , для которого W(u)=1 , то он может быть выбран в качестве оптимального. Попытаемся найти такой план.

Разделим множество двоичных векторов задачи относительно переменной 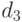d_3 . При d_3=1 получаем $u_1+u_5+u_6+u_{11}=3$ , из чего следует, что ровно одно из чисел равно 0, остальные равны 1.

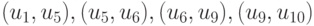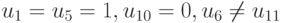Если $u_1 \ne u_5$ , то среди пар $(u_1, u_5), (u_5, u_6),(u_6, u_9), (u_9, u_{10})$ имеется не менее двух перепадов сигналов, поэтому рассмотрим случай u_1=u_5 . Тогда получаем $u_1=u_5=1, u_{10}=0, u_6 \ne u_{11}$ .

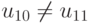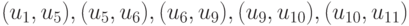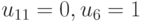Если $u_{10} \ne u_{11}$ , то снова получается по крайней мере два перепада сигналов среди пар $(u_1, u_5), (u_5, u_6),(u_6, u_9), (u_9, u_{10}), (u_{10}, u_{11})$ , в случае же $u_{10}=u_{11}$ получаем $u_{11}=0, u_6=1$ и среди пар соседних координат вектора (1,1,1,1,0,0) имеется один перепад сигналов. Это значение соответствует минимальной оценке функции , поэтому последний план является оптимальным планом приведенной задачи.

Для получения решения исходной задачи дополним полученный вектор значениями независимых координат так, как это было описано выше:

$\hat u*=(\mathdf 1,1,1,1, \mathdf 1, \mathdf 1,1,1, \mathdf 1,0,0,0)'$

Значения зависимых координат, по которым достраивался оптимальный план 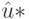$\hat u*$ , выделены жирным шрифтом.

Из полученного оптимального плана 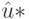$\hat u*$ сформируем теперь для заданного ЛА ОСП с минимальным числом перепадов сигналов:

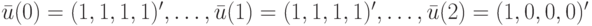
$\bar u(0)=(1,1,1,1)', \dots, \bar u(1)=(1,1,1,1)', \dots, \bar u(2)=(1,0,0,0)'$

Заметим в заключение, что специфика области применения предложенных методов в большинстве случаев позволяет понизить размерность задачи оптимизации путем сокращения количества ее переменных.

Что касается этапа оценки при решении задачи в используемом методе ветвей и границ, то в общем случае он сводится к решению соответствующих непрерывных задач.

Однако при p=2 их решение значительно упрощается, поскольку коэффициенты в ограничениях этих задач равны 0 или 1. Таким образом, специфика рассматриваемой задачи значительно сокращает трудность ее решения по сравнению со многими другими задачами, решаемыми с помощью метода ветвей и границ.

Вопросы и упражнения

Поясните понятие взвешенного алфавита и его содержательный смысл и понятие оптимального эксперимента.
Сформулируйте математическую постановку задачи построения синхронизирующей последовательности минимального веса, переводящей ЛА из любого состояния в заданное синхросостояние.
Опишите метод сведения задачи поиска обобщенной синхронизирующей последовательности минимального веса для ЛА к задаче целочисленного линейного программирования с линейными ограничениями.
Дайте содержательные пояснения понятию перепада сигналов во входной последовательности.
Опишите идею метода решения задачи построения обобщенной синхронизирующей последовательности для ЛА с минимальным числом перепадов.

Дальше >>

Авторизоваться

Теория экспериментов с конечными автоматами

Оптимальные эксперименты с линейными автоматами

Синтез обобщенной синхронизирующей последовательности с минимальным числом перепадов

Вопросы и упражнения

Вопросы и ответы