Эксперименты по распознаванию неисправностей линейных автоматов
Синтез тестов для нестационарных линейных автоматов
Для нестационарных ЛА рассмотрим ту же задачу, которая исследовалась в предыдущем разделе для стационарных ЛА. При этом будем предполагать, что класс неисправностей, возникающих в НЛА, полностью идентичен соответствующему классу в случае стационарных ЛА.
По аналогии со стационарными ЛА вначале рассмотрим метод синтеза тестов для синхронизируемых НЛА. Идея этого метода ничем не отличается от случая стационарного ЛА, и поэтому мы обозначим только некоторые его ключевые моменты.
Как и ранее, предполагается, что исправный и неисправный НЛА являются синхронизируемыми, однако длины минимальных СП для них не обязательно совпадают. Пусть 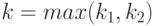 , где
, где 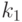 и
и  - длины минимальных СП для исправного НЛА
- длины минимальных СП для исправного НЛА  и неисправного НЛА
и неисправного НЛА 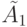 соответственно. Используя формулу (1.8) полной реакции НЛА и необходимое и достаточное условие (2.11) существования СП длины
соответственно. Используя формулу (1.8) полной реакции НЛА и необходимое и достаточное условие (2.11) существования СП длины  , как и в случае стационарного ЛА приходим к выводу, что поиск искомой тестовой последовательности
, как и в случае стационарного ЛА приходим к выводу, что поиск искомой тестовой последовательности 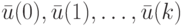 для обнаружения заданной неисправности сводится к решению системы линейных алгебраических уравнений следующего вида
для обнаружения заданной неисправности сводится к решению системы линейных алгебраических уравнений следующего вида
![\sum_{i-0}^{k-1}[C(k)A(k-1) \dots A(i+1)B(i)-C_1(k)A_1(k-1) \dots A_1(i+1)B_1(i)] \bar u(i)+\\
+[D(k)-D_1(k)] \bar u(k)=y](/sites/default/files/tex_cache/7ce729931569d8708e72af8b8257bc0d.png) |
( 14.18) |
Здесь y - некоторый ненулевой вектор, а матрица, снабженная индексом "1", относится к неисправному НЛА.
Множество всех искомых тестов может быть получено путем решения СЛАУ (14.8) для всевозможных ненулевых правых ее частей. Поскольку этот способ требует рассмотрения множества СЛАУ, более эффективным является другой способ, основанный на поиске решения одной однородной СЛАУ, соответствующей неоднородной системе (14.8), с последующим построением с помощью "однородного" решения искомых "неоднородных".
Вообще говоря, может оказаться, что при рассматриваемом значении  система (14.8) не является совместной ни при каких правых частях. В этом случае увеличим
система (14.8) не является совместной ни при каких правых частях. В этом случае увеличим  на единицу и будем строить новую систему вида (14.8). Этот процесс продолжается далее аналогичным образом до тех пор, пока либо не будет найдено множество всех тестов, либо величина
на единицу и будем строить новую систему вида (14.8). Этот процесс продолжается далее аналогичным образом до тех пор, пока либо не будет найдено множество всех тестов, либо величина  не достигнет верхней границы длины минимального теста. Такой границей, в частности, может служить верхняя оценка длины минимальной УП [67].
не достигнет верхней границы длины минимального теста. Такой границей, в частности, может служить верхняя оценка длины минимальной УП [67].
Проиллюстрируем предложенный метод на примере. Пусть 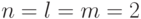 и НЛА над полем GF(2) задана следующими характеристическими матрицами:
и НЛА над полем GF(2) задана следующими характеристическими матрицами:
![A(0)=
\left [
\begin {matrix}
1&0\\
1&0
\end {matrix}
\right ],\\
A(1)=
\left [
\begin {matrix}
0&0\\
1&1
\end {matrix}
\right ], \\
A(2)=
\left [
\begin {matrix}
1&1\\
1&1
\end {matrix}
\right ],\\
A(i)=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ], i= 3,4, \dots ;\\
B(0)=
\left [
\begin {matrix}
0&0\\
0&0
\end {matrix}
\right ],\\
B(1)=
\left [
\begin {matrix}
1&1\\
0&0
\end {matrix}
\right ], \\
B(2)=
\left [
\begin {matrix}
0&1\\
1&0
\end {matrix}
\right ], \\
B(i)=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ], i=3,4, \dots ;\\
C(i)=D(i)=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ], i=3,4, \dots.](/sites/default/files/tex_cache/431752d4eba700a8017500846f9aaea1.png)
Предположим, что неисправный НЛА задается следующими характеристическими матрицами:
![A_1(0)=
\left [
\begin {matrix}
1&0\\
1&0
\end {matrix}
\right ],\\
A_1(1)=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ],
A_1(2)=
\left [
\begin {matrix}
0&0\\
1&1
\end {matrix}
\right ],\\
A_1(i)=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ], i= 3, 4, \dots ;\\
B_1(0)=
\left [
\begin {matrix}
0&\\
0&0
\end {matrix}
\right ],\\
B_1(1)=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ],\\
B_1(2)=
\left [
\begin {matrix}
0&1\\
1&0
\end {matrix}
\right ],\\
B_1(i)=
\left [
\begin {matrix}
1&0\\
0&0
\end {matrix}
\right ], i=3,4, \dots ;\\
C_1(i)=D_1(i)=
\left [
\begin {matrix}
1&0\\
0&1
\end {matrix}
\right ], i=3,4,\dots.](/sites/default/files/tex_cache/5c4c9dc19f32466ec374de0000e7fc3a.png)
Вычисления показывают, что ![A(1)A(0)=[0]](/sites/default/files/tex_cache/a9c38f42dc15c4572be18899e0c1caba.png) и
и ![A_1(2)A_1(1)A_1(0)=[0]](/sites/default/files/tex_cache/370ff398cf649aa47396e9923a3a3945.png) .
.
Следовательно, как исправный, так и неисправный НЛА синхронизируемы и длины СП для них равны 2 и 3 соответственно. Исходя из этого, начнем построение тестов длины 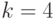 . Итак, вначале в качестве кандидата в тесты рассмотрим входную последовательность
. Итак, вначале в качестве кандидата в тесты рассмотрим входную последовательность 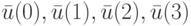 . Выпишем реакции на эту последовательность исправного и неисправного НЛА:
. Выпишем реакции на эту последовательность исправного и неисправного НЛА:
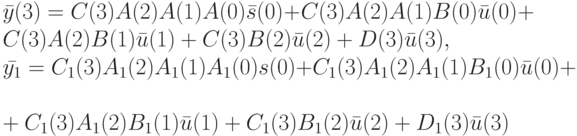
Выполнив соответствующие вычисления в координатной форме с учетом того, что все операции выполняются по модулю 2, получим следующие результаты:
![\bar y(3)=
\left [
\begin {matrix}
u_1(1)+u_2(1)+u_1(3)+u_2(2)\\
u_1(1)+u_2(1)+u_1(2)+u_2(3)
\end {matrix}
\right ],\\
y_1(3)=
\left [
\begin {matrix}
u_2(2)+u_1(3)\\
u_1(1)+u_2(1)+u_1(2)+u_2(3)
\end {matrix}
\right ]](/sites/default/files/tex_cache/eb4da3b28e9befc7420dcfdcaef4afd1.png)
Используя эти векторы, построим однородную систему, соответствующую системе (14.8):
![\bar y(3)+\bar {y_1}=
\left [
\begin {matrix}
u_1(1)+u_2(1)\\
0
\end {matrix}
\right ]=
\left [
\begin {matrix}
0\\
0
\end {matrix}
\right]](/sites/default/files/tex_cache/c9bd968cdc1793cbf3daae36dd20ff8a.png)
Ее решениями являются все четверки векторов 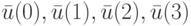 , у которых
, у которых  Отсюда следует, что искомое множество тестов составляет такие же четверки векторов, но для которых справедливо условие
Отсюда следует, что искомое множество тестов составляет такие же четверки векторов, но для которых справедливо условие  Легко подсчитать, что всего таких векторов 128 штук.
Легко подсчитать, что всего таких векторов 128 штук.
Предложенный метод предполагает сохранение свойства синхронизируемости у неисправного НЛА, если исправный НЛА был синхронизируем. Понятно, что это не всегда выполняется. В связи с этим рассмотрим метод синтеза тестов, ориентированный на произвольные минимальные НЛА. Этот метод есть прямой аналог метода распознавания автоматов, принадлежащих исключительному классу, описанному в [18].
Опишем кратко его суть применительно к рассматриваемой нами задаче, когда исключительный класс состоит только из двух автоматов, исправного и неисправного. При этом условимся считать, что множества их допустимых состояний совпадают с соответствующими множествами всех состояний автоматов.
Для исправного НЛА  построим минимальную УП
построим минимальную УП 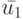 , которая существует в силу минимальности НЛА, и подадим ее на предъявленный для эксперимента экземпляр автомата. Естественно, что экспериментатору неизвестно, является ли этот автомат исправным или неисправным. По наблюдаемой реакции найдем конечное состояние
, которая существует в силу минимальности НЛА, и подадим ее на предъявленный для эксперимента экземпляр автомата. Естественно, что экспериментатору неизвестно, является ли этот автомат исправным или неисправным. По наблюдаемой реакции найдем конечное состояние  , в котором должен оказаться испытываемый автомат, если бы он был исправным.
, в котором должен оказаться испытываемый автомат, если бы он был исправным.
Далее построим УП  для неисправного НЛА
для неисправного НЛА 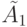 и подадим ее на предъявленный для эксперимента экземпляр автомата. По наблюдаемой реакции найдем конечное состояние
и подадим ее на предъявленный для эксперимента экземпляр автомата. По наблюдаемой реакции найдем конечное состояние  , в котором должен оказаться испытываемый автомат, если бы он был неисправным. Предполагается, что НЛА
, в котором должен оказаться испытываемый автомат, если бы он был неисправным. Предполагается, что НЛА 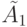 представлен своей минимальной формой и потому УП для него существует.
представлен своей минимальной формой и потому УП для него существует.
Напомним, что в силу теоремы 2.2 если НЛА имеет хотя бы одну УП длины  , то все другие входные последовательности длины
, то все другие входные последовательности длины  и более также являются для этого НЛА установочными. Это свойство позволяет "наложить" друг на друга УП
и более также являются для этого НЛА установочными. Это свойство позволяет "наложить" друг на друга УП 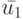 и
и 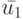 и тем самым сократить длину последовательности, осуществляющей установку НЛА
и тем самым сократить длину последовательности, осуществляющей установку НЛА  и
и 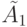 . В самом деле, если выбрать произвольную входную последовательность
. В самом деле, если выбрать произвольную входную последовательность 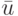 длины
длины 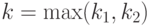 , где
, где 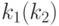 есть длина минимальной УП для автомата
есть длина минимальной УП для автомата 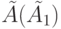 , то эта последовательность будет устанавливать в известное экспериментатору состояние как автомат
, то эта последовательность будет устанавливать в известное экспериментатору состояние как автомат  так и автомат
так и автомат 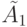 .
.
Для обнаружения неисправности теперь осталось ответить на вопрос, является ли испытываемый автомат автоматом  в состоянии
в состоянии  либо автоматом
либо автоматом 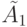 в состоянии
в состоянии 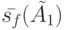 . Для ответа на этот вопрос подадим на вход испытываемого автомата входную последовательность, построенную на основе метода различающей функции. Синтез этой последовательности осуществим в виде пошагового процесса, делая попытки найти сначала последовательности длины 1, затем длины 2 и т. д. С этой целью сначала выпишем реакции автоматов
. Для ответа на этот вопрос подадим на вход испытываемого автомата входную последовательность, построенную на основе метода различающей функции. Синтез этой последовательности осуществим в виде пошагового процесса, делая попытки найти сначала последовательности длины 1, затем длины 2 и т. д. С этой целью сначала выпишем реакции автоматов  и
и 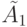 с начальными состояниями
с начальными состояниями  и
и 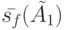 на входную последовательность
на входную последовательность  длины 1:
длины 1:
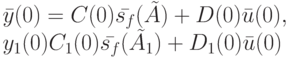
Теперь сформируем выражение (различающую функцию):
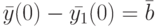
где  - некоторый произвольный ненулевой вектор. Это выражение будем интерпретировать как СЛАУ относительно координат
- некоторый произвольный ненулевой вектор. Это выражение будем интерпретировать как СЛАУ относительно координат  . Решая эту систему при всевозможных ненулевых правых частях, найдем все различающие последовательности длины 1. Если эта система окажется несовместной, сформируем очередную систему
. Решая эту систему при всевозможных ненулевых правых частях, найдем все различающие последовательности длины 1. Если эта система окажется несовместной, сформируем очередную систему

и ищем ее решение. Указанный процесс продолжается далее аналогичным образом до тех пор, пока не будет найдена различающая последовательность. Этот процесс заведомо конечен, поскольку неисправности в НЛА предполагаются существенными, т. е. проявляющими себя в процессе функционирования. Кстати, вывод о конечности процесса построения различающей последовательности следует также и из того факта, что упомянутая последовательность есть не что иное, как ДП минимального автомата для двух допустимых начальных состояний. Такая диагностическая задача, как известно [18], всегда разрешима.
Таким образом, искомый тест будет состоять из двух последовательностей, первая из которых представляет собой совмещенную УП, а вторая - различающую последовательность.
Остановимся теперь на верхней оценке длины теста, полученного описанным методом.
В разделе 2.3 лекции 2 было показано, что в общем случае длина минимальной УП для НЛА не ограничена сверху. Поэтому рассмотрим периодические НЛА, у которых длина УП, а следовательно, и теста, заведомо конечна.
В том же разделе 2.3 было установлено, что для периодического НЛА длина УП не превосходит 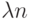 где
где  - период главной характеристической матрицы
- период главной характеристической матрицы  НЛА
НЛА  ,
,  - ее размерность. Что касается второй части теста, то ее можно рассматривать как ДП и поэтому длина ее не превосходит
- ее размерность. Что касается второй части теста, то ее можно рассматривать как ДП и поэтому длина ее не превосходит  . Таким образом, общая длина теста, построенного таким методом, не превышает величины
. Таким образом, общая длина теста, построенного таким методом, не превышает величины  .
.
Сравним эту оценку с соответствующей верхней оценкой длины теста для произвольного автомата, не являющегося НЛА. Как показано в [18] , верхняя оценка длины теста в этом случае такова:
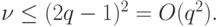
Здесь  - число состояний автомата. Поскольку для НЛА
- число состояний автомата. Поскольку для НЛА 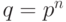 , в терминах параметра
, в терминах параметра  оценка длины теста для НЛА не превышает
оценка длины теста для НЛА не превышает 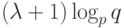 , что значительно ниже
, что значительно ниже 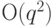 .
.
Вопросы и упражнения
- Дайте определение теста, обнаруживающего заданную неисправность в ЛА.
- Сформулируйте определение конечной памяти глубины
 линейного автомата и µ-определенного автомата.
линейного автомата и µ-определенного автомата. - Приведите постановку задачи построения теста, обнаруживающего заданную неисправность.
- К какой математической задаче сводится задача построения теста?
- Опишите метод построения теста для
 -определенного и синхронизируемого линейного автомата.
-определенного и синхронизируемого линейного автомата. - Опишите метод построения теста для произвольных стационарных линейных автоматов.
- Чем от предыдущего метода отличается метод построения теста для нестационарных линейных автоматов?
- Как длина минимального теста для ЛА связана с глубиной его памяти?
- Для примера ЛА из раздела 2.1 лекции 2 постройте тест для обнаружения неисправности, отличающейся от заданной в разделе 2.1 тем, что вторая (единичная) строка в главной матрице неисправного ЛА заменена нулевой строкой.
