Синхронизация и устойчивость дискретных линейных систем
Введем теперь некоторую модификацию понятия СП.
Определение 13.5. Бесконечную последовательность 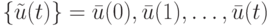 назовем
назовем 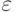 -синхронизирующей (
-синхронизирующей (  -СП) для ДЛС над полем
-СП) для ДЛС над полем  с множеством допустимых начальных состояний
с множеством допустимых начальных состояний  , если
, если

где 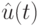 - начальный отрезок длины
- начальный отрезок длины  входной последовательности
входной последовательности  .
.
Поясним содержательно различие между СП и 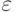 -СП. После подачи СП (она имеет конечную длину) ДЛС оказывается в одном и том же известном конечном состоянии. В то же время после подачи начального отрезка
-СП. После подачи СП (она имеет конечную длину) ДЛС оказывается в одном и том же известном конечном состоянии. В то же время после подачи начального отрезка 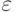 -СП ДЛС переводится хотя и в различные конечные состояния, но расстояние между ними может быть сделано меньше любого заранее заданного числа
-СП ДЛС переводится хотя и в различные конечные состояния, но расстояние между ними может быть сделано меньше любого заранее заданного числа  за счет подходящего выбора длины упомянутого начального отрезка.
за счет подходящего выбора длины упомянутого начального отрезка.
Теорема 13.5. Для того чтобы ДЛС 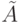 , у которой множество допустимых начальных состояний
, у которой множество допустимых начальных состояний  ограничено, имела
ограничено, имела 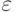 -СП, достаточно, чтобы все собственные числа
-СП, достаточно, чтобы все собственные числа 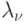 ее характеристической матрицы
ее характеристической матрицы  лежали внутри единичного круга
лежали внутри единичного круга
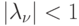 |
( 13.5) |
Доказательство. Проведем его для случая, когда все собственные числа матрицы A различны. Как следует из определения 13.5, существование  -СП
-СП  эквивалентно тому, что
эквивалентно тому, что
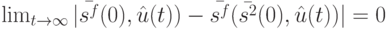
В силу аналога формулы (1.3) для ДЛС этот предел эквивалентен

По условию теоремы  и
и 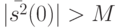 , где
, где 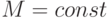 , но тогда и для состояния
, но тогда и для состояния 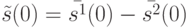 выполняется неравенство
выполняется неравенство  .
.
Рассмотрим ДЛС 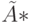 , заданную уравнением переходов
, заданную уравнением переходов
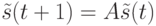 |
( 13.6) |
Очевидно, что существование  -СП для ДЛС
-СП для ДЛС 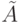 эквивалентно выполнению следующего равенства для ДЛС
эквивалентно выполнению следующего равенства для ДЛС 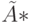 :
:
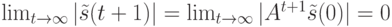
Введем замену  , где
, где 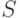 - невырожденная матрица, столбцами которой являются собственные векторы матрицы
- невырожденная матрица, столбцами которой являются собственные векторы матрицы  , причем
, причем
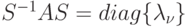
где 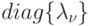 - диагональная матрица. Если
- диагональная матрица. Если  , то, очевидно, и
, то, очевидно, и 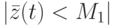 , где
, где 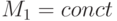 . Из уравнения (13.6) следует, что
. Из уравнения (13.6) следует, что
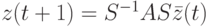
или в координатной форме  .
.
Учитывая, что
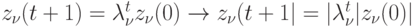
в силу условия (13.5) и того факта, что 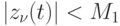 , получаем
, получаем
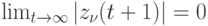
Отсюда вытекает, что
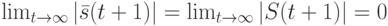
а это, как было упомянуто выше, эквивалентно существованию  -СП для ДЛС
-СП для ДЛС 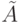 .
.
Заметим, что эта теорема остается справедливой и в случае кратных собственных чисел, но доказательство ее немного усложняется.
Следствие. Если у ДЛС 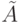 над полем
над полем  все собственные числа характеристической матрицы
все собственные числа характеристической матрицы  лежат внутри единичного круга, то любая бесконечная входная последовательность
лежат внутри единичного круга, то любая бесконечная входная последовательность  является для нее
является для нее  -СП.
-СП.
Справедливость следствия вытекает из того, что в условиях теоремы 13.5 входная последовательность  является произвольной.
является произвольной.
Коснемся теперь связи между устойчивостью ДЛС над полем  и свойством
и свойством  -синхронизации. Напомним [38], что свободная ДЛС над полем
-синхронизации. Напомним [38], что свободная ДЛС над полем  называется устойчивой по начальным условиям, если
называется устойчивой по начальным условиям, если
![\lim_{t \to \infty}\bar s(t)=[0]](/sites/default/files/tex_cache/ba5250fec327d34581d2db5a56f2ae78.png)
ДЛС, для которой из условия 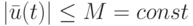 следует ограниченность
следует ограниченность 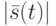 , называется устойчивой к внешним возмущениям. При наличии обоих указанных свойств ДЛС называется устойчивой.
, называется устойчивой к внешним возмущениям. При наличии обоих указанных свойств ДЛС называется устойчивой.
Понятно, что из устойчивости ДЛС по начальным условиям вытекает справедливость равенства

Последнее означает, что бесконечная нулевая входная последовательность является для ДЛС  -СП.
-СП.
Известно [38], что условие (13.5) есть достаточное условие устойчивости. Таким образом, из теоремы 13.5 следует, что для свободной ДЛС в случае выполнения условия (13.5) понятие  -синхронизации и устойчивости равносильны.
-синхронизации и устойчивости равносильны.
Из существования СП следует существование  -СП (она состоит из двух подпоследовательностей, первая из которых совпадает с СП, а вторая, бесконечная, может выбираться произвольно), однако обратная импликация места не имеет.
-СП (она состоит из двух подпоследовательностей, первая из которых совпадает с СП, а вторая, бесконечная, может выбираться произвольно), однако обратная импликация места не имеет.
Состояние ДЛС 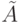 , в которое она переходит после подачи на ее входы СП (
, в которое она переходит после подачи на ее входы СП (  -СП), назовем синхросостоянием. Ясно, что в общем случае различные СП (
-СП), назовем синхросостоянием. Ясно, что в общем случае различные СП (  -СП) могут переводить ДЛС как в различные, так и совпадающие синхросостояния.
-СП) могут переводить ДЛС как в различные, так и совпадающие синхросостояния.
В разделе 1.2 лекции 1 была рассмотрена задача о переводе ЛА над полем 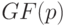 в заданное синхросостояние с помощью СП. Точно такая же задача может быть сформулирована и для ДЛС над полем
в заданное синхросостояние с помощью СП. Точно такая же задача может быть сформулирована и для ДЛС над полем  , и метод ее решения аналогичен методу, предложенному для случая ЛА.
, и метод ее решения аналогичен методу, предложенному для случая ЛА.
Сформулируем подобную задачу для ДЛС, когда в качестве "переводящей" последовательности используется  -СП.
-СП.
Пусть заданы ДЛС 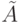 размерности
размерности  над полем
над полем  , синхросостояние
, синхросостояние 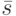 и величина
и величина  . Требуется найти входную последовательность конечной длины (начальный отрезок
. Требуется найти входную последовательность конечной длины (начальный отрезок  -СП), которая переводит ДЛС в такое состояние
-СП), которая переводит ДЛС в такое состояние 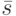 , что
, что  .
.
Пусть множество 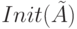 допустимых начальных состояний ДЛС
допустимых начальных состояний ДЛС 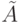 ограничено и для любого
ограничено и для любого
![\tilde s=[s_1*, \dots, s_n*] \in Init(\tilde A)](/sites/default/files/tex_cache/022db06a1a63914f8f60ce391265502b.png)
 |
( 13.7) |
Очевидно, что если
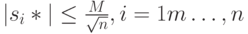
то неравенство (13.7) заведомо будет выполнено. Теперь найдем такое минимальное число  , чтобы выполнялось неравенство
, чтобы выполнялось неравенство

где ![\tilde s*=\left [ \frac {M}{\sqrt n}, \dots, \frac {M}{\sqrt n}\right ]](/sites/default/files/tex_cache/b6a8f8def37bac4ec669f1e3c8d636d7.png) .
.
Используя аналог формулы (1.3) для ДЛС 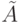 , выпишем следующее равенство:
, выпишем следующее равенство:
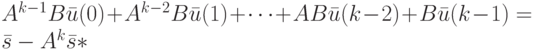 |
( 13.8) |
Его можно рассматривать как СЛАУ относительно координат векторов входной последовательности  . Понятно, что решение этой системы будет давать искомую входную последовательность.
. Понятно, что решение этой системы будет давать искомую входную последовательность.
Проиллюстрируем изложенное на примере. Пусть ДЛС над полем  с одним входным каналом задана характеристическими матрицами
с одним входным каналом задана характеристическими матрицами
![A=
\left [
\begin {matrix}
0.01&0.05&0.00\\
0.05&0.001&0.02\\
0.00&0.02&0.0001
\end {matrix}
\right ],
B=
\left [
\begin {matrix}
2.0\\
3.0\\
4.0
\end {matrix}
\right ]](/sites/default/files/tex_cache/24fe5bd479f6d02ec2cf9ad3ae326434.png)
Путем вычислений можно убедиться, что собственными значениями матрицы  являются числа
являются числа 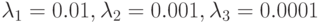 . Отсюда на основании теоремы 13.5 можно утверждать, что рассматриваемая ДЛС является синхронизируемой.
. Отсюда на основании теоремы 13.5 можно утверждать, что рассматриваемая ДЛС является синхронизируемой.
Пусть требуется перевести эту ДЛС в синхросостояние ![\bar s=[0.4,1.2,-0.3]'](/sites/default/files/tex_cache/acd650379ff7d97d7705a81056a93797.png) , и пусть точность, с которой это надо осуществить, равна
, и пусть точность, с которой это надо осуществить, равна  . Предположим, что для любого
. Предположим, что для любого  выполняется неравенство
выполняется неравенство  Отсюда получаем, что
Отсюда получаем, что ![\tilde s*=[0.75,0.75,0.75]'](/sites/default/files/tex_cache/703dfae9d8ac82de442b30042604a96d.png) .
.
Определим теперь минимальную начальную длину отрезка  -СП, обеспечивающую перевод рассматриваемой ДЛС в заданное синхросостояние с точностью
-СП, обеспечивающую перевод рассматриваемой ДЛС в заданное синхросостояние с точностью 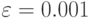 . В соответствии с изложенным вычислим
. В соответствии с изложенным вычислим
![A^2=
\left [
\begin {matrix}
0.0026&0.00055&0.001\\
0.00055&0.002901&0.000022\\
0.001&0.000022&0.0004
\end {matrix}
\right ],
A^2\tilde s*=
\left [
\begin {matrix}
0.00312\\
0.006312\\
0.001066
\end {matrix}
\right ],
|A^2\bar s*|=0.007141](/sites/default/files/tex_cache/6d4d99a2a5a0386893efe75b3e1d66da.png)
Поскольку  , вычислим
, вычислим
![A_3=
\left [
\begin {matrix}
0.0054&0.000151&0.000011\\
0.0002&0.000031&0.00\\
0.00011&0.000058&0.00
\end {matrix}
\right ],
A^3\tilde s*=
\left [
\begin {matrix}
0.00016\\
0.000173\\
0.000052
\end {matrix}
\right ],
|A^3\tilde s*|=0.000242](/sites/default/files/tex_cache/da75d7a373f5213b312f4b932378e956.png)
Поскольку 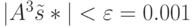 , заданная точность достигнута. Таким образом, начальный отрезок искомой
, заданная точность достигнута. Таким образом, начальный отрезок искомой  -СП, обеспечивающий перевод рассматриваемой ДЛС в синхросостояние
-СП, обеспечивающий перевод рассматриваемой ДЛС в синхросостояние ![[0.4,1.2-0.3]'](/sites/default/files/tex_cache/291fd54bdf41a2238c54141a807a56ce.png) с заданной точностью
с заданной точностью  , будет иметь длину
, будет иметь длину  . Исходя из этого, система (13.8) примет вид
. Исходя из этого, система (13.8) примет вид
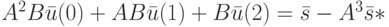
В координатной форме эта система такова:

Решая эту систему, получим следующий результат:

Итак, полученная входная последовательность переводит рассматриваемую ДЛС из любого состояния множества  , состоящего из всевозможных трехмерных векторов, длины которых не превосходят величины
, состоящего из всевозможных трехмерных векторов, длины которых не превосходят величины  , в состояния, отстоящие от заданного синхросостояния
, в состояния, отстоящие от заданного синхросостояния ![\bar s=[0.4,1.2,-0.3]'](/sites/default/files/tex_cache/acd650379ff7d97d7705a81056a93797.png) не более чем на 0.001.
не более чем на 0.001.
Сделаем замечание, касающееся методов решения системы уравнений вида (13.8). Отметим, что правая часть этой системы является не точной, а приближенной величиной. Это же относится и к элементам различных степеней матриц и произведений матриц, поскольку при их вычислении производятся округления. Поэтому для решения системы (13.8) целесообразно пользоваться приближенными методами. Сейчас известен широкий спектр подобных методов [4], каждый из которых характеризуется различными условиями сходимости, и поэтому для каждой конкретной системы вида (13.8) необходимо подбирать такой, который гарантирует сходимость. Что касается практической реализации, то приближенные методы к тому же, как правило, менее трудоемки, чем точные.
Приведенные выше результаты относились к стационарным ЛА. Что касается нестационарных ЛА, то полные аналоги этих результатов оказываются справедливыми и для них.
Так, определив для НЛА состояние равновесия и асимптотически устойчивое состояние равновесия, как это делалось для стационарных ЛА (определения 13.2 и 13.3 соответственно), легко доказать, что теоремы 13.1 и 13.2 остаются справедливыми и для НЛА. Формулировка теоремы 13.3 для НЛА претерпевает незначительное изменение.
Теорема 13.3. Для того чтобы свободный НЛА 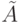 над полем
над полем 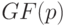 имел асимптотически устойчивое состояние равновесия, необходимо и достаточно, чтобы существовало такое целое положительное
имел асимптотически устойчивое состояние равновесия, необходимо и достаточно, чтобы существовало такое целое положительное  , что
, что
![A(t) A(t-1)\dots A(0) = [0]](/sites/default/files/tex_cache/9ab0a19d75ee41b9a1783341b97b2844.png)
Заметим, что для НЛА над полем 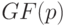 асимптотическая устойчивость и устойчивость в большом просто совпадают, как это было и для стационарных ЛА.
асимптотическая устойчивость и устойчивость в большом просто совпадают, как это было и для стационарных ЛА.
По аналогии с определением 13.5 для стационарных ЛА можно ввести понятие  -СП для нестационарного ЛА.
-СП для нестационарного ЛА.
Среди всего множества НЛА рассмотрим далее такой класс НЛА, у которых характеристические матрицы 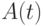 являются периодическими (с периодом
являются периодическими (с периодом 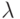 ), т. е. для них выполняется равенство
), т. е. для них выполняется равенство 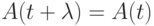 , где
, где 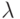 - целое положительное число. Построим стационарный ЛА
- целое положительное число. Построим стационарный ЛА 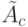 , согласованный с НЛА
, согласованный с НЛА 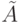 , задав функцию переходов ЛА
, задав функцию переходов ЛА 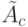 следующим образом:
следующим образом:
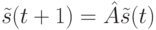
где 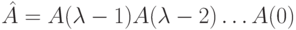 . Напомним [68], что спектральным радиусом
. Напомним [68], что спектральным радиусом 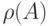 матрицы
матрицы  называют число
называют число 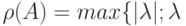 - собственные значения матрицы
- собственные значения матрицы 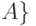 .
.
Теорема 13.6. Для того чтобы периодический НЛА 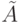 с ограниченным множеством
с ограниченным множеством 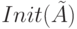 допустимых начальных состояний имел
допустимых начальных состояний имел  -СП, достаточно, чтобы при любом
-СП, достаточно, чтобы при любом  выполнялось неравенство
выполнялось неравенство
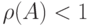 |
( 13.9) |
Доказательство. Как следует из определения  -СП, ее существование равносильно выполнению неравенства
-СП, ее существование равносильно выполнению неравенства
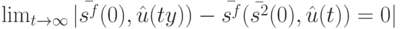 |
( 13.10) |
Здесь использованы те же обозначения, что и в определении 13.5. Если матрица 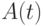 периодическая, то по индукции можно показать, что формула (1.7) примет вид
периодическая, то по индукции можно показать, что формула (1.7) примет вид
![\bar s(t+1)=A(t-\mu [t\ \mu])A(t-\mu [t\ \mu]-1) \dots A(0)\hat A\bar s(0)+A(t-\mu [t\ \mu])\dots\\
\dots A(1) \hat A^{[t\ \mu]}B(0)\bar u(0)+\dots +A(t)B(t-1)\bar u(t-1)+B(t)\bar u(t),](/sites/default/files/tex_cache/09e2a505d69661476fe9e5a77e0806d4.png) |
( 13.11) |
где ![[t\ \mu]](/sites/default/files/tex_cache/4ca9be841e45b4292aa558e6ee003c00.png) - целая часть числа
- целая часть числа 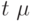 .
.
Из (13.11) следует, что (13.10) эквивалентно соответственно
![\lim_{t \to \infty}|A(t-\mu [t\ \mu])\dots A(0)\hat A^{[t\ \mu]}(\bar {s^1}(0)-\bar {s^2}(0)|=0](/sites/default/files/tex_cache/51d01e801257de925ece7bdbd2ed9c0a.png) |
( 13.12) |
Согласно лемме 5.6.10 из [68], существует по крайней мере одна матричная форма, для которой справедливы оценки  при заданном
при заданном  . Отсюда следует, что
. Отсюда следует, что
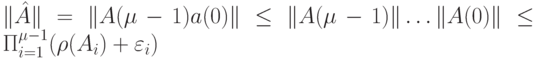
Поскольку по условиям теоремы  для
для 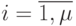 , при соответствующем выборе величин
, при соответствующем выборе величин 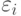 каждый из сомножителей в правой части последнего неравенства, а следовательно, и вся его правая часть, может быть сделана меньше единицы. Из этого следует (см. лемму 5.6.11 из [68]), что
каждый из сомножителей в правой части последнего неравенства, а следовательно, и вся его правая часть, может быть сделана меньше единицы. Из этого следует (см. лемму 5.6.11 из [68]), что
![\lim_{t \to \infty}\hat A^k=[0]](/sites/default/files/tex_cache/2f3591ab49ee470172fd12e9f4521215.png)
т. е. все элементы матрицы  стремятся к нулю при
стремятся к нулю при  .
.
Условимся говорить, что матрица  не превосходит матрицу
не превосходит матрицу  (
(  и
и  имеют одинаковую размерность), и писать
имеют одинаковую размерность), и писать  , если каждый элемент матрицы
, если каждый элемент матрицы  не превосходит соответствующего элемента матрицы
не превосходит соответствующего элемента матрицы  . Положим
. Положим

где  - элементы матрицы
- элементы матрицы  . Тогда при любом
. Тогда при любом 
![A(t -\mu [t\ \mu ]) \dots A(0)\hat A^{[t\ \mu]}(\bar {s^1}(0)-\bar {s^2}(0)) \le D(M) \hat A^{[t\ \mu]}(\bar {s^1}(0)-\bar {s^2}(0))](/sites/default/files/tex_cache/800e91f6e4256eca3f6cdaeed9f947ce.png) |
( 13.14) |
На основании (13.13) и (13.14) и того факта, что длина вектора  ограничена в силу ограниченности
ограничена в силу ограниченности  и
и 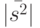 согласно условиям теоремы, вытекает справедливость (13.12).
согласно условиям теоремы, вытекает справедливость (13.12).
Следствие. Для периодического НЛА 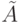 , у которого при любом
, у которого при любом  спектральный радиус матрицы
спектральный радиус матрицы 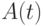 меньше 1, а множество
меньше 1, а множество 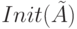 ограничено, любая бесконечная входная последовательность
ограничено, любая бесконечная входная последовательность  является
является  -синхронизирующей.
-синхронизирующей.
Можно показать, что по аналогии со стационарными ЛА для нестационарных ЛА при выполнении условий теоремы 13.6 понятие  -синхронизируемости и асимптотической устойчивости равнозначны.
-синхронизируемости и асимптотической устойчивости равнозначны.
Заметим, наконец, что решение задачи о переводе НЛА в заданное синхросостояние можно осуществить тем же самым методом, что описан для стационарного ЛА.
Вопросы и упражнения
- Дайте определения состояния равновесия и асимптотически устойчивого состояния свободного ЛА.
- Какова связь между синхронизируемостью ЛА и асимптотической устойчивостью состояний?
- Приведите постановку задачи стабилизации ЛА.
- Всегда ли разрешима эта задача для ЛА с парой ее невырожденных характеристических матриц?
- Дайте определение
 -синхронизирующей последовательности для дискретной линейной системы над полем R и поясните ее содержательный смысл.
-синхронизирующей последовательности для дискретной линейной системы над полем R и поясните ее содержательный смысл. - Сформулируйте достаточное условие существования
 -синхронизирующей последовательности для дискретной линейной системы над полем R.
-синхронизирующей последовательности для дискретной линейной системы над полем R. - Дайте определение синхросостояния дискретной линейной системы.
- Опишите метод решения задачи поиска входной последовательности, переводящей ДЛС из любого состояния в
 -окрестность состояний и выходов ЛА.
-окрестность состояний и выходов ЛА.
