|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистика интервальных данных
12.3. Интервальные данные в задачах проверки гипотез
С позиций статистики интервальных данных целесообразно изучить все практически используемые процедуры прикладной математической статистики, установить соответствующие нотны и рациональные объемы выборок. Это позволит устранить разрыв между математическими схемами прикладной статистики и реальностью влияния погрешностей наблюдений на свойства статистических процедур. Статистика интервальных данных - часть теории устойчивых статистических процедур, развитой в монографии [ [ 1.15 ] ]. Часть, более адекватная реальной статистической практике, чем некоторые другие постановки, например, с засорением нормального распределения большими выбросами.
Рассмотрим подходы статистики интервальных данных в задачах проверки статистических гипотез. Пусть принятие решения основано на сравнении рассчитанного по выборке значения статистики критерия  с граничным значением
с граничным значением  : если
: если  , то гипотеза отвергается, если же
, то гипотеза отвергается, если же  , то принимается. С учетом погрешностей измерений выборочное значение статистики критерия может принимать любое значение в интервале
, то принимается. С учетом погрешностей измерений выборочное значение статистики критерия может принимать любое значение в интервале ![[f(y)-N_f(y);\;f(y)+N_f(y)]](/sites/default/files/tex_cache/0defc514bac2e7ff86175c3ca7c16a84.png) . Это означает, что "истинное" значение порога, соответствующее реально используемому критерию, находится между
. Это означает, что "истинное" значение порога, соответствующее реально используемому критерию, находится между 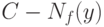 и
и 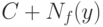 , а потому уровень значимости описанного правила (критерия) лежит между
, а потому уровень значимости описанного правила (критерия) лежит между 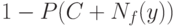 и
и 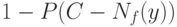 , где
, где 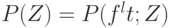 .
.
Пример 1. Пусть  - выборка из нормального распределения с математическим ожиданием
- выборка из нормального распределения с математическим ожиданием  и единичной дисперсией. Необходимо проверить гипотезу
и единичной дисперсией. Необходимо проверить гипотезу  при альтернативе
при альтернативе 
Как известно из любого учебного курса математической статистики, следует использовать статистику  и порог C=\Phi(1-\alpha/2), где
и порог C=\Phi(1-\alpha/2), где  - уровень значимости,
- уровень значимости,  - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. В частности,
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. В частности,  при
при  .
.
При ограничениях (1) на абсолютную погрешность 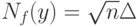 . Например, если
. Например, если 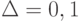 , а
, а 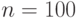 , то
, то 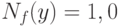 . Это означает, что истинное значение порога лежит между 0,96 и 2,96, а истинный уровень значимости - между 0,003 и 0,34. Можно сделать и другой вывод: нулевую гипотезу
. Это означает, что истинное значение порога лежит между 0,96 и 2,96, а истинный уровень значимости - между 0,003 и 0,34. Можно сделать и другой вывод: нулевую гипотезу  допустимо отклонить на уровне значимости 0,05 лишь тогда, когда
допустимо отклонить на уровне значимости 0,05 лишь тогда, когда  .
.
Если же 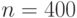 при
при 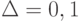 , то
, то 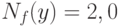 и
и  , в то время как
, в то время как 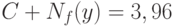 . Таким образом, даже в случае
. Таким образом, даже в случае 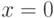 гипотеза
гипотеза  может быть отвергнута только из-за погрешностей измерений результатов наблюдений.
может быть отвергнута только из-за погрешностей измерений результатов наблюдений.
Вернемся к общему случаю проверки гипотез. С учетом погрешностей измерений граничное значение 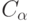 в статистике интервальных данных целесообразно заменить на
в статистике интервальных данных целесообразно заменить на 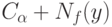 . Такая замена дает гарантию, что вероятность отклонения нулевой гипотезы
. Такая замена дает гарантию, что вероятность отклонения нулевой гипотезы  , когда она верна, не более
, когда она верна, не более  . При проверке гипотез аналогом статистической погрешности, рассмотренной выше в задачах оценивания, является
. При проверке гипотез аналогом статистической погрешности, рассмотренной выше в задачах оценивания, является 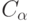 . Суммарная погрешность имеет вид
. Суммарная погрешность имеет вид 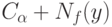 . Исходя из принципа уравнивания погрешностей [
[
1.15
]
], целесообразно определять рациональный объем выборки из условия
. Исходя из принципа уравнивания погрешностей [
[
1.15
]
], целесообразно определять рациональный объем выборки из условия

Если  , где
, где 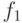 при справедливости
при справедливости  имеет асимптотически нормальное распределение с математическим ожиданием 0 и дисперсией
имеет асимптотически нормальное распределение с математическим ожиданием 0 и дисперсией  то
то
 |
( 47) |
 , где
, где  - квантиль порядка
- квантиль порядка  стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Из (47) вытекает, что в рассматриваемом случае
стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Из (47) вытекает, что в рассматриваемом случае
Пример 2. Рассмотрим статистику одновыборочного критерия Стьюдента
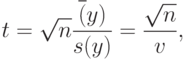
 - выборочный коэффициент вариации. Тогда с точностью до бесконечно малых более высокого порядка нотна для
- выборочный коэффициент вариации. Тогда с точностью до бесконечно малых более высокого порядка нотна для  имеет вид
имеет вид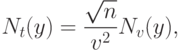
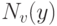 - рассмотренная ранее нотна для выборочного коэффициента вариации. Поскольку распределение статистики Стьюдента
- рассмотренная ранее нотна для выборочного коэффициента вариации. Поскольку распределение статистики Стьюдента  сходится к стандартному нормальному, то небольшое изменение предыдущих рассуждений дает
сходится к стандартному нормальному, то небольшое изменение предыдущих рассуждений дает
Пример 3. Рассмотрим двухвыборочный критерий Смирнова, предназначенный для проверки однородности (совпадения) функций распределения двух независимых выборок [ [ 12.44 ] ]. Статистика этого критерия имеет вид
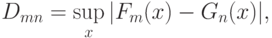
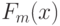 - эмпирическая функция распределения, построенная по первой выборке объема
- эмпирическая функция распределения, построенная по первой выборке объема  , извлеченной из генеральной совокупности с функцией распределения
, извлеченной из генеральной совокупности с функцией распределения  , а
, а  - эмпирическая функция распределения, построенная по второй выборке объема
- эмпирическая функция распределения, построенная по второй выборке объема  , извлеченной из генеральной совокупности с функцией распределения
, извлеченной из генеральной совокупности с функцией распределения 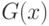 . Нулевая гипотеза имеет вид
. Нулевая гипотеза имеет вид 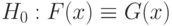 , альтернативная состоит в ее отрицании:
, альтернативная состоит в ее отрицании:  при некотором
при некотором  . Значение статистики сравнивают с порогом
. Значение статистики сравнивают с порогом 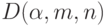 зависящим от уровня значимости
зависящим от уровня значимости  и объемов выборок
и объемов выборок  и
и  .
Если значение статистики не превосходит порога, то принимают нулевую гипотезу, если больше порога - альтернативную. Пороговые значения
.
Если значение статистики не превосходит порога, то принимают нулевую гипотезу, если больше порога - альтернативную. Пороговые значения 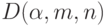 берут из таблиц [
[
2.1
]
]. Описанный критерий иногда неправильно называют критерием Колмогорова-Смирнова. История вопроса описана в [
[
12.34
]
].
берут из таблиц [
[
2.1
]
]. Описанный критерий иногда неправильно называют критерием Колмогорова-Смирнова. История вопроса описана в [
[
12.34
]
].При ограничениях (1) на абсолютные погрешности и справедливости нулевой гипотезы 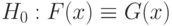 нотна имеет вид (при больших объемах выборок)
нотна имеет вид (при больших объемах выборок)

Если  при
при 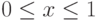 , то
, то  . С помощью условия
. С помощью условия  при уровне значимости
при уровне значимости  и достаточно больших объемах выборок (т.е. используя асимптотическое выражение для порога согласно [
[
2.1
]
]) получаем, что выборки имеет смысл увеличивать, если
и достаточно больших объемах выборок (т.е. используя асимптотическое выражение для порога согласно [
[
2.1
]
]) получаем, что выборки имеет смысл увеличивать, если

Правая часть этой формулы при 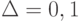 равна 46. Если
равна 46. Если  , то последнее неравенство переходит в
, то последнее неравенство переходит в  .
.
Теоретические результаты в области статистических методов входят в практику через алгоритмы расчетов, воплощенные в программные средства (пакеты программ, диалоговые системы). Ввод данных в современной статистической программной системе должен содержать запросы о погрешностях результатов измерений. На основе ответов на эти запросы вычисляются нотны рассматриваемых статистик, а затем - доверительные интервалы при оценивании, разброс уровней значимости при проверке гипотез, рациональные объемы выборок. Необходимо использовать систему алгоритмов и программ статистики интервальных данных, "параллельную" подобным системам для классической математической статистики.
