|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистика интервальных данных
Метрологические, методические, статистические и вычислительные погрешности. Целесообразно выделить ряд видов погрешностей статистических данных. Погрешности, вызванные неточностью измерения исходных данных, называем метрологическими. Их максимальное значение можно оценить с помощью нотны. Впрочем, выше на примере оценивания параметров гамма-распределения показано, что переход от максимального отклонения к реально имеющемуся в вероятностно-статистической модели не меняет выводы (с точностью до умножения предельных значений погрешностей  или
или 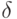 на константы). Как правило, метрологические погрешности не убывают с ростом объема выборки.
на константы). Как правило, метрологические погрешности не убывают с ростом объема выборки.
Методические погрешности вызваны неадекватностью вероятностно-статистической модели, отклонением реальности от ее предпосылок. Неадекватность обычно не исчезает при росте объема выборки. Методические погрешности целесообразно изучать с помощью "общей схемы устойчивости" [ [ 1.15 ] , [ 12.38 ] ], обобщающей популярную в теории робастных статистических процедур модель засорения большими выбросами. В настоящей главе методические погрешности не рассматриваются.
Статистическая погрешность - это та погрешность, которая традиционно рассматривается в математической статистике. Ее характеристики - дисперсия оценки, дополнение до 1 мощности критерия при фиксированной альтернативе и т.д. Как правило, статистическая погрешность стремится к 0 при росте объема выборки.
Вычислительная погрешность определяется алгоритмами расчета, в частности, правилами округления. На уровне чистой математики справедливо тождество правых частей формул (22) и (24), задающих выборочную дисперсию 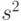 , а на уровне вычислительной математики формула (22) дает при определенных условиях существенно больше верных значащих цифр, чем вторая [
[
12.40
]
, с.51-52].
, а на уровне вычислительной математики формула (22) дает при определенных условиях существенно больше верных значащих цифр, чем вторая [
[
12.40
]
, с.51-52].
Выше на примере задачи оценивания параметров гамма-распределения рассмотрено совместное действие метрологических и вычислительных погрешностей, причем погрешности вычислений оценивались по классическим правилам для ручного счета [
[
12.4
]
]. Оказалось, что при таком подходе оценки метода моментов имеют преимущество перед оценками максимального правдоподобия в обширной области изменения параметров. Однако, если учитывать только метрологические погрешности, как это делалось выше в примерах 1-5, то с помощью аналогичных выкладок можно показать, что оценки этих двух типов имеют (при достаточно больших  ) одинаковую погрешность.
) одинаковую погрешность.
Вычислительную погрешность здесь подробно не рассматриваем. Ряд интересных результатов о ее роли в статистике получили Н.Н. Ляшенко и М.С. Никулин [ [ 12.20 ] ].
Проведем сравнение методов оценивания параметров в более общей постановке.
В теории оценивания параметров классической математической статистики установлено, что метод максимального правдоподобия, как правило, лучше (в смысле асимптотической дисперсии и асимптотического среднего квадрата ошибки), чем метод моментов. Однако в интервальной статистике это, вообще говоря, не так, что продемонстрировано выше на примере оценивания параметров гамма-распределения. Сравним эти два метода оценивания в случае интервальных данных в общей постановке. Поскольку метод максимального правдоподобия - частный случай метода минимального контраста, начнем с разбора этого несколько более общего метода.
Оценки минимального контраста. Пусть  - пространство, в котором лежат независимые одинаково распределенные случайные элементы
- пространство, в котором лежат независимые одинаково распределенные случайные элементы  .. Будем оценивать элемент пространства параметров
.. Будем оценивать элемент пространства параметров  с помощью функции контраста
с помощью функции контраста  . Оценкой минимального контраста называется
. Оценкой минимального контраста называется
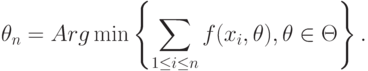
Если множество 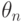 состоит из более чем одного элемента, то оценкой минимального контраста называют также любой элемент
состоит из более чем одного элемента, то оценкой минимального контраста называют также любой элемент 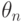 .
.
Оценками минимального контраста являются, в частности, многие робастные статистики [
[
1.15
]
,
[
12.45
]
]. Эти оценки широко используются в статистике объектов нечисловой природы [
[
1.15
]
,
[
12.38
]
], поскольку при  переходят в эмпирические средние, а если
переходят в эмпирические средние, а если  - пространство бинарных отношений - в медиану Кемени.
- пространство бинарных отношений - в медиану Кемени.
Пусть в  имеется мера
имеется мера 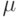 (заданная на той же
(заданная на той же  -алгебре, что участвует в определении случайных элементов
-алгебре, что участвует в определении случайных элементов  ), и
), и  - плотность распределения
- плотность распределения  по мере
по мере 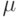 . Если
. Если

Асимптотическое поведение оценок минимального контраста в случае пространств  и
и  общего вида хорошо изучено [
[
12.25
]
], в частности, известны условия состоятельности оценок. Здесь ограничимся случаем
общего вида хорошо изучено [
[
12.25
]
], в частности, известны условия состоятельности оценок. Здесь ограничимся случаем  , но при этом введя погрешности измерений
, но при этом введя погрешности измерений 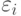 . Примем также, что
. Примем также, что  .
.
В рассматриваемой математической модели предполагается, что статистику известны лишь искаженные значения 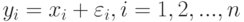 . Поэтому вместо
. Поэтому вместо 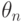 он вычисляет
он вычисляет

Будем изучать величину  в предположении, что погрешности измерений
в предположении, что погрешности измерений 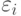 малы. Цель этого изучения - продемонстрировать идеи статистики интервальных данных при достаточно простых предположениях. Поэтому естественно следовать условиям и ходу рассуждений, которые обычно принимаются при изучении оценок максимального правдоподобия [
[
2.10
]
, п.33.3].
малы. Цель этого изучения - продемонстрировать идеи статистики интервальных данных при достаточно простых предположениях. Поэтому естественно следовать условиям и ходу рассуждений, которые обычно принимаются при изучении оценок максимального правдоподобия [
[
2.10
]
, п.33.3].
Пусть 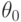 - истинное значение параметра, функция f(x;\theta) трижды дифференцируема по
- истинное значение параметра, функция f(x;\theta) трижды дифференцируема по 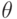 , причем
, причем
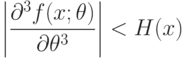
 . Тогда
. Тогда |
( 27) |
 .
.Используя обозначения векторов 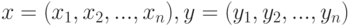 , введем суммы
, введем суммы
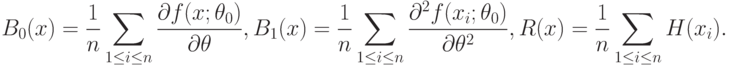
Аналогичным образом введем функции  , в которых вместо
, в которых вместо  стоят
стоят 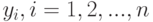 .
.
Поскольку в соответствии с теоремой Ферма оценка минимального контраста 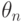 удовлетворяет уравнению
удовлетворяет уравнению
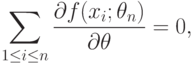 |
( 28) |
 вместо
вместо  и суммируя по
и суммируя по 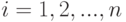 , получаем, что
, получаем, что |
( 29) |
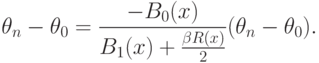 |
( 30) |
Решения уравнения (28) будем также называть оценками минимального контраста. Хотя уравнение (28) - лишь необходимое условие минимума, такое словоупотребление не будет вызывать трудностей.
Теорема 1. Пусть для любого  выполнено соотношение (27). Пусть для случайной величины
выполнено соотношение (27). Пусть для случайной величины  с распределением, соответствующим значению параметра
с распределением, соответствующим значению параметра  , существуют математические ожидания
, существуют математические ожидания
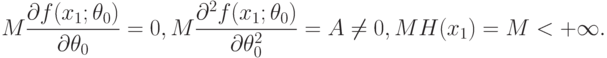 |
( 31) |
Тогда существуют оценки минимального контраста 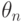 такие, что
такие, что  при
при 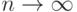 (в смысле сходимости по вероятности).
(в смысле сходимости по вероятности).
Доказательство. Возьмем 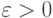 и
и 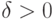 . В силу закона больших чисел (теорема Хинчина) существует
. В силу закона больших чисел (теорема Хинчина) существует  такое, что для любого
такое, что для любого 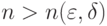 справедливы неравенства
справедливы неравенства

Тогда с вероятностью не менее 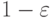 одновременно выполняются соотношения
одновременно выполняются соотношения
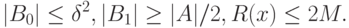 |
( 32) |
При ![\theta\in[\theta_0-\delta;\theta_0+\delta]](/sites/default/files/tex_cache/ab2f5ecbe28fd02a239849765284193b.png) рассмотрим многочлен второй степени
рассмотрим многочлен второй степени
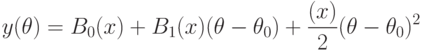
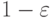 выполнены соотношения
выполнены соотношения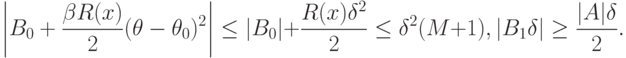
Если  , то знак
, то знак  в точках
в точках 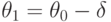 и
и  определяется знаком линейного члена
определяется знаком линейного члена 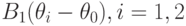 , следовательно, знаки
, следовательно, знаки 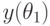 и
и  различны, а потому существует
различны, а потому существует ![\theta_n\in[\theta_0-\delta;\theta_0+\delta]](/sites/default/files/tex_cache/8a82e640b5028ef0c7e015f4d5b13436.png) такое, что
такое, что  , что и требовалось доказать.
, что и требовалось доказать.
Теорема 2. Пусть выполнены условия теоремы 1 и, кроме того, для случайной величины  , распределение которой соответствует значению параметра
, распределение которой соответствует значению параметра  , существует математическое ожидание
, существует математическое ожидание
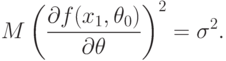
Тогда оценка минимального контраста имеет асимптотически нормальное распределение:
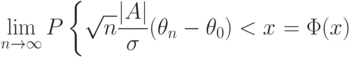 |
( 33) |
для любого  , где
, где 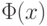 - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
Доказательство. Из центральной предельной теоремы вытекает, что числитель в правой части формулы (30) асимптотически нормален с математическим ожиданием 0 и дисперсией 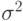 . Первое слагаемое в знаменателе формулы (30) в силу условий (31) и закона больших чисел сходится по вероятности к
. Первое слагаемое в знаменателе формулы (30) в силу условий (31) и закона больших чисел сходится по вероятности к 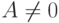 , а второе слагаемое по тем же основаниям и с учетом теоремы 1 - к 0. Итак, знаменатель сходится по вероятности к
, а второе слагаемое по тем же основаниям и с учетом теоремы 1 - к 0. Итак, знаменатель сходится по вероятности к 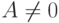 . Доказательство теоремы 2 завершает ссылка на теорему о наследовании сходимости (4.3 и [
[
1.15
]
,
. Доказательство теоремы 2 завершает ссылка на теорему о наследовании сходимости (4.3 и [
[
1.15
]
,  2.4]).
2.4]).
Нотна оценки минимального контраста. Аналогично (30) нетрудно получить, что
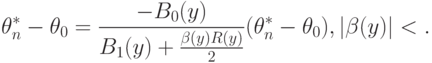 |
( 34) |
Следовательно,  есть разность правых частей формул (30) и (34). Найдем максимально возможное значение (т.е. нотну) величины при ограничениях (1) на абсолютные погрешности результатов измерений.
есть разность правых частей формул (30) и (34). Найдем максимально возможное значение (т.е. нотну) величины при ограничениях (1) на абсолютные погрешности результатов измерений.
Покажем, что при  для некоторого
для некоторого 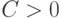 нотна имеет вид
нотна имеет вид
 |
( 35) |
Поскольку 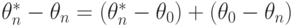 , то из (33) и (35) следует, что
, то из (33) и (35) следует, что
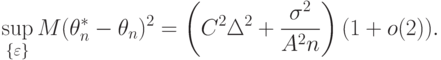 |
( 36) |
Можно сказать, что наличие погрешностей 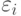 приводит к появлению систематической ошибки (смещения) у оценки метода максимального правдоподобия, и нотна является максимально возможным значением этой систематической ошибки.
приводит к появлению систематической ошибки (смещения) у оценки метода максимального правдоподобия, и нотна является максимально возможным значением этой систематической ошибки.
В правой части (36) первое слагаемое - квадрат асимптотической нотны, второе соответствует статистической ошибке. Приравнивая их, получаем рациональный объем выборки

Остается доказать соотношение (35) и вычислить  . Укажем сначала условия, при которых
. Укажем сначала условия, при которых  (по вероятности) при
(по вероятности) при 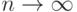 одновременно с
одновременно с  .
.
Теорема 3. Пусть существуют константа  и функции
и функции  такие, что при
такие, что при 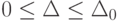 и
и 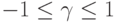 выполнены неравенства (ср. формулу (27))
выполнены неравенства (ср. формулу (27))
 |
( 37) |
 . Пусть для случайной величины
. Пусть для случайной величины  , распределение которой соответствует
, распределение которой соответствует  , существуют
, существуют  и
и 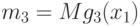 . Пусть выполнены условия теоремы 1. Тогда
. Пусть выполнены условия теоремы 1. Тогда  (по вероятности) при
(по вероятности) при 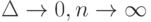 .
.Доказательство проведем по схеме доказательства теоремы 1. Из неравенств (37) вытекает, что
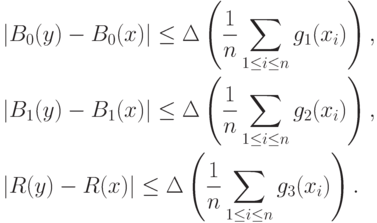 |
( 38) |
Возьмем 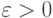 и
и 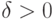 . В силу закона больших чисел (теорема Хинчина) существует
. В силу закона больших чисел (теорема Хинчина) существует  такое, что для любого
такое, что для любого 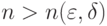 справедливы неравенства
справедливы неравенства
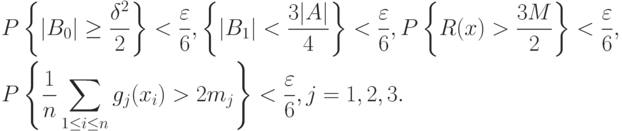
Тогда с вероятностью не менее 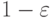 одновременно выполняются соотношения
одновременно выполняются соотношения

В силу (38) при этом

Пусть
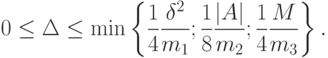
Тогда с вероятностью не менее 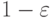 одновременно выполняются соотношения (ср. (32))
одновременно выполняются соотношения (ср. (32))

Завершается доказательство дословным повторением такового в теореме 1, с единственным отличием - заменой в обозначениях  на
на  .
.
Теорема 4. Пусть выполнены условия теоремы 3 и, кроме того, существуют математические ожидания (при  )
)
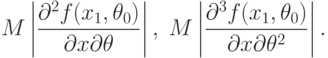 |
( 39) |
Тогда выполнено соотношение (35) с
 |
( 40) |
Доказательство. Воспользуемся следующим элементарным соотношением. Пусть  и
и  - бесконечно малые по сравнению с
- бесконечно малые по сравнению с 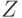 и
и  соответственно. Тогда с точностью до бесконечно малых более высокого порядка
соответственно. Тогда с точностью до бесконечно малых более высокого порядка
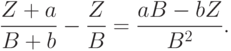
Чтобы применить это соотношение к анализу  в соответствии с (30), (34) и теоремой 2, положим
в соответствии с (30), (34) и теоремой 2, положим
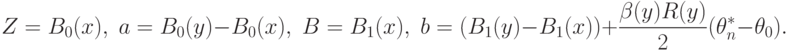
В силу условий теоремы 4 при малых 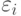 с точностью до членов более высокого порядка
с точностью до членов более высокого порядка

При  эти величины бесконечно малы, а потому с учетом сходимости
эти величины бесконечно малы, а потому с учетом сходимости 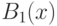 к
к  и теоремы 3
и теоремы 3
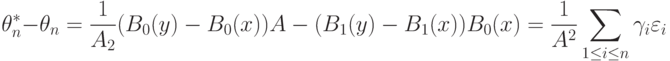

Ясно, что задача оптимизации
 |
( 41) |

 . Поэтому
. Поэтому |
( 42) |
С целью упрощения правой части (42) воспользуемся тем, что
 |
( 43) |
 .
.Поскольку при 
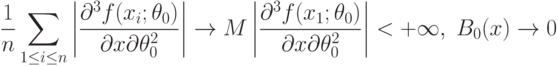
 , где
, где  определено в (40). Теорема 4 доказана.
определено в (40). Теорема 4 доказана.Оценки метода моментов. Пусть 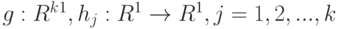 , - некоторые функции. Рассмотрим аналоги выборочных моментов
, - некоторые функции. Рассмотрим аналоги выборочных моментов
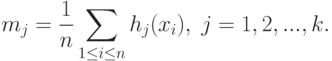
Оценки метода моментов имеют вид
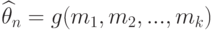
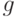 и
и 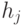 должны удовлетворять некоторым дополнительным условиям [
[
12.3
]
, с.80], которые здесь не приводим). Очевидно, что
должны удовлетворять некоторым дополнительным условиям [
[
12.3
]
, с.80], которые здесь не приводим). Очевидно, что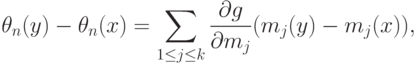
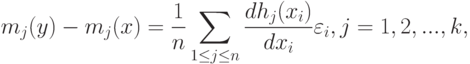 |
( 44) |
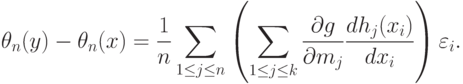 |
( 45) |
Теорема 5. Пусть при  существуют математические ожидания
существуют математические ожидания
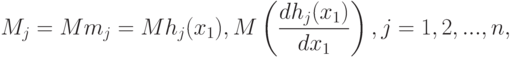
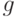 дважды непрерывно дифференцируема в некоторой окрестности точки
дважды непрерывно дифференцируема в некоторой окрестности точки 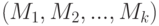 . Пусть существует функция
. Пусть существует функция 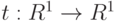 такая, что
такая, что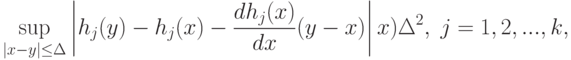 |
( 46) |
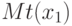 существует. Тогда
существует. Тогда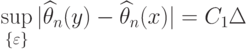
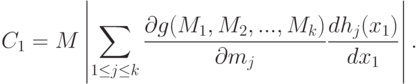
Доказательство теоремы 5 сводится к обоснованию проведенных ранее рассуждений, позволивших получить формулу (45). В условиях теоремы 5 собраны предположения, достаточные для такого обоснования. Так, условие (46) дает возможность обосновать соотношения (44); существование  обеспечивает существование
обеспечивает существование 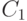 , и т.д. Завершает доказательство ссылка на решение задачи оптимизации (41) и применение закона больших чисел.
, и т.д. Завершает доказательство ссылка на решение задачи оптимизации (41) и применение закона больших чисел.
Полученные в теоремах 4 и 5 нотны оценок минимального контраста и метода моментов, асимптотические дисперсии этих оценок (см. теорему 2 и [
[
12.17
]
] соответственно) позволяют находить рациональные объемы выборок, строить доверительные интервалы с учетом погрешностей измерений, а также сравнивать оценки по среднему квадрату ошибки (36). Подобное сравнение было проведено для оценок максимального правдоподобия и метода моментов параметров гамма-распределения. Установлено, что классический вывод о преимуществе оценок максимального правдоподобия [
[
1.7
]
, с.99-100] неверен в случае 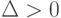 .
.
