|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистика нечисловых данных
11.4. Метод парных сравнений
Пример практического применения метода парных сравнений. Деятельность предприятия по реализации услуг всегда сопряжена с рядом проблем, от качества решения которых зависит его будущее. Руководителю службы маркетинга необходимо знать факторы, сдерживающие продажи, и оценить степень важности каждого из них. При кажущейся очевидности и простоте решения далеко не вся управленческая команда дает однозначный ответ: какая из проблем на текущий момент является наиболее важной. Необходим экспертный опрос на эту тему.
Целью исследования факторов, влияющих на объемы продаж, является их ранжирование по степени важности. Для этого среди 25 сотрудников отдела сбыта, а также 10 руководителей завода ГАРО (Великий Новгород) А.А. Пивнем был проведен опрос, в котором предлагалось сравнить попарно факторы, определив более важный среди двух. Итог определялся как среднее арифметическое сумм баллов, набранных каждым фактором у всех опрашиваемых.
Были проанализированы следующие 15 факторов:
- потребительские свойства изделий (качество, надежность, показатели назначения и т.д.);
- уровень цен;
- срок поставки продукции;
- информация о предлагаемых к продаже изделиях;
- уровень гарантийного и сервисного обслуживания;
- работа дилеров, представительств;
- рекламная деятельность;
- численность персонала;
- мотивация труда;
- инициативность персонала;
- маркетинговая деятельность;
- оснащенность техническими средствами;
- квалификация персонала;
- корпоративная культура;
- репутация компании.
В результате анализа результатов парных сравнений построена структурная схема, показывающая степень влияния факторов на объемы продаж ( рис. 11.1).
Наибольшую значимость на сегодняшний день имеет срок поставки продукции и квалификация персонала. Меняются подходы к продвижению товаров на рынке. Ранее успешно применяемые способы продаж (почтовая рассылка рекламы, участие в специализированных выставках, публикации в газетах и специализированных изданиях, конференции и т.д.) сегодня требуют иного качественного подхода. Срок поставки продукции, как правило, связан с производственно-технологическим циклом изготовления и настройки изделий. Мотивация труда, равно как и уровень гарантийного и сервисного обслуживания, имеют также большое значение. Разрабатывается и утверждается новая система оплаты труда, которая позволяет устранить возникающие противоречия. Отдел сервисного обслуживания гаражного оборудования должен разработать концепцию развития сервисной сети с целью наиболее полного удовлетворения потребителя, а значит и завоевания преимуществ в конкурентной борьбе.
Среди проблем более низкого уровня значимости необходимо отметить место корпоративной культуры. Понимание и осознание себя, как части сплоченного коллектива - сложный процесс. Достижение синергетического эффекта возможно только в коллективе, в котором отдельный сотрудник понимает и делает свою работу через понимание целей и задач всей компании. Формированию корпоративной культуры следует уделить особое внимание.
Проведенный анализ дает возможность компании сосредоточить свои усилия на наиболее важных на данный момент обозначенных проблемах. Выбор пути решения каждой из них определяется возможностями компании и опытом руководителей.
Вероятностное моделирование парных сравнений. Напомним общую модель парных сравнений, введенную в 5.4.
Пусть  объектов
объектов 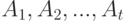 сравниваются попарно каждым из
сравниваются попарно каждым из  экспертов. Следовательно, возможных пар для сравнения имеется
экспертов. Следовательно, возможных пар для сравнения имеется 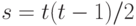 . Эксперт с номером
. Эксперт с номером  делает
делает 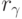 повторных сравнений для каждой из
повторных сравнений для каждой из  возможностей. Пусть
возможностей. Пусть 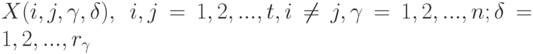 , - случайная величина, принимающая значения 1 или 0 в зависимости от того, предпочитает ли эксперт
, - случайная величина, принимающая значения 1 или 0 в зависимости от того, предпочитает ли эксперт  объект
объект  или объект
или объект 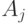 в
в  -м сравнении двух объектов. Обычно принимают, что все сравнения проводятся независимо друг от друга, так что случайные величины
-м сравнении двух объектов. Обычно принимают, что все сравнения проводятся независимо друг от друга, так что случайные величины 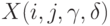 независимы в совокупности, если не считать того, что
независимы в совокупности, если не считать того, что 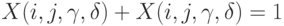 . Положим
. Положим
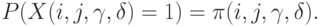
Ясно, что описанная модель парных сравнений представляет собой частный случай люсиана (в другой терминологии - бернуллиевского вектора). В этой модели число наблюдений равно числу неизвестных параметров, поэтому для получения статистических выводов необходимо наложить те или иные априорные условия на 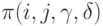 , например:
, например:
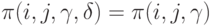 (нет эффекта от повторений);
(нет эффекта от повторений);
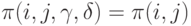 (нет эффекта от повторений и от экспертов).
(нет эффекта от повторений и от экспертов).
Теорию независимых парных сравнений целесообразно разделить на две части - непараметрическую, в которой статистические задачи ставятся непосредственно в терминах 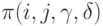 , и параметрическую, в которой вероятности
, и параметрическую, в которой вероятности 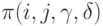 выражаются через меньшее число иных параметров. Ряд результатов непараметрической теории парных сравнений непосредственно вытекает из теории люсианов.
выражаются через меньшее число иных параметров. Ряд результатов непараметрической теории парных сравнений непосредственно вытекает из теории люсианов.
В параметрической теории парных сравнений наиболее популярна линейная модель, в которой предполагается, что каждому объекту  можно приписать некоторую "ценность"
можно приписать некоторую "ценность" 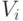 так, что вероятность предпочтения
так, что вероятность предпочтения 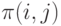 (т.е. предполагается дополнительно, что эффект от повторений и от экспертов отсутствует) будет выражаться следующим образом:
(т.е. предполагается дополнительно, что эффект от повторений и от экспертов отсутствует) будет выражаться следующим образом:
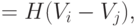 |
( 1) |
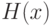 - функция распределения, симметричная относительно 0, т.е.
- функция распределения, симметричная относительно 0, т.е.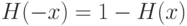 |
( 2) |
 .
.Широко применяются модели Терстоуна-Мостеллера и Брэдли-Терри, в которых 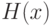 - соответственно функции нормального и логистического распределений. С прикладной точки зрения эти две модели практически совпадают. Действительно, поскольку функция
- соответственно функции нормального и логистического распределений. С прикладной точки зрения эти две модели практически совпадают. Действительно, поскольку функция  стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1 и функция
стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1 и функция
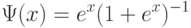

Соотношение (1) вытекает из следующей модели поведения эксперта: он измеряет "ценность" 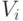 и
и 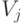 объектов
объектов  и
и 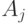 , но с ошибками
, но с ошибками 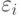 и
и 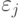 соответственно, а затем сравнивает свои оценки ценности объектов
соответственно, а затем сравнивает свои оценки ценности объектов 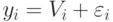 и
и 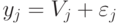 . Если
. Если 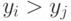 то он предпочитает
то он предпочитает  , в противном случае -
, в противном случае - 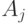 . Тогда
. Тогда
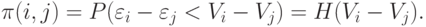 |
( 3) |
Обычно предполагают, что субъективные ошибки эксперта и независимы и имеют одно и то же непрерывное распределение. Тогда функция распределения 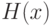 из соотношения (3) непрерывна и удовлетворяет функциональному уравнению (2).
из соотношения (3) непрерывна и удовлетворяет функциональному уравнению (2).
Пример. При опросе экспертов (август 2001 г.) попарно сравнивались четыре компании ТНК, Лукойл, Юкос, Татнефть, продающие автомобильное топливо. Сравнение проводилось по качеству бензина. При 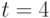 пар для сравнения имеется
пар для сравнения имеется 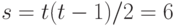 .
.
Результаты парных сравнений приведены в табл.1. По ним необходимо определить взаимное положение четырех компаний на оси "качество бензина", т.е. найти их "ценности"  .
.
| Пары | Частота выбора первого элемента пары | Частота выбора второго элемента пары |
|---|---|---|
| ТНК - Лукойл |  |
 |
| ТНК - Юкос |  |
 |
| ТНК - Татнефть |  |
 |
| Лукойл - Юкос |  |
 |
| Лукойл - Татнефть |  |
 |
| Юкос - Татнефть |  |
 |
Применим модель Терстоуна-Мостеллера, согласно которой погрешности мнений экспертов 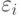 являются независимыми нормально распределенными случайными величинами с нулевым математическим ожиданием и дисперсией
являются независимыми нормально распределенными случайными величинами с нулевым математическим ожиданием и дисперсией  .
.
Легко видеть, что "ценности"  измерены в шкале интервалов. Начало координат можно выбрать произвольно, поскольку вероятности результатов сравнения зависят только от попарных разностей "ценностей"
измерены в шкале интервалов. Начало координат можно выбрать произвольно, поскольку вероятности результатов сравнения зависят только от попарных разностей "ценностей"  . Например, можно положить
. Например, можно положить 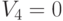 . Единицу измерения также можно выбрать произвольно. При изменении единицы измерения меняется
. Единицу измерения также можно выбрать произвольно. При изменении единицы измерения меняется  , точнее, единица измерения однозначно связана с величиной
, точнее, единица измерения однозначно связана с величиной  . Дисперсия разности
. Дисперсия разности 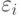 -
- 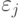 равна
равна  . В соответствии с формулой (3) удобно выбрать единицу измерения так, чтобы
. В соответствии с формулой (3) удобно выбрать единицу измерения так, чтобы 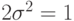 , т.е.
, т.е. 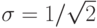 . Тогда
. Тогда  в формуле (3) - это функция
в формуле (3) - это функция  стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.
В соответствии с (3) имеем систему шести уравнений с тремя неизвестными:
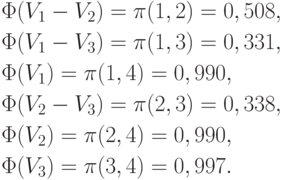
Применяя к каждому их этих уравнений преобразование 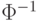 , получаем систему шести линейных уравнений с тремя неизвестными:
, получаем систему шести линейных уравнений с тремя неизвестными:
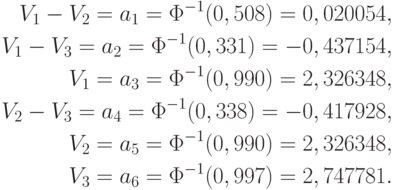
(Значения 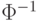 взяты из таблицы 1.3 сборника [
[
2.1
]
].)
взяты из таблицы 1.3 сборника [
[
2.1
]
].)
В полученной системе число уравнений больше числа неизвестных, т.е. система переопределена. Дальнейшие расчеты могут проводиться разными способами. Простейший из них состоит в том, чтобы выбрать три уравнения, а именно, третье, пятое и шестое, которые и дают искомые значения:

Таким образом, качество бензина лучше всего у Юкоса, оно несколько хуже у ТНК и Лукойла, одинаковых по этому показателю, а у Татнефти - значительно хуже тройки лидеров. Можно показать, что если модель Терстоуна-Мостеллера верна и число экспертов достаточно велико, то отбрасывание "лишних" уравнений является корректным способом обработки экспертных данных, поскольку дает состоятельные оценки "ценностей" 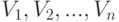 .
.
Однако ясно, что при отбрасывании трех уравнений из шести часть информации теряется. Например, первое уравнение показывает, что по мнению экспертов качество бензина у ТНК несколько лучше, чем у Лукойла. Поэтому целесообразно применить метод наименьших квадратов для оценивания  . А именно, рассмотрим функцию трех переменных
. А именно, рассмотрим функцию трех переменных

Оценки по методу наименьших квадратов - это результат минимизации функции 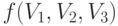 по совокупности переменных
по совокупности переменных 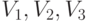 . Как и в
"Многомерный статистический анализ"
, для минимизации этой функции достаточно приравнять 0 частные производные этой функции по
. Как и в
"Многомерный статистический анализ"
, для минимизации этой функции достаточно приравнять 0 частные производные этой функции по 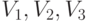 . Имеем:
. Имеем:
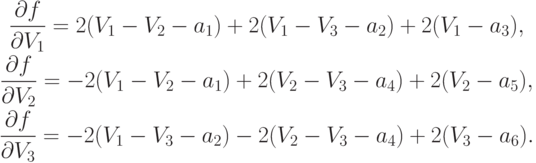
Приравнивая частные производные 0, деля на 2, раскрывая скобки и перенося свободные члены в правую часть, получаем систему трех линейных уравнений с тремя неизвестными
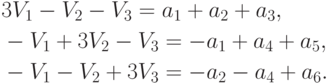
Решение этой системы не представляет трудностей.
Вообще говоря, не всегда сравниваемые объекты можно представить точками на прямой, т.е. не всегда их можно линейно упорядочить. Возможно, более соответствует данным опроса экспертов представление объектов точками на плоскости или в пространстве большей размерности. В статистике парных сравнений [ [ 1.5 ] ] разработаны методы проверки адекватности модели Терстоуна-Мостеллера и других параметрических моделей. Для этого обычно используются статистики типа хи-квадрат.

