|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистика нечисловых данных
11.3. Теория люсианов
Асимптотика растущей размерности и проверяемые гипотезы. Продолжим изучение модели порождения данных (6) - (7) предыдущего параграфа. Будем использовать асимптотику  . При этом число неизвестных параметров растет пропорционально объему данных.
. При этом число неизвестных параметров растет пропорционально объему данных.
В последние десятилетия (с начала 1970-х годов) в прикладной статистике все большее распространение получают постановки, в которых число неизвестных параметров растет вместе с объемом выборки. Результаты, полученные в подобных постановках, называют найденными "в асимптотике растущей размерности" или "в асимптотике А.Н.Колмогорова" [ [ 5.15 ] ], перенося терминологию исследований по дискриминантному анализу на общий случай. Как известно, в задаче дискриминации в две совокупности академик АН СССР А.Н. Колмогоров (1903 - 1987) предложил рассматривать асимптотику
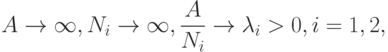
 - размерность пространства (число признаков),
- размерность пространства (число признаков),  - объемы обучающих выборок,
- объемы обучающих выборок, 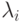 - константы,
- константы, 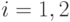 . Эта асимптотика естественна при обработке организационно-экономических, социологических, медицинских данных, поскольку число признаков, определяемых для каждого изучаемого объекта, респондента или пациента, обычно имеет тот же порядок, что и объем выборки.
. Эта асимптотика естественна при обработке организационно-экономических, социологических, медицинских данных, поскольку число признаков, определяемых для каждого изучаемого объекта, респондента или пациента, обычно имеет тот же порядок, что и объем выборки.Пусть  - независимые (между собой) люсианы с векторами параметров
- независимые (между собой) люсианы с векторами параметров  соответственно. Гипотезой согласованности будем называть гипотезу
соответственно. Гипотезой согласованности будем называть гипотезу
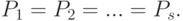 |
( 1) |
Для ранжировок и разбиений под согласованностью понимают более частную гипотезу, предполагающую отрицание равномерности распределений (т.е. одинаковой вероятности появления каждой возможной ранжировки или разбиения), что соответствует замене проверки гипотезы (1) на проверку гипотезы
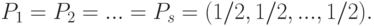 |
( 2) |
Как разъяснено в [ [ 1.15 ] , [ 11.21 ] ], гипотеза (1) более адекватна конкретным задачам обработки реальных данных, например, экспертных оценок, чем (2). Поэтому полученные от экспертов данные, содержащие противоречия, целесообразно рассматривать как люсианы и проверять гипотезу (1), а не подбирать ближайшие ранжировки или разбиения, после чего проверять согласованность методами теории случайных ранжировок или разбиений, как иногда рекомендуется.
Пусть  и
и  - независимые в совокупности люсианы длины
- независимые в совокупности люсианы длины  , одинаково распределенные в каждой группе с параметрами
, одинаково распределенные в каждой группе с параметрами 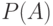 и
и 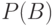 соответственно. Гипотезой однородности называется гипотеза
соответственно. Гипотезой однородности называется гипотеза

В асимптотике растущей размерности принимаем, что  и
и  постоянны, а
постоянны, а 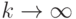 .
.
Пусть  - последовательность (фиксированной длины) пар люсианов. Пары предполагаются независимыми между собой. Требуется проверить гипотезу независимости
- последовательность (фиксированной длины) пар люсианов. Пары предполагаются независимыми между собой. Требуется проверить гипотезу независимости  и
и  , т.е. внутри пар. В ранее введенных обозначениях гипотеза независимости - это гипотеза
, т.е. внутри пар. В ранее введенных обозначениях гипотеза независимости - это гипотеза
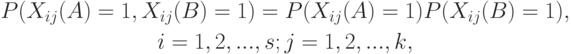
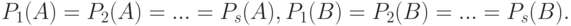
В настоящем параграфе излагается метод проверки гипотез о люсианах в асимптотике растущей размерности на примере гипотезы согласованности. Эти результаты получены в [ [ 1.15 ] , [ 5.13 ] , [ 5.15 ] ]. Дальнейшее изучение проведено нашими учениками Г.В. Рыдановой, Т.Н. Дылько, Г.В. Раушенбахом, О.В. Филипповым, А.М. Никифоровым и др. Гипотеза однородности рассмотрена, например, в [ [ 5.13 ] ]. Методы проверки гипотезы однородности люсианов развиты и изучены Г.В. Рыдановой [ [ 11.34 ] ] на основе описанного ниже подхода. Она, помимо доказательства предельных теорем, подробно изучила скорость сходимости методом статистических испытаний.
Методы проверки согласованности люсианов нашли практическое применение, в частности, в медицине. Они были использованы в кардиологии при анализе данных кинетотопографии [ [ 11.1 ] , [ 5.13 ] , [ 11.32 ] ]. Эти методы включены в методические рекомендации Академии медицинских наук СССР и Ученого медицинского совета Минздрава СССР по управлению научными медицинскими исследованиями [ [ 11.18 ] ].
 . Будем использовать дальнейшее развитие метода, описанного в 7.4. Почему нельзя использовать иные подходы, имеющиеся в математической статистике? Поскольку число неизвестных параметров растет вместе с объемом выборки и пропорционально ему, эти параметры не являются мешающими. Отметим, что согласно [
[
11.13
]
] равномерно наиболее мощных критериев не существует, поскольку параметров много. Не останавливаясь на других подходах математической статистики, констатируем необходимость применения метода проверки гипотез по совокупности малых выборок.
. Будем использовать дальнейшее развитие метода, описанного в 7.4. Почему нельзя использовать иные подходы, имеющиеся в математической статистике? Поскольку число неизвестных параметров растет вместе с объемом выборки и пропорционально ему, эти параметры не являются мешающими. Отметим, что согласно [
[
11.13
]
] равномерно наиболее мощных критериев не существует, поскольку параметров много. Не останавливаясь на других подходах математической статистики, констатируем необходимость применения метода проверки гипотез по совокупности малых выборок.
Пусть имеются  выборок, независимых между собой. Пусть при справедливости нулевой гипотезы по каждой из выборок можно построить несмещенную оценку
выборок, независимых между собой. Пусть при справедливости нулевой гипотезы по каждой из выборок можно построить несмещенную оценку 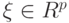 векторного нуля
векторного нуля 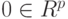 , где
, где  . Другими словами, пусть распределение
. Другими словами, пусть распределение  -ой выборки описывается параметром
-ой выборки описывается параметром 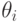 , лежащим в произвольном пространстве, а нулевая гипотеза, очевидно, состоит в том, что
, лежащим в произвольном пространстве, а нулевая гипотеза, очевидно, состоит в том, что  , где
, где  - собственное подмножество множества
- собственное подмножество множества  . Предполагается, что можно по
. Предполагается, что можно по  -ой выборке вычислить статистику
-ой выборке вычислить статистику 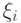 такую, что
такую, что
 |
( 3) |
 . Очевидно,
. Очевидно,  удовлетворяют (3). Однако для рассматриваемого метода необходимо, чтобы при всех
удовлетворяют (3). Однако для рассматриваемого метода необходимо, чтобы при всех  ковариационная матрица вектора
ковариационная матрица вектора 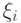 была ненулевой:
была ненулевой: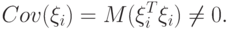 |
( 4) |
В теории математической статистики иногда используют понятие полноты параметрического семейства распределений. Если рассматриваемое семейство является полным - а так и есть для люсианов, - то не существует достаточной статистики, удовлетворяющей одновременно условиям (3) и (4) (см., например, [
[
11.4
]
, 
 2.12-2.14]). Поэтому будем использовать статистики, не являющиеся достаточными.
2.12-2.14]). Поэтому будем использовать статистики, не являющиеся достаточными.
Следующее предположение - ковариационные матрицы статистик 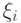 , т.е.
, т.е.  , также допускают несмещенные оценки
, также допускают несмещенные оценки 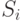 по тем же выборкам:
по тем же выборкам:
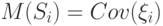 |
( 5) |
 .
.Рассматриваемый метод основан на том, что поскольку случайные векторы 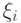 определяются по независимым между собой выборкам, то
определяются по независимым между собой выборкам, то 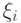 независимы в совокупности, а потому случайный вектор
независимы в совокупности, а потому случайный вектор
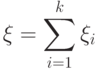 |
( 6) |

При справедливости многомерной центральной предельной теоремы (простейшее условие справедливости этой теоремы для 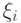 в случае люсианов - отделенность от 0 и 1 всех элементов матриц
в случае люсианов - отделенность от 0 и 1 всех элементов матриц 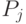 , равномерная по
, равномерная по  и
и  ) вектор
) вектор  является асимптотически нормальным, т.е. при
является асимптотически нормальным, т.е. при 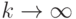 распределение
распределение  сближается (в смысле, раскрытом в
"Теоретическая база прикладной статистики"
) с многомерным нормальным распределением
сближается (в смысле, раскрытом в
"Теоретическая база прикладной статистики"
) с многомерным нормальным распределением 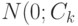 ).
).
Однако эту сходимость нельзя непосредственно использовать для проверки исходной гипотезы, поскольку матрица  неизвестна статистику. Необходимо оценить эту матрицу по статистическим данным. В силу (5) в качестве оценки
неизвестна статистику. Необходимо оценить эту матрицу по статистическим данным. В силу (5) в качестве оценки  естественно использовать
естественно использовать
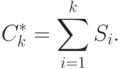
Простейшая формулировка условий справедливости такой замены - предположение о том, что к последовательности 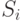 можно применить закон больших чисел. А именно, пусть существует неотрицательно определенная матрица
можно применить закон больших чисел. А именно, пусть существует неотрицательно определенная матрица  такая, что при
такая, что при 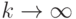
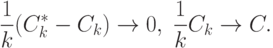 |
( 7) |
В силу результатов
"Теоретическая база прикладной статистики"
из асимптотической нормальности  и соотношений (7) следует, что распределение статистики
и соотношений (7) следует, что распределение статистики

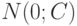 . При этом, если некоторый случайный вектор
. При этом, если некоторый случайный вектор  имеет распределение
имеет распределение 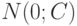 , то распределение случайной величины
, то распределение случайной величины 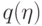 сходится к распределению
сходится к распределению  для произвольной интегрируемой по Риману по любому кубу функции
для произвольной интегрируемой по Риману по любому кубу функции  . Для проверки нулевой гипотезы предлагается пользоваться статистикой
. Для проверки нулевой гипотезы предлагается пользоваться статистикой 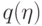 при подходящей функции
при подходящей функции  , а процентные точки брать соответственно распределению
, а процентные точки брать соответственно распределению  . В этом и состоит рассматриваемый метод проверки гипотез о люсианах в асимптотике растущей размерности. Для реальных расчетов целесообразно использовать линейные или квадратические функции
. В этом и состоит рассматриваемый метод проверки гипотез о люсианах в асимптотике растущей размерности. Для реальных расчетов целесообразно использовать линейные или квадратические функции  от координат вектора
от координат вектора  .
.Отклонения от нулевой гипотезы приводят, как правило, к нарушению равенств (3) и (4). Случайный вектор ? при этом обычно остается асимптотически нормальным, но с другими параметрами, что может быть обычным образом использовано для построения оптимального решающего правила, соответствующего заданной альтернативе (например, согласно лемме Неймана-Пирсона). Поведение при альтернативах для некоторых гипотез изучено в [  ,
,  ], здесь его не будем рассматривать, поскольку вычисление мощности не требует новых идей.
], здесь его не будем рассматривать, поскольку вычисление мощности не требует новых идей.
Несмещенные оценки параметров асимптотического распределения вектора попарных расстояний. Применим описанный выше метод для проверки гипотезы согласованности люсианов. Исходные данные - люсианы
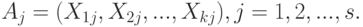
В качестве  -й выборки возьмем совокупность испытаний Бернулли, стоящих на
-й выборки возьмем совокупность испытаний Бернулли, стоящих на  -м месте в рассматриваемых люсианах:
-м месте в рассматриваемых люсианах:
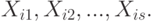 |
( 8) |
При справедливости нулевой гипотезы в (8) стоят независимые испытания Бернулли с одной и той же вероятностью успеха 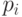 ; при нарушении нулевой гипотезы согласованности независимость испытаний Бернулли сохраняется, но вероятности успеха могут различаться.
; при нарушении нулевой гипотезы согласованности независимость испытаний Бернулли сохраняется, но вероятности успеха могут различаться.
В качестве вектора  , на основе которого строятся статистики для проверки согласованности, будем использовать вектор попарных расстояний между люсианами
, на основе которого строятся статистики для проверки согласованности, будем использовать вектор попарных расстояний между люсианами
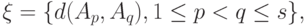 |
( 9) |
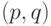 упорядочены лексикографически,
упорядочены лексикографически,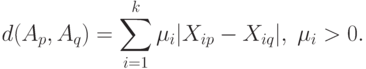 |
( 10) |
В
"Различные виды статистических данных"
это расстояние выведено из некоторой системы аксиом (напомним, что совокупность векторов из 0 и 1 размерности  находится во взаимнооднозначном соответствии с совокупностью подмножеств множества из
находится во взаимнооднозначном соответствии с совокупностью подмножеств множества из  элементов; при этом 1 соответствует тому, что элемент входит в подмножество, а 0 - что не входит).
элементов; при этом 1 соответствует тому, что элемент входит в подмножество, а 0 - что не входит).
Из вида расстояния в формуле (10) следует, что введенный в (9) вектор  имеет вид (6) с
имеет вид (6) с
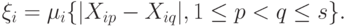 |
( 11) |
Следовательно, для применения описанного выше метода проверки гипотез о люсианах в асимптотике растущей размерности достаточно построить на основе вектора 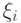 из (11) несмещенную оценку 0 и найти несмещенную оценку ковариационной матрицы этой оценки.
из (11) несмещенную оценку 0 и найти несмещенную оценку ковариационной матрицы этой оценки.
Чтобы применить общую схему, необходимо начать с построения статистики  такой, чтобы при всех
такой, чтобы при всех 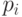 имело место равенство
имело место равенство

Элементарный расчет дает:
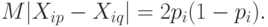
Как известно [ [ 11.14 ] , с.56-57], несмещенная оценка многочлена
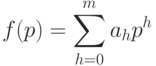
 независимых испытаний Бернулли с вероятностью успеха
независимых испытаний Бернулли с вероятностью успеха  в каждом имеет вид
в каждом имеет вид![f^*(p)=\sum_{h=0}^m a_h\frac{\gamma^{[h]}}{m^{[h]}},](/sites/default/files/tex_cache/d18a8a8e1e801483de43c6758314dc61.png) |
( 12) |
 - общее число успехов в
- общее число успехов в  испытаниях и использовано обозначение
испытаниях и использовано обозначение![n^{[h]} = n(n - 1)...(n - h + 1).](/sites/default/files/tex_cache/4511e6e65c66201b187b3de409c1f3c8.png)
Ясно, что многочлены степени 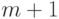 и более высокой невозможно несмещенно оценить по результатам
и более высокой невозможно несмещенно оценить по результатам  испытаний.
испытаний.
В случае 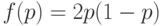 в соответствии с (12) получаем несмещенную оценку
в соответствии с (12) получаем несмещенную оценку
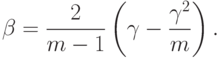 |
( 13) |
Таким образом, можно применять общий метод проверки гипотез о люсианах в асимптотике растущей размерности с
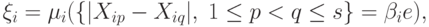
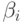 определяются с помощью формулы (13) по
определяются с помощью формулы (13) по  - общему числу единиц, стоящих на
- общему числу единиц, стоящих на  -м месте в люсианах
-м месте в люсианах  , а
, а  - вектор размерности
- вектор размерности 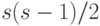 с единичными координатами. Тогда несмещенная оценка 0, о которой идет речь в методе проверки гипотез по совокупности малых выборок, имеет вид
с единичными координатами. Тогда несмещенная оценка 0, о которой идет речь в методе проверки гипотез по совокупности малых выборок, имеет вид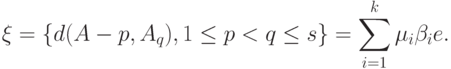
Для использования статистики типа  , распределение которой приближается с помощью нормального распределения
, распределение которой приближается с помощью нормального распределения
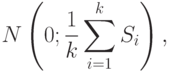
 . Для этого достаточно найти математические ожидания элементов матрицы
. Для этого достаточно найти математические ожидания элементов матрицы 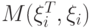 как функции (многочлены) от
как функции (многочлены) от 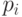 , а затем использовать формулу (12) для получения несмещенных оценок.
, а затем использовать формулу (12) для получения несмещенных оценок.Вычисление матрицы 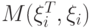 хотя и трудоемко, но не содержит каких-либо принципиальных трудностей. В [
[
5.13
]
] вычислены диагональные элементы рассматриваемой матрицы. Вычисление занимает около 2,5 страниц (с.299-301), Поэтому здесь приведен только окончательный итог.
хотя и трудоемко, но не содержит каких-либо принципиальных трудностей. В [
[
5.13
]
] вычислены диагональные элементы рассматриваемой матрицы. Вычисление занимает около 2,5 страниц (с.299-301), Поэтому здесь приведен только окончательный итог.
Обозначим для краткости 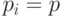 . В [
[
5.13
]
] показано, что
. В [
[
5.13
]
] показано, что
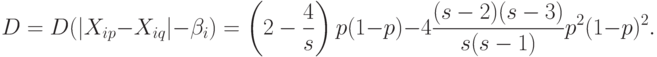
Если двухэлементные множества 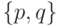 и
и 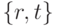 не имеют ни одного общего элемента, то
не имеют ни одного общего элемента, то
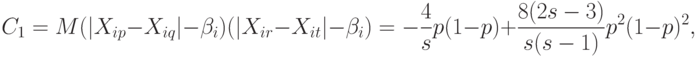
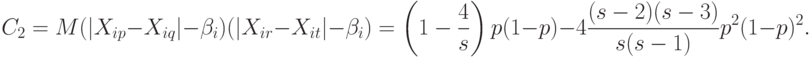
С помощью формулы (12) получаем несмещенные оценки для  и
и 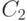 как многочленов от
как многочленов от  :
:

С помощью трех чисел 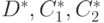 выписывается несмещенная оценка матрицы ковариаций вектора
выписывается несмещенная оценка матрицы ковариаций вектора 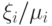 , которую обозначим
, которую обозначим  . Тогда асимптотически нормальный вектор
. Тогда асимптотически нормальный вектор  имеет нулевое математическое ожидание и ковариационную матрицу, несмещенно и состоятельно (в смысле соотношений (7)) оцениваемую с помощью
имеет нулевое математическое ожидание и ковариационную матрицу, несмещенно и состоятельно (в смысле соотношений (7)) оцениваемую с помощью
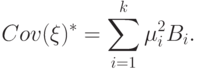 |
( 14) |
Асимптотическая нормальность доказывается, естественно, в схеме серий. Достаточным условием является существование положительной константы  такой, что
такой, что
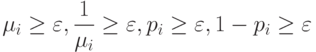 |
( 15) |
 и
и 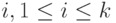 .
.Поскольку  и
и 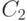 являются многочленами четвертой степени от
являются многочленами четвертой степени от  , то несмещенные оценки для них существуют при
, то несмещенные оценки для них существуют при  . Если же
. Если же  , то несмещенных оценок не существует. Поэтому указанным методом проверять согласованность можно лишь при числе люсианов
, то несмещенных оценок не существует. Поэтому указанным методом проверять согласованность можно лишь при числе люсианов  .
.
