|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистика временных рядов
Под временными рядами понимают детерминированные или случайные функции от времени. При этом время предполагается дискретным, в противном случае говорят о случайных процессах, а не о временных рядах.
10.1. Методы анализа и прогнозирования временных рядов
Модели стационарных и нестационарных временных рядов. Пусть 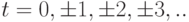 .. Рассмотрим временной ряд
.. Рассмотрим временной ряд 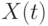 . Пусть сначала временной ряд принимает числовые значения. Это могут быть, например, цены на батон хлеба в соседнем магазине или курс обмена доллара на рубли в ближайшем обменном пункте. Обычно в поведении временного ряда выявляют две основные тенденции - тренд и периодические колебания.
. Пусть сначала временной ряд принимает числовые значения. Это могут быть, например, цены на батон хлеба в соседнем магазине или курс обмена доллара на рубли в ближайшем обменном пункте. Обычно в поведении временного ряда выявляют две основные тенденции - тренд и периодические колебания.
При этом под трендом понимают зависимость от времени линейного, квадратичного или иного типа, которую выявляют тем или иным способом сглаживания (например, экспоненциального сглаживания) либо расчетным путем, в частности, с помощью метода наименьших квадратов. Другими словами, тренд - это очищенная от случайностей основная тенденция временного ряда.
Временной ряд обычно колеблется вокруг тренда, причем отклонения от тренда часто обнаруживают правильность. Часто это связано с естественной или назначенной периодичностью, например, сезонной или недельной, месячной или квартальной (например, в соответствии с графиками выплаты заработной платы и уплаты налогов). Иногда наличие периодичности и тем более ее причины неясны, и задача статистика - выяснить, действительно ли имеется периодичность.
Элементарные методы оценки характеристик временных рядов обычно достаточно подробно рассматриваются в курсах "Общей теории статистики" (см., например, учебники [ [ 10.3 ] , [ 10.18 ] ]), поэтому нет необходимости подробно разбирать их здесь. О некоторых современных методах оценивания длины периода и самой периодической составляющей речь пойдет ниже в 10.2.
Характеристики временных рядов. Для более подробного изучения временных рядов используются вероятностно-статистические модели. При этом временной ряд 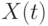 рассматривается как случайный процесс (с дискретным временем). Основными характеристиками
рассматривается как случайный процесс (с дискретным временем). Основными характеристиками 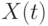 являются математическое ожидание
являются математическое ожидание 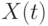 , т.е.
, т.е.
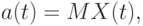
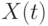 , т.е.
, т.е.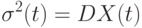
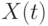
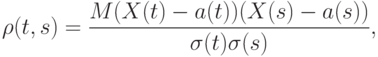
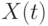 и
и 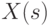 .
.В теоретических и прикладных исследованиях рассматривают широкий спектр моделей временных рядов. Выделим сначала стационарные модели. В них совместные функции распределения 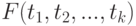 для любого числа моментов времени
для любого числа моментов времени  , а потому и все перечисленные выше характеристики временного ряда не меняются со временем. В частности, математическое ожидание и дисперсия являются постоянными величинами, автокорреляционная функция зависит только от разности
, а потому и все перечисленные выше характеристики временного ряда не меняются со временем. В частности, математическое ожидание и дисперсия являются постоянными величинами, автокорреляционная функция зависит только от разности 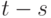 . Временные ряды, не являющиеся стационарными, называются нестационарными.
. Временные ряды, не являющиеся стационарными, называются нестационарными.
Линейные регрессионные модели с гомоскедастичными и гетероскедастичными, независимыми и автокоррелированными остатками. Как видно из сказанного выше, основное - это "очистка" временного ряда от случайных отклонений, т.е. оценивание математического ожидания. В отличие от простейших моделей регрессионного анализа, рассмотренных в "Многомерный статистический анализ" , здесь естественным образом появляются более сложные модели. Например, дисперсия может зависеть от времени. Такие модели называют гетероскедастичными, а те, в которых нет зависимости от времени - гомоскедастичными. (Точнее говоря, эти термины могут относиться не только к переменной "время", но и к другим переменным.)
Далее в "Многомерный статистический анализ" предполагалось, что погрешности независимы между собой. В терминах настоящей лекции это означало бы, что автокорреляционная функция должна быть вырожденной - равняться 1 при равенстве аргументов и 0 при их неравенстве. Ясно, что для реальных временных рядов так бывает отнюдь не всегда. Если естественный ход изменений наблюдаемого процесса является достаточно быстрым по сравнению с интервалом между последовательными наблюдениями, то можно ожидать "затухания" автокорреляции и получения практически независимых остатков, в противном случае остатки будут автокоррелированы.
Идентификация моделей. Под идентификацией моделей обычно понимают выявление их структуры и оценивание параметров. Поскольку структура - это тоже параметр, хотя и нечисловой, то речь идет об одной из типовых задач прикладной статистики - оценивании параметров.
Проще всего задача оценивания решается для линейных (по параметрам) моделей с гомоскедастичными независимыми остатками. Восстановление зависимостей во временных рядах может быть проведено на основе методов наименьших квадратов и наименьших модулей оценивания параметров в моделях линейной (по параметрам) регрессии. На случай временных рядов переносятся результаты, связанные с оцениванием необходимого набора регрессоров, в частности, легко получить предельное геометрическое распределение оценки степени тригонометрического полинома.
Однако на более общую ситуацию такого простого переноса сделать нельзя. Так, например, в случае временного ряда с гетероскедастичными и автокоррелированными остатками снова можно воспользоваться общим подходом метода наименьших квадратов, однако система уравнений метода наименьших квадратов и, естественно, ее решение будут иными. Формулы в терминах матричной алгебры, о которых упоминалось в "Многомерный статистический анализ" , будут отличаться. Поэтому рассматриваемый метод называется " обобщенный метод наименьших квадратов (ОМНК)".
Замечание. Как уже отмечалось в "Многомерный статистический анализ" , простейшая модель метода наименьших квадратов допускает весьма далекие обобщения, особенно в области систем одновременных эконометрических уравнений для временных рядов. Для понимания соответствующей теории и алгоритмов необходимо владение методами матричной алгебры. Поэтому мы отсылаем тех, кому это интересно, к литературе по системам эконометрических уравнений [ [ 10.2 ] , [ 10.15 ] ] и непосредственно по временным рядам [ [ 2.6 ] , [ 10.8 ] ], в которой большое внимание уделено спектральной теории, т.е. выделению сигнала из шума и разложению его на гармоники. Подчеркнем еще раз, что за каждой лекцией настоящей книги стоит большая область научных и прикладных исследований, изучению которой следовало бы уделить больше времени и места. Однако из-за ограниченности объема книги мы вынуждены сделать изложение конспективным.
Системы эконометрических уравнений. В качестве первоначального примера рассмотрим эконометрическую модель временного ряда, описывающего рост индекса потребительских цен (индекса инфляции). Пусть 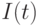 - рост цен в месяц
- рост цен в месяц  (подробнее об этой проблематике см. гл.7 в [
[
2.15
]
]). По мнению некоторых экономистов естественно предположить, что
(подробнее об этой проблематике см. гл.7 в [
[
2.15
]
]). По мнению некоторых экономистов естественно предположить, что
 |
( 1) |
 - рост цен в предыдущий месяц (а
- рост цен в предыдущий месяц (а  - некоторый коэффициент затухания, предполагающий, что при отсутствии внешних воздействий рост цен прекратится),
- некоторый коэффициент затухания, предполагающий, что при отсутствии внешних воздействий рост цен прекратится),  - константа (она соответствует линейному изменению величины
- константа (она соответствует линейному изменению величины 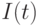 со временем),
со временем), 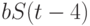 - слагаемое, соответствующее влиянию эмиссии денег (т.е. увеличения объема денег в экономике страны, осуществленному Центральным банком) в размере
- слагаемое, соответствующее влиянию эмиссии денег (т.е. увеличения объема денег в экономике страны, осуществленному Центральным банком) в размере 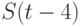 и пропорциональное эмиссии с коэффициентом
и пропорциональное эмиссии с коэффициентом  , причем это влияние проявляется не сразу, а через 4 месяца; наконец,
, причем это влияние проявляется не сразу, а через 4 месяца; наконец,  - это неизбежная погрешность.
- это неизбежная погрешность.Модель (1), несмотря на свою простоту, демонстрирует многие характерные черты гораздо более сложных эконометрических моделей. Во-первых, обратим внимание на то, что некоторые переменные, такие как 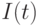 , определяются (рассчитываются) внутри модели. Их называют эндогенными ( внутренними ). Другие задаются извне (это экзогенные переменные). Иногда, как в теории управления, среди экзогенных переменных, выделяют управляемые переменные - те, с помощью выбора значений которых можно привести систему в нужное состояние.
, определяются (рассчитываются) внутри модели. Их называют эндогенными ( внутренними ). Другие задаются извне (это экзогенные переменные). Иногда, как в теории управления, среди экзогенных переменных, выделяют управляемые переменные - те, с помощью выбора значений которых можно привести систему в нужное состояние.
Во-вторых, в соотношении (1) появляются переменные новых типов - с лагами, т.е. аргументы в переменных относятся не к текущему моменту времени, а к некоторым прошлым моментам.
В-третьих, составление эконометрической модели типа (1) - это отнюдь не рутинная операция. Например, запаздывание именно на 4 месяца в связанном с эмиссией денег слагаемом 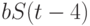 - это результат достаточно изощренной предварительной статистической обработки. Далее, требует изучения вопрос зависимости или независимости величин
- это результат достаточно изощренной предварительной статистической обработки. Далее, требует изучения вопрос зависимости или независимости величин 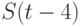 и
и 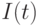 в различные моменты времени
в различные моменты времени  . От решения этого вопроса зависит, как уже отмечалось выше, конкретная реализация процедуры метода наименьших квадратов.
. От решения этого вопроса зависит, как уже отмечалось выше, конкретная реализация процедуры метода наименьших квадратов.
С другой стороны, в модели (1) всего 3 неизвестных параметра, и постановку метода наименьших квадратов сформулировать нетрудно:
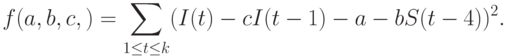
Проблема идентифицируемости. Представим теперь модель типа (1) с большим числом эндогенных и экзогенных переменных, с лагами и сложной внутренней структурой. Вообще говоря, ниоткуда не следует, что существует хотя бы одно решение у такой системы. Поэтому возникает не одна, а две проблемы. Имеется ли хотя одно решение (проблема идентифицируемости)? Если да, то как найти наилучшее решение из возможных? (Это - проблема статистической оценки параметров.)
И первая, и вторая задачи достаточно сложны. Для решения обеих задач разработано множество методов, обычно достаточно сложных, лишь часть из которых имеет научное обоснование. В частности, достаточно часто пользуются статистическими оценками, не являющимися состоятельными (строго говоря, их даже нельзя назвать оценками).
Коротко опишем некоторые распространенные приемы при работе с системами линейных эконометрических уравнений.
Система линейных одновременных эконометрических уравнений. Чисто формально можно все переменные выразить через переменные, зависящие только от текущего момента времени. Например, в случае уравнения (1) достаточно положить
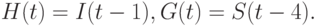
Тогда уравнение примет вид
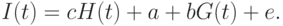 |
( 2) |
Отметим здесь же возможность использования регрессионных моделей с переменной структурой путем введения фиктивных переменных. Эти переменные при одних значениях времени (скажем, начальных) принимают заметные значения, а при других - сходят на нет (становятся фактически равными 0). В результате формально (математически) одна и та же модель описывает совсем разные зависимости.
Косвенный, двухшаговый и трехшаговый методы наименьших квадратов. Как уже отмечалось, разработана масса методов эвристического анализа систем эконометрических уравнений. Они предназначены для решения тех или иных проблем, возникающих при попытках найти численные решения систем уравнений.
Одна из проблем связана с наличием априорных ограничений на оцениваемые параметры. Например, доход домохозяйства может быть потрачен либо на потребление, либо на сбережение. Значит, сумма долей этих двух видов трат априори равна 1. А в системе эконометрических уравнений эти доли могут участвовать независимо. Возникает мысль оценить их методом наименьших квадратов, не обращая внимания на априорное ограничение, а потом подкорректировать. Такой подход называют косвенным методом наименьших квадратов.
Двухшаговый метод наименьших квадратов состоит в том, что оценивают параметры отдельного уравнения системы, а не рассматривают систему в целом. В то же время трехшаговый метод наименьших квадратов применяется для оценки параметров системы одновременных уравнений в целом. Сначала к каждому уравнению применяется двухшаговый метод с целью оценить коэффициенты и погрешности каждого уравнения, а затем построить оценку для ковариационной матрицы погрешностей. После этого для оценивания коэффициентов всей системы применяется обобщенный метод наименьших квадратов.
Менеджеру и экономисту не следует становиться специалистом по составлению и решению систем эконометрических уравнений, даже с помощью тех или иных программных систем, но он должен быть осведомлен о возможностях этого направления эконометрики, чтобы в случае производственной необходимости квалифицированно сформулировать задание для специалистов по прикладной статистике.
От оценивания тренда (основной тенденции) перейдем ко второй основной задаче эконометрики временных рядов - оцениванию периода (цикла).
