|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Многомерный статистический анализ
Контрольные вопросы и задачи
- Имеются данные за несколько лет о торговом обороте
 западно-германского предприятия и его расходах на рекламу
западно-германского предприятия и его расходах на рекламу  . Данные представлены в табл.9.4.
. Данные представлены в табл.9.4.Таблица 9.4. Расходы на рекламу и торговый оборот предприятия Годы, 
1968 1969 1970 1971 1972 1973 1974 1975 Расходы на рекламу 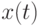 , тыс. марок
, тыс. марок4 4 5 6 8 8 10 11 Торговый оборот 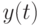 , млн.марок
, млн.марок4 5 6 6 8 10 12 13 Вычислите линейный коэффициент корреляции между случайными величинами
 и
и  . С помощью метода наименьших квадратов определите коэффициенты линейной регрессии
. С помощью метода наименьших квадратов определите коэффициенты линейной регрессии 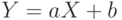 . Постройте график (заданные точки
. Постройте график (заданные точки 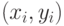 и прямую
и прямую 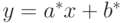 ). Найдите доверительные границы для регрессионной зависимости (при доверительной вероятности
). Найдите доверительные границы для регрессионной зависимости (при доверительной вероятности  ). Нанесите доверительные границы на график. Сделайте точечный и интервальный прогноз для торгового оборота при расходах на рекламу, равных 15 тыс. марок ФРГ.
). Нанесите доверительные границы на график. Сделайте точечный и интервальный прогноз для торгового оборота при расходах на рекламу, равных 15 тыс. марок ФРГ.Аналогичным образом изучите зависимости расходов на рекламу
 и торгового оборота
и торгового оборота  от времени
от времени  (за начало отсчета целесообразно взять 1971 год). Какой смысл имеет в этих случаях коэффициент корреляции?
(за начало отсчета целесообразно взять 1971 год). Какой смысл имеет в этих случаях коэффициент корреляции? - Семь школьников выполняют несколько заданий по математике и физике, которые оцениваются баллами 1-5, затем вычисляется средний балл для каждого школьника по каждому предмету: по математике -
 , по физике -
, по физике - 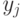 . Данные представлены в табл.9.5. Определите, существует ли корреляция (т.е. связь) между этими оценками, вычислив коэффициент ранговой корреляции Спирмена.
. Данные представлены в табл.9.5. Определите, существует ли корреляция (т.е. связь) между этими оценками, вычислив коэффициент ранговой корреляции Спирмена.
- Исходные данные (табл.9.6) - набор
 пар чисел
пар чисел  , где
, где  - независимая переменная (например, время), а
- независимая переменная (например, время), а  - зависимая (например, индекс инфляции). Предполагается, что переменные связаны зависимостьюгде
- зависимая (например, индекс инфляции). Предполагается, что переменные связаны зависимостьюгде
 и
и  - параметры, неизвестные статистику и подлежащие оцениванию, а
- параметры, неизвестные статистику и подлежащие оцениванию, а  - погрешности, искажающие зависимость.
- погрешности, искажающие зависимость.Таблица 9.6. Исходные данные для расчетов по методу наименьших квадратов 
1 3 4 7 9 10 
12 20 20 32 35 42 Методом наименьших квадратов оцените параметры
 и
и  линейной зависимости. Выпишите восстановленную зависимость.
линейной зависимости. Выпишите восстановленную зависимость.Вычислите восстановленные значения зависимой переменной, сравните их с исходными значениями (найдите разности) и проверьте условие точности вычислений (при отсутствии ошибок в вычислениях сумма исходных значений должна равняться сумме восстановленных).
Найдите остаточную сумму квадратов и оцените дисперсию погрешностей.
Выпишите точечный прогноз, а также верхнюю и нижнюю доверительные границы для него (для доверительной вероятности 0,95).
Рассчитайте прогнозное значение и доверительные границы для него для момента
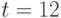 .
.Как изменятся результаты, если доверительная вероятность будет увеличена? А если она будет уменьшена?
- Как в методе наименьших квадратов используются преобразования переменных?
- Как соотносятся задачи группировки и задачи кластер-анализа?
- В табл.9.7 приведены попарные расстояния между десятью социально-психологическими признаками способных к математике школьников [
[
9.10
]
]. Примените к этим данным алгоритмы ближнего соседа, средней связи и дальнего соседа. Для каждого из трех алгоритмов выделите наиболее устойчивые разбиения на кластеры.
Таблица 9.7. Попарные расстояния между социально-психологическими признаками 1 2 3 4 5 6 7 9 10 2 1028 3 1028 608 4 1050 688 610 5 1012 686 636 634 6 1006 566 538 616 562 7 1012 1026 748 692 774 732 8 960 1088 1144 1122 1120 1130 1110 9 1026 878 874 830 836 802 904 1040 10 990 744 674 744 718 580 814 1090 830 - Расскажите о динамике индекса инфляции в России.
Темы докладов, рефератов, исследовательских работ
- Примеры практического использования методов многомерного статистического анализа.
- Для непараметрической модели метода наименьших квадратов в случае линейной функции одной переменной разработайте алгоритмы
- расчета доверительных границ для коэффициентов модели;
- проверки гипотез относительно этих коэффициентов.
- Докажите, что сумма исходных значений зависимой переменной должна быть равна сумме восстановленных значений.
- Критерии качества регрессионной модели.
- Использование непараметрических оценок плотности для восстановления зависимости.
- Теоремы умножения и сложения для индекса инфляции.
- Экспериментальная работа: соберите данные о ценах и рассчитайте индекс инфляции для своего региона (данные о потребительской корзине ИВСТЭ и ценах на базовый момент времени приведены в [ [ 2.15 ] ]).
- Учет инфляции при проведении анализа финансово-хозяйственной деятельности предприятия.

