НОУ ИНТУИТ | Прикладная статистика. Лекция 9: Многомерный статистический анализ

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Доступ: свободный | Студентов: 4093 / 1040 | Оценка: 4.66 / 4.45 | Длительность: 54:13:00

Темы: Математика, Экономика

Специальности: Экономист

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать курс

| Скачать электронную книгу

9.2. Восстановление линейной зависимости между двумя переменными

Начнем с задачи точечного и доверительного оценивания линейной функции одной переменной.

Исходные данные - набор пар чисел (t_k , x_k), k = 1,2,...,n , где t_k - независимая переменная (например, время), а x_k - зависимая (например, индекс инфляции, курс доллара США, объем месячного производства или размер дневной выручки торговой точки). Предполагается, что переменные связаны зависимостью

$x_k=a(t_k-t_{cp})+b+e_k, k=1,2,...,n,$

где

и

- параметры, неизвестные статистику и подлежащие оцениванию, а e_k

- погрешности, искажающие зависимость. Среднее арифметическое моментов времени

$t_{cp}=(t_1+t_2+...+t_n)/n$

введено в модель для облегчения дальнейших выкладок.

Обычно оценивают параметры и линейной зависимости методом наименьших квадратов. Затем восстановленную зависимость используют, например, для точечного и интервального прогнозирования.

Как известно, метод наименьших квадратов был разработан великим немецким математиком К. Гауссом в 1794 г. Согласно этому методу для расчета наилучшей функции, приближающей линейным образом зависимость от , следует рассмотреть функцию двух переменных

$f(x,b)=\sum_{i=1}^n(x_i-a(t_i-t_{cp})-b)^2.$

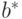Оценки метода наименьших квадратов - это такие значения a^* и b^* , при которых функция f(a,b) достигает минимума по всем значениям аргументов.

Чтобы найти эти оценки, надо вычислить частные производные от функции f(a,b) по аргументам и , приравнять их 0, затем из полученных уравнений найти оценки. Имеем:

$\begin{gathered} \frac{\partial f(a,b)}{\partial a}=\sum_{i=1}^n 2(x_i-a(t_i-t_{cp})-b)(-(t_i-t_{cp})), \\ \frac{\partial f(a,b)}{\partial b}=\sum_{i=1}^n 2(x_i-a(t_i-t_{cp})-b)(-1). \end{gathered}$

Преобразуем правые части полученных соотношений. Вынесем за знак суммы общие множители 2 и (-1). Затем рассмотрим слагаемые. Раскроем скобки в первом выражении, получим, что каждое слагаемое разбивается на три. Во втором выражении также каждое слагаемое есть сумма трех. Значит, каждая из сумм разбивается на три суммы. Имеем:

$\begin{gathered} \frac{\partial f(a,b)}{\partial a}=(-2)(\sum_{i=1}^n x_i(t_i-t_{cp}) -a\sum_{i=1}^n(t_i-t_{cp})^2-b\sum_{i=1}^n(t_i-t_{cp})), \\ \frac{\partial f(a,b)}{\partial b}=(-2)(\sum_{i=1}^n x_i -a\sum_{i=1}^n(t_i-t_{cp})-bn). \end{gathered}$

Приравняем частные производные 0. Тогда в полученных уравнениях можно сократить множитель (-2). Поскольку

$\sum_{i=1}^n(t_i-t_{cp})=0,$

( 1)

уравнения приобретают вид

$\sum_{i=1}^n x_i(t_i-t_{cp})-a\sum_{i=1}^n (t_i-t_{cp})^2=0,\; \sum_{i=1}^n x_i-bn=0.$

Следовательно, оценки метода наименьших квадратов имеют вид

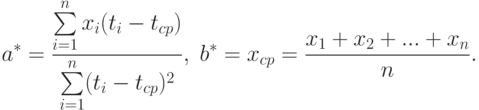$a^*=\frac{\sum\limits_{i=1}^n x_i(t_i-t_{cp})}{\sum\limits_{i=1}^n(t_i-t_{cp})^2},\; b^*=x_{cp}=\frac{x_1+x_2+...+x_n}{n}.$

( 2)

В силу соотношения (1) оценку a^* можно записать в более симметричном виде:

$a^*=\frac{\sum\limits_{i=1}^n(x_i-x_{cp})(t_i-t_{cp})}{\sum\limits_{i=1}^n(t_i-t_{cp})^2}.$

( 3)

Эту оценку нетрудно преобразовать и к виду

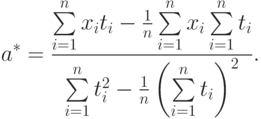$a^*=\frac{\sum\limits_{i=1}^n x_i t_i-\frac{1}{n}\sum\limits_{i=1}^n x_i \sum\limits_{i=1}^n t_i} {\sum\limits_{i=1}^n t_i^2 -\frac{1}{n}\left(\sum\limits_{i=1}^n t_i\right)^2}.$

( 4)

Следовательно, восстановленная функция, с помощью которой можно прогнозировать и интерполировать, имеет вид

$x^*(t)=a^*(t-t_{cp})+b*.$

Обратим внимание на то, что использование t_ср в последней формуле ничуть не ограничивает ее общность. Сравним с моделью вида

Ясно, что

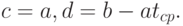
$c=a, d=b-at_{cp}.$

Аналогичным образом связаны оценки параметров:

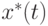Для получения оценок параметров и прогностической формулы нет необходимости обращаться к какой-либо вероятностной модели. Однако для того, чтобы изучать погрешности оценок параметров и восстановленной функции, т.е. строить доверительные интервалы для a^*, b^* и x^*(t) , подобная модель необходима.

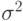Непараметрическая вероятностная модель. Пусть значения независимой переменной t детерминированы, а погрешности e_k, k = 1,2,...,n , - независимые одинаково распределенные случайные величины с нулевым математическим ожиданием и дисперсией $\sigma^2$ неизвестной статистику.

В дальнейшем неоднократно будем использовать Центральную предельную теорему (ЦПТ) теории вероятностей для величин e_k, k = 1,2,...,n (с весами), поэтому для выполнения ее условий необходимо предположить, например, что погрешности , финитны или имеют конечный третий абсолютный момент. Однако заострять внимание на этих внутриматематических "условиях регулярности" нет необходимости.

Асимптотические распределения оценок параметров. Из формулы (2) следует, что

$b^*=\frac{a}{n}\sum_{i=1}^n(t_i-t_{cp})+b+\frac{1}{n}\sum_{i=1}^n e_i= b+\frac{1}{n}\sum_{i=1}^n e_i.$

( 5)

Согласно ЦПТ оценка 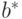b^* имеет асимптотически нормальное распределение с математическим ожиданием и дисперсией $\sigma^2/n$ оценка которой приводится ниже.

Из формул (2) и (5) вытекает, что

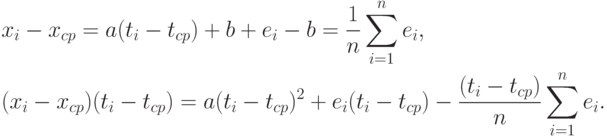
$\begin{aligned} &x_i-x_{cp}=a(t_i-t_{cp})+b+e_i-b=\frac{1}{n}\sum_{i=1}^n e_i, \\ &(x_i-x_{cp})(t_i-t_{cp})=a(t_i-t_{cp})^2+e_i(t_i-t_{cp})-\frac{(t_i-t_{cp})}{n}\sum_{i=1}^n e_i. \end{aligned}$

Последнее слагаемое во втором соотношении при суммировании по i обращается в 0, поэтому из формул (2-4) следует, что

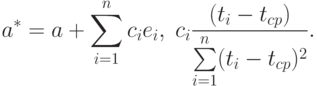$a^*=a+\sum_{i=1}^n c_i e_i,\; c_i\frac{(t_i-t_{cp})}{\sum\limits_{i=1}^n(t_i-t_{cp})^2}.$

( 6)

Формула (6) показывает, что оценка a^* является асимптотически нормальной с математическим ожиданием и дисперсией

$D(a^*)=\sum_{i=1}^n c_i^2 D(e_i)=\frac{\sigma^2}{\sum\limits_{i=1}^n(t_i-t_{cp})^2}.$

Отметим, что многомерная нормальность имеет место, когда каждое слагаемое в формуле (6) мало сравнительно со всей суммой, т.е.

$\lim_{n\rightarrow\infty}\max_{1\le i\le n}|t_i-t_{cp}|/ \left\{ \sum_{i=1}^n(t_i-t_{cp})^2 \right\}^{1/2}.$

Из формул (5) и (6) и исходных предположений о погрешностях вытекает также несмещенность оценок параметров.

Несмещенность и асимптотическая нормальность оценок метода наименьших квадратов позволяют легко указывать для них асимптотические доверительные границы (аналогично границам в "Статистический анализ числовых величин" ) и проверять статистические гипотезы, например, о равенстве определенным значениям, прежде всего 0. Предоставляем читателю возможность выписать формулы для расчета доверительных границ и сформулировать правила проверки упомянутых гипотез.

Асимптотическое распределение прогностической функции. Из формул (5) и (6) следует, что

$M(x^*(t))=M\{a^*(t-t_{cp})+b^*\}=M(a^*)(t-t_{cp})+M(b^*)=a(t-t_{cp})+b=x(t),$

т.е. рассматриваемая оценка прогностической функции является несмещенной. Поэтому

$D(x^*(t))=D(a^*)(t-t_{cp})^2+2M\{(a^*-a)(b^*-b)(t-t_{cp})\}+D(b^*).$

При этом, поскольку погрешности независимы в совокупности и 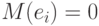M(e_i)=0 , то

$M\{(a^*-a)(b^*-b)(t-t_{cp})\}=frac{1}{n}\sum_{i=1}^n c_i(t-t_{cp})M(e_i^2)= \frac{1}{n}(t-t_{cp})\sigma^2\sum_{i=1}^n c_i=0.$

Таким образом,

$D(x^*(t))=\sigma^2 \left\{ \frac{1}{n}+\frac{(t-t_{cp})^2}{\sum\limits_{i=1}^n(t_i-t_{cp})^2} \right\}.$

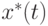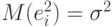Итак, оценка x^*(t) является несмещенной и асимптотически нормальной. Для ее практического использования необходимо уметь оценивать остаточную дисперсию $M(e_i^2)=\sigma^2$ .

Дальше >>

Авторизоваться

Прикладная статистика

Многомерный статистический анализ

9.2. Восстановление линейной зависимости между двумя переменными

Вопросы и ответы