Многомерный статистический анализ

9.4. Основы теории классификации

При внедрении современных статистических методов в практику фундаментальных и прикладных научно-технических, социально-экономических, медицинских и иных исследований, при разработке соответствующих программных продуктов невозможно обойтись без классификации самих этих методов. Естественно исходить из вида обрабатываемых данных. В соответствии с современными воззрениями делим прикладную статистику на четыре области: - статистика случайных величин (одномерная статистика); многомерный статистический анализ; статистика временных рядов и случайных величин; статистика объектов нечисловой природы. В первой области элемент выборки - число, во второй - вектор, в третьей - функция, в четвертой - объект нечисловой природы.

Как известно, математический аппарат статистики объектов нечисловой природы базируется на использовании расстояний (мер близости, показателей различия) в пространствах таких объектов. Это вызвано отсутствием в таких пространствах операций суммирования, на которых основано большинство методов других областей статистики. Любые методы, использующие только расстояния (меры близости, показатели различия) между объектами, следует относить к статистике объектов нечисловой природы, поскольку такие методы могут работать с объектами произвольного пространства, если в нем задана метрика или ее аналоги. Таким образом, весьма многие методы прикладной статистики следует включать в статистику объектов нечисловой природы.

В настоящем параграфе рассматривается важное направление прикладной статистики - математические методы классификации. Значительную их часть следовало бы отнести к статистике объектов нечисловой природы, а именно, методы классификации, основанные на расстояниях между объектами. Однако исторически теория классификации рассматривается в основном в рамках многомерного статистического анализа, поскольку многие ее методы используют специфику конечномерного евклидова пространства.

Основные направления в математической теории классификации. Какие научные исследования относить к этой теории? Исходя из потребностей специалиста, применяющего математические методы классификации, целесообразно принять, что сюда входят исследования, во-первых, отнесенные самими авторами к этой теории; во вторых, связанные с ней общностью тематики, хотя бы их авторы и не упоминали термин "классификация". Это предполагает ее сложную внутреннюю структуру.

В литературных источниках наряду с "классификацией" используются близкие по смыслу термины: "группировка", "распознавание образов", "диагностика", "дискриминация", "сортировка" и др. Терминологический разнобой связан прежде всего с традициями научных кланов, к которым относятся авторы публикаций, а также с внутренним делением самой теории классификации.

В научных исследованиях по современной теории классификации можно выделить два относительно самостоятельных направления. Одно из них опирается на опыт таких наук, как биология, география, геология, и таких прикладных областей, как ведение классификаторов продукции и библиотечное дело. Типичные объекты рассмотрения - классификация химических элементов (таблица Д.И. Менделеева), биологическая систематика, универсальная десятичная классификация публикаций (УДК), классификатор товаров на основе штрих-кодов.

Другое направление опирается на опыт технических исследований, экономики, маркетинговых исследований, социологии, медицины. Типичные задачи - техническая и медицинская диагностика, а также, например, разбиение на группы отраслей промышленности, тесно связанных между собой, выделение групп однородной продукции. Обычно используются такие термины, как "распознавание образов" или "дискриминантный анализ". Это направление обычно опирается на математические модели; для проведения расчетов интенсивно используется ЭВМ. Однако относить его к математике столь же нецелесообразно, как астрономию или квантовую механику. Рассматриваемые математические модели можно и нужно изучать на формальном уровне, и такие исследования проводятся. Но направление в целом сконцентрировано на решении конкретных задач прикладных областей и вносит вклад в технические или экономические науки, медицину, социологию, но, как правило, не в математику. Использование математических методов как инструмента исследования нельзя относить к чистой математике.

В 60-х годах XX века внутри прикладной статистики достаточно четко оформилась область, посвященная методам классификации. Несколько модифицируя формулировки М. Дж. Кендалла и А. Стьюарта 1966 г. (см. русский перевод [ [ 9.4 ] , с.437]), в теории классификации выделим три подобласти: дискриминация (дискриминантный анализ), кластеризация (кластер-анализ), группировка. Опишем эти подобласти.

В дискриминантном анализе классы предполагаются заданными - плотностями вероятностей или обучающими выборками. Задача состоит в том, чтобы вновь поступающий объект отнести в один из этих классов. У понятия "дискриминация" имеется много синонимов: диагностика, распознавание образов с учителем, автоматическая классификация с учителем, статистическая классификация и т.д.

При кластеризации и группировке целью является выявление и выделение классов. Синонимы: построение классификации, распознавание образов без учителя, автоматическая классификация без учителя, типология, таксономия и др. Задача кластер-анализа состоит в выяснении по эмпирическим данным, насколько элементы "группируются" или распадаются на изолированные "скопления", "кластеры" (от англ. cluster - гроздь, скопление). Иными словами, - выявление естественного разбиения на классы, свободного от субъективизма исследователя, а цель - выделение групп однородных объектов, сходных между собой, при резком отличии этих групп друг от друга.

При группировке, наоборот, "мы хотим разбить элементы на группы независимо от того, естественны ли границы разбиения или нет" [ [ 9.4 ] , с.437]. Цель по-прежнему состоит в выявлении групп однородных объектов, сходных между собой (как в кластер-анализе), однако "соседние" группы могут не иметь резких различий (в отличие от кластер-анализа). Границы между группами условны, не являются естественными, зависят от субъективизма исследователя. Аналогично при лесоустройстве проведение просек (границ участков) зависит от специалистов лесного ведомства, а не от свойств леса.

Задачи кластеризации и группировки принципиально различны, хотя для их решения могут применяться одни и те же алгоритмы. Важная для практической деятельности проблема состоит в том, чтобы понять, разрешима ли задача кластер-анализа для конкретных данных или возможна только их группировка, поскольку совокупность объектов достаточно однородна и не разбивается на резко разделяющиеся между собой кластеры.

Как правило, в математических задачах кластеризации и группировки основное - выбор метрики, расстояния между объектами, меры близости, сходства, различия. Хорошо известно, что для любого заданного разбиения объектов на группы и любого 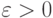можно указать метрику такую, что расстояния между объектами из одной группы будут меньше , а между объектами из разных групп - больше 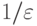. Тогда любой разумный алгоритм кластеризации, использующий эту метрику, даст именно заданное разбиение.

Понимание и обсуждение постановок задач осложняется использованием одного и того же термина в разных смыслах. Термином "классификация" (и термином "диагностика") обозначают, по крайней мере, три разные вещи: процедуру построения классификации (и выделение классов, используемых при диагностике), построенную классификацию (систему выделенных классов) и процедуру ее использования (правила отнесения вновь поступающего объекта к одному из ранее выделенных классов). Другими словами, имеем естественную триаду: построение - изучение - использование классификации.

Как уже отмечалось, для построения системы диагностических классов используют разнообразные методы кластерного анализа и группировки объектов. Наименее известен второй член триады (отсутствующий у Кендалла и Стьюарта [ [ 9.4 ] ]) - изучение отношений эквивалентности, полученных в результате построения системы диагностических классов. Статистический анализ полученных, в частности экспертами, отношений эквивалентности - часть статистики бинарных отношений и тем самым - статистики объектов нечисловой природы (см. "Статистика нечисловых данных" ).

Диагностика в узком смысле слова (процедура использования классификации, т.е. отнесения вновь поступающего объекта к одному из выделенных ранее классов) - предмет дискриминантного анализа. Отметим, что с точки зрения статистики объектов нечисловой природы дискриминантный анализ является частным случаем общей схемы регрессионного анализа, соответствующим ситуации, когда зависимая переменная принимает конечное число значений, а именно - номера классов, а вместо квадрата разности стоит функция потерь от неправильной классификации. Однако есть ряд специфических постановок, выделяющих задачи диагностики среди всех регрессионных задач.

О построении диагностических правил. Начнем с краткого обсуждения одного распространенного заблуждения. Иногда рекомендуют сначала построить систему диагностических классов, а потом в каждом диагностическом классе отдельно проводить регрессионный анализ (в классическом смысле) или применять иные методы многомерного статистического анализа. Однако обычно забывают, что при этом нельзя опираться на вероятностную модель многомерного нормального распределения, так как распределение результатов наблюдений, попавших в определенный кластер, будет отнюдь не нормальным, а усеченным нормальным (усечение определяется границами кластера).

Процедуры построения диагностических правил делятся на вероятностные и детерминированные. К первым относятся так называемые задачи расщепления смесей. В них предполагается, что распределение вновь поступающего случайного элемента является смесью вероятностных законов, соответствующих диагностическим классам. Как и при выборе степени полинома в регрессии (см. 9.3), при анализе реальных социально-экономических данных встает вопрос об оценке числа элементов смеси, т.е. числа диагностических классов. Были изучены результаты применения обычно рекомендуемого критерия Уилкса для оценки числа элементов смеси. Оказалось (см. статью [ [ 9.13 ] ]), что оценка с помощью критерия Уилкса не является состоятельной, асимптотическое распределение этой оценки - геометрическое, как и в случае задачи восстановления зависимости в регрессионном анализе. Итак, продемонстрирована несостоятельность обычно используемых оценок. Для получения состоятельных оценок достаточно связать уровень значимости в критерии Уилкса с объемом выборки, как это было предложено и для задач регрессии [ [ 9.11 ] ].

Как уже отмечалось, задачи построения системы диагностических классов целесообразно разбить на два типа: с четко разделенными кластерами (задачи кластер-анализа) и с условными границами, непрерывно переходящими друг в друга классами (задачи группировки). Такое деление полезно, хотя в обоих случаях могут применяться одинаковые алгоритмы. Сколько же существует алгоритмов построения системы диагностических правил? Иногда называют то или иное число. На самом же деле их бесконечно много, в чем нетрудно убедиться.

Действительно, рассмотрим один определенный алгоритм - алгоритм средней связи. Он основан на использовании некоторой меры близости 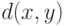между объектами и . Как он работает? На первом шаге каждый объект рассматривается как отдельный кластер. На каждом следующем шаге объединяются два ближайших кластера. Расстояние между объектами рассчитывается как средняя связь (отсюда и название алгоритма), т.е. как среднее арифметическое расстояний между парами объектов, один из которых входит в первый кластер, а другой - во второй. В конце концов все объекты объединяются вместе, и результат работы алгоритма представляет собой дерево последовательных объединений (в терминах теории графов), или "Дендрограмму". Из нее можно выделить кластеры разными способами. Один подход - исходя из заданного числа кластеров. Другой - из соображений предметной области. Третий - исходя из устойчивости (если разбиение долго не менялось при возрастании порога объединения - значит, оно отражает реальность). И т.д.

К алгоритму средней связи естественно сразу добавить алгоритм ближайшего соседа (когда расстоянием между кластерами называется минимальное из расстояний между парами объектов, один из которых входит в первый кластер, а другой - во второй). А также и алгоритм дальнего соседа (когда расстоянием между кластерами называется максимальное из расстояний между парами объектов, один из которых входит в первый кластер, а другой - во второй).

Алгоритм средней связи, как легко проверить, порождает бесконечное (континуальное) семейство алгоритмов кластер-анализа. Дело в том, что величина 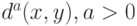, также является мерой близости между и и порождает новый алгоритм. Если параметр пробегает отрезок, то получается бесконечно много алгоритмов классификации.

Каким из них пользоваться при обработке данных? Дело осложняется тем, что практически в любом пространстве данных мер близости различных видов существует весьма много. Именно в связи с обсуждаемой проблемой следует указать на принципиальное различие между кластер-анализом и задачами группировки.

Если классы реальны, естественны, существуют на самом деле, четко отделены друг от друга, то любой алгоритм кластер-анализа их выделит. Следовательно, в качестве критерия естественности классификации следует рассматривать ее устойчивость относительно выбора алгоритма кластер-анализа.

Проверить устойчивость можно, применив к данным несколько подходов, например, столь непохожие алгоритмы, как "ближнего соседа" и "дальнего соседа". Если полученные результаты содержательно близки, то они адекватны действительности. В противном случае следует предположить, что естественной классификации не существует, задача кластер-анализа не имеет решения, и можно проводить только группировку.

Как уже отмечалось, часто применяется так называемый агломеративный иерархический алгоритм "Дендрограмма", в котором вначале все элементы рассматриваются как отдельные кластеры, а затем на каждом шагу объединяются два наиболее близких кластера. Для работы "Дендрограммы" необходимо задать правило вычисления расстояния между кластерами. Оно вычисляется через расстояние 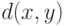между элементами и . 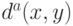Поскольку при 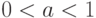также расстояние, то, как правило, существует бесконечно много различных вариантов этого алгоритма. Представим себе, что они применяются для обработки одних и тех же реальных данных. Если при всех получается одинаковое разбиение элементов на кластеры, т.е. результат работы алгоритма устойчив по отношению к изменению (в смысле общей схемы устойчивости, рассмотренной в "Теоретическая база прикладной статистики" ), то имеем "естественную" классификацию. В противном случае результат зависит от субъективно выбранного исследователем параметра , т.е. задача кластер-анализа неразрешима (предполагаем, что выбор нельзя специально обосновать). Задача группировки в этой ситуации имеет много решений. Из них можно выбрать одно по дополнительным критериям.

Следовательно, получаем эвристический критерий: если решение задачи кластер-анализа существует, то оно находится с помощью любого алгоритма. Целесообразно использовать наиболее простой.

Проблема поиска естественной классификации. Существуют различные точки зрения на эту проблему. Естественная классификация обычно противопоставляется искусственной. На Всесоюзной школе-семинаре "Использование математических методов в задачах классификации" (г. Пущино, 1986 г.), в частности, были высказаны мнения, что естественная классификация:

• закон природы;
• основана на глубоких закономерностях, тогда как искусственная классификация - на неглубоких;
• для конкретного индивида та, которая наиболее быстро вытекает из его тезауруса;
• удовлетворяет многим целям; цель искусственной классификации задает человек;
• классификация с точки зрения потребителя продукции;
• классификация, позволяющая делать прогнозы;
• имеет критерием устойчивость.

Приведенные высказывания уже дают представление о больших расхождениях в понимании "естественной классификации". Этот термин следует признать нечетким, как, впрочем, и многие другие термины, и профессиональные - социально-экономические, научно-технические, и используемые в обыденном языке. Нетрудно подробно обосновать нечеткость естественного языка и тот факт, что "мы мыслим нечетко", что, однако, не слишком мешает нам решать производственные и жизненные проблемы. Кажущееся рациональным требование выработать сначала строгие определения, а потом развивать науку - невыполнимо. Следовать ему - значит отвлекать силы от реальных задач. При системном подходе к теории классификации становится ясно, что строгие определения можно надеяться получить на последних этапах построения теории. Мы же сейчас находимся чаще всего на первых этапах. Поэтому, не давая определения понятиям "естественная классификация" и "естественная диагностика", обсудим, как проверить на "естественность" классификацию (набор диагностических классов), полученную расчетным путем.

Можно выделить два критерия "естественности", по поводу которых имеется относительное согласие.

А. Естественная классификация должна быть реальной, соответствующей действительному миру, лишенной внесенного исследователем субъективизма.

Б. Естественная классификация должна быть важной или с научной точки зрения (давать возможность прогноза, предсказания новых свойств, сжатия информации и т.д.), или с практической.

Пусть классификация проводится на основе информации об объектах, представленной в виде матрицы "объект-признак" или матрицы попарных расстояний (мер близости). Пусть алгоритм классификации дал разбиение на кластеры. Как можно получить доводы в пользу естественности этой классификации? Например, уверенность в том, что она - закон природы, может появиться только в результате ее длительного изучения и практического применения. Это соображение относится и к другим из перечисленных выше критериев, в частности к Б (важности). Сосредоточимся на критерии А (реальности).

Понятие "реальности" кластера требует специального обсуждения (оно начато в работе [ [ 9.13 ] ]). Рассмотрим существо различий между понятиями "классификация" и "группировка". Пусть, к примеру, необходимо деревья, растущие в определенной местности, разбить на группы находящихся рядом друг с другом. Ясна интуитивная разница между несколькими отдельными рощами, далеко отстоящими друг от друга и разделенными полями, и сплошным лесом, разбитым просеками на квадраты с целью лесоустройства.

Однако формально определить эту разницу столь же сложно, как определить понятие "куча зерен", чем занимались еще в Древней Греции. Ясно, что одно зерно не составляет кучи, два зерна не составляют кучи,... Если к тому, что не составляет кучи, добавить еще одно зерно, то куча не получится. Значит - по принципу математической индукции - никакое количество зерен не составляет кучи. Но ясно, что миллиард зерен - большая куча зерен - подсчитайте объем!

Переформулируем сказанное в терминах "кластер-анализа" и "методов группировки". Выделенные с помощью первого подхода кластеры реальны, а потому могут рассматриваться как кандидаты в "естественные". Группировка дает "искусственные" классы, которые не могут быть "естественными".

Выборку из унимодального распределения можно, видимо, рассматривать как "естественный", "реальный" кластер. Применим к ней какой-либо алгоритм классификации ("средней связи", "ближайшего соседа" и т.п.). Он даст какое-то разбиение на классы, которые, разумеется, не являются "реальными", поскольку отражают прежде всего свойства алгоритма, а не исходных данных. Как отличить такую ситуацию от противоположной, когда имеются реальные кластеры и алгоритм классификации более или менее точно их выделяет? Как известно, "критерий истины - практика", но слишком много времени необходимо для применения подобного критерия. Поэтому представляет интерес критерий, оценивающий "реальность" выделяемых с помощью алгоритма классификации кластеров одновременно с применением этого алгоритма.

Такой показатель существует - это критерий устойчивости. Устойчивость - понятие широкое. Общая схема формулирования и изучения проблем устойчивости рассмотрена в "Теоретическая база прикладной статистики" . В частности, поскольку значения признаков всегда измеряются с погрешностями, то "реальное" разбиение должно быть устойчиво (т.е. не меняться или меняться слабо) при малых отклонениях исходных данных. Алгоритмов классификации существует бесконечно много, и "реальное" разбиение должно быть устойчиво по отношению к переходу к другому алгоритму. Другими словами, если "реальное" разбиение на классы возможно, то оно находится с помощью любого алгоритма автоматической классификация. Следовательно, критерием естественности классификации может служить совпадение результатов работы двух достаточно различающихся алгоритмов, например "ближайшего соседа" и "дальнего соседа".

Выше рассмотрены два типа "глобальных" критериев "естественности классификации", касающихся разбиения в целом. "Локальные" критерии относятся к отдельным кластерам. Простейшая постановка такова: достаточно ли однородны два кластера (две совокупности) для их объединения? Если объединение возможно, то кластеры не являются "естественными". Преимущество этой постановки в том, что она допускает применение статистических критериев однородности двух выборок. В одномерном случае (классификация по одному признаку) разработано большое число подобных критериев - Крамера-Уэлча, Смирнова, омега-квадрат (Лемана-Розенблатта), Вилкоксона, Ван-дер-Вардена, Лорда, Стьюдента и др. (см. "Статистический анализ числовых величин" и справочник [ [ 2.1 ] ]). Имеются критерии и для многомерных данных. Для одного из видов объектов нечисловой природы - люсианов - статистические методы выделения "реальных" кластеров описаны в работе [ [ 5.15 ] ].

Что касается глобальных критериев, то для изучения устойчивости по отношению к малым отклонениям исходных данных естественно использовать метод статистических испытаний и проводить расчеты по "возмущенным" данным. Некоторые теоретические утверждения, касающиеся влияния "возмущений" на кластеры различных типов, получены в работе [ [ 9.13 ] ].

Опишем практический опыт реализации анализа устойчивости. Несколько алгоритмов классификации были применены к данным, полученным при проведении маркетинга образовательных услуг и приведенным в работе [ [ 9.10 ] ]. Для анализа данных были использованы широко известные алгоритмы "ближайшего соседа", "дальнего соседа" и алгоритм кластер-анализа из работы [ [ 9.8 ] ]. С содержательной точки зрения полученные разбиения отличались мало. Поэтому есть основания считать, что с помощью этих алгоритмов действительно выявлена "реальная" структура данных.

Идея устойчивости как критерия "реальности" иногда реализуется неадекватно. Так, для однопараметрических алгоритмов иногда предлагают выделять разбиения, которым соответствуют наибольшие интервалы устойчивости по параметру, т.е. наибольшие приращения параметра между очередными объединениями кластеров. Для данных работы [ [ 9.10 ] ] это предложение не дало полезных результатов - были получены различные разбиения: три алгоритма - три разбиения. И с теоретической точки зрения предложение этого специалиста несостоятельно. Покажем это.

Действительно, рассмотрим алгоритм "ближайшего соседа", использующий меру близости 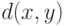, и однопараметрическое семейство алгоритмов с мерой близости 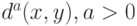, также являющихся алгоритмами "ближайшего соседа". Тогда дендрограммы, полученные с помощью этих алгоритмов, совпадают при всех , поскольку при их реализации происходит лишь сравнение мер близости между объектами. Другими словами, дендрограмма, полученная с помощью алгоритма "ближайшего соседа", является адекватной в порядковой шкале (измерения меры близости 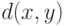), т.е. сохраняется при любом строго возрастающем преобразовании этой меры. Однако выделенные по обсуждаемому методу "устойчивые разбиения" меняются. В частности, при достаточно большом "наиболее объективным" в соответствии с рассматриваемым предложением будет, как нетрудно показать, разбиение на два кластера! Таким образом, разбиение, выдвинутое как "устойчивое", на самом деле оказывается весьма неустойчивым.