|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Проверка гипотез
7.1. Метод моментов проверки гипотез
К методу моментов относят все статистические процедуры, основанные на использовании выборочных моментов и функций от них. Метод моментов оценивания параметров распределения рассмотрен в гл.6. В непараметрической статистике на основе выборочных моментов проводится точечное и интервальное оценивание характеристик распределения, таких, как математическое ожидание, дисперсия, среднее квадратическое отклонение, коэффициент вариации ( "Статистический анализ числовых величин" ). Для проверки гипотез в непараметрической статистике также используется метод моментов. Примером является критерий Крамера-Уэлча, предназначенный для проверки равенства математических ожиданий по двум независимым выборкам ( "Статистический анализ числовых величин" ).
В практике применения статистических методов (согласно классическим схемам) довольно часто возникает необходимость проверки гипотезы о том, что функция распределения результатов наблюдений 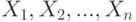 принадлежит параметрическому семейству распределений
принадлежит параметрическому семейству распределений 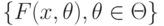 , где
, где 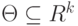 . Как проверять эту гипотезу?
. Как проверять эту гипотезу?
Давно разработан универсальный метод - критерий минимума хи-квадрат [ 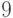 ]. Однако у него имеется существенный недостаток - необходимость группирования наблюдений, что приводит к потере информации. Как хорошо известно [
[
7.16
]
], это приводит к существенному снижению мощности критерия минимума хи-квадрат по сравнению с критериями типа Колмогорова и омега-квадрат. Кроме того, нахождение минимума статистики хи-квадрат - достаточно сложная вычислительная процедура. Поэтому иногда вместо оценок, получаемых при указанной оптимизации, подставляют оценки максимального правдоподобия или какие-либо еще. Такая замена приводит к тому, что распределение рассматриваемой статистики существенно отличается от классического, причем различие не исчезает при росте объема выборки.
Предложенная член-корр. АН СССР Л.Н. Большевым и проф. М.С. Никулиным [
[
7.3
]
] модификация критерия минимума хи-квадрат не снимает недостатков, связанных с группированием и необходимостью существенной вычислительной работы.
]. Однако у него имеется существенный недостаток - необходимость группирования наблюдений, что приводит к потере информации. Как хорошо известно [
[
7.16
]
], это приводит к существенному снижению мощности критерия минимума хи-квадрат по сравнению с критериями типа Колмогорова и омега-квадрат. Кроме того, нахождение минимума статистики хи-квадрат - достаточно сложная вычислительная процедура. Поэтому иногда вместо оценок, получаемых при указанной оптимизации, подставляют оценки максимального правдоподобия или какие-либо еще. Такая замена приводит к тому, что распределение рассматриваемой статистики существенно отличается от классического, причем различие не исчезает при росте объема выборки.
Предложенная член-корр. АН СССР Л.Н. Большевым и проф. М.С. Никулиным [
[
7.3
]
] модификация критерия минимума хи-квадрат не снимает недостатков, связанных с группированием и необходимостью существенной вычислительной работы.
Общий подход, основанный на дистанционном методе, предложен Дж. Вольфовицем (США) в 1950-х годах. Согласно этому методу следует основываться на том или ином расстоянии между эмпирической функцией распределения и параметрическим семейством распределений (как многообразием в пространстве всех функций распределения). Конкретная реализация этого подхода приводит к критериям типа Колмогорова и омега-квадрат. Однако для каждого конкретного параметрического семейства приходится разрабатывать самостоятельную теорию и рассчитывать только ему соответствующие предельные и точные распределения [ [ 7.11 ] , [ 7.20 ] ]. Предельные распределения найдены лишь для нескольких семейств, а о точных почти ничего не известно. До сих пор часто совершают ошибку, применяя для произвольных семейств предельные распределения, найденные для проверки согласия с фиксированным распределением (см. подробности в "Основы вероятностно-статистических методов описания неопределенностей" ).
Отметим, что критерии минимума хи-квадрат и аналогичные им не являются состоятельными, поскольку вероятности попадания в области группирования не задают однозначно функцию распределения. С этим недостатком можно бороться, увеличивая число интервалов группирования вместе с ростом объема выборки, однако на этом пути еще не выработаны рекомендации, пригодные для широкого практического использования. Критерии типа Колмогорова и омега-квадрат - состоятельные, т.е. любую альтернативную функцию распределения, не входящую в рассматриваемое параметрическое семейство, они отвергают с вероятностью, стремящейся к 1 при росте объема выборки.
Для конкретности обсудим проверку согласия результатов наблюдений с трехпараметрическим семейством гамма-распределений с плотностями
![f(x;a,b,c)=
\left\{
\begin{aligned}
&\frac{1}{\Gamma(a)}(x-c)^{a-1}b^{-a}\exp\left[-\frac{x-c}{b}\right],x\ge c, \\
&0,\;x<c.
\end{aligned}
\right.](/sites/default/files/tex_cache/2aa451706d53272ea796ab37746ecf0e.png) |
( 1) |
Здесь 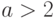 - параметр формы,
- параметр формы, 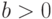 - параметр масштаба и
- параметр масштаба и  - параметр сдвига,
- параметр сдвига,  - одна из используемых в математике специальных функций, так называемая "гамма-функция". Критерий минимума хи-квадрат имеет указанные выше недостатки. Критерии типа Колмогорова и омега-квадрат для этого случая не разработаны.
- одна из используемых в математике специальных функций, так называемая "гамма-функция". Критерий минимума хи-квадрат имеет указанные выше недостатки. Критерии типа Колмогорова и омега-квадрат для этого случая не разработаны.
В подобных ситуациях целесообразно строить критерии согласия на основе функций от выборочных моментов, т.е. пользоваться методом моментов. Для оценивания параметров метод моментов хорошо известен и обычно рассматривается в учебной литературе по теории вероятностей и математической статистике. Реализацией метода моментов для проверки нормальности являются известные критерии асимметрии и эксцесса [ [ 2.1 ]
Пример 1. Если случайная величина  имеет нормальное распределение с математическим ожиданием
имеет нормальное распределение с математическим ожиданием  и дисперсией
и дисперсией  , то, как известно [
[
2.1
]
],
, то, как известно [
[
2.1
]
],
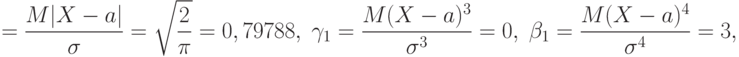
 - нормированное среднее абсолютное отклонение,
- нормированное среднее абсолютное отклонение, 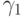 - коэффициент асимметрии и
- коэффициент асимметрии и  - коэффициент эксцесса. Таким образом, если выборочные оценки указанных моментных отношений существенно отличаются от соответствующих теоретических значений, то следует признать, что распределение результатов наблюдений отлично от нормального. Так как указанные выше значения моментных отношений могут приниматься и для распределений, отличных от нормальных, то близость выборочных значений к только что выписанным не обязательно свидетельствует о нормальности распределения результатов наблюдений. Критерии, полученные методом моментов, служат не столько для проверки нормальности, сколько для выявления отклонений распределения от нормального, или, точнее, для проверки гипотез
- коэффициент эксцесса. Таким образом, если выборочные оценки указанных моментных отношений существенно отличаются от соответствующих теоретических значений, то следует признать, что распределение результатов наблюдений отлично от нормального. Так как указанные выше значения моментных отношений могут приниматься и для распределений, отличных от нормальных, то близость выборочных значений к только что выписанным не обязательно свидетельствует о нормальности распределения результатов наблюдений. Критерии, полученные методом моментов, служат не столько для проверки нормальности, сколько для выявления отклонений распределения от нормального, или, точнее, для проверки гипотез 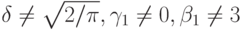 . Рассматриваемые критерии построены на основе выборочных моментных отношений:
. Рассматриваемые критерии построены на основе выборочных моментных отношений: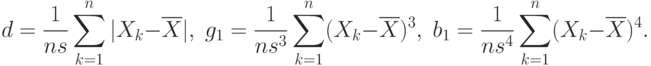
Здесь, как обычно,  - выборочное среднее арифметическое и
- выборочное среднее арифметическое и 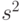 - выборочная дисперсия, соответственно,
- выборочная дисперсия, соответственно,  - выборочное среднее квадратическое отклонение. Как вытекает из результатов
"Теоретическая база прикладной статистики"
, все три статистики являются асимптотически нормальными. Выражения для параметров их асимптотических распределений приведены в [
[
2.1
]
]. Процентные точки распределений рассматриваемых выборочных моментных отношений при конечных объемах выборки найдены в предположении нормальности результатов наблюдений [
[
2.1
]
].
- выборочное среднее квадратическое отклонение. Как вытекает из результатов
"Теоретическая база прикладной статистики"
, все три статистики являются асимптотически нормальными. Выражения для параметров их асимптотических распределений приведены в [
[
2.1
]
]. Процентные точки распределений рассматриваемых выборочных моментных отношений при конечных объемах выборки найдены в предположении нормальности результатов наблюдений [
[
2.1
]
].
Как и критерии минимума хи-квадрат, критерии метода моментов никогда не являются состоятельными. Однако они, как и в случае критериев асимметрии и эксцесса, позволяют в ряде случаев отвергнуть гипотезу согласия. Использование несостоятельных критериев часто встречается в прикладной статистике. Отметим, например, что применение критерия Вилкоксона для проверки гипотезы однородности двух выборок широко распространено, хотя против общей альтернативы он является несостоятельным (см. "Статистический анализ числовых величин" ).
Критерии метода моментов основаны на использовании функций от выборочных моментов, имеющих асимптотически нормальные распределения, параметры которых легко могут быть вычислены по методике, описанной в
"Теоретическая база прикладной статистики"
. Метод моментов по сравнению с другими методами проверки согласия требует существенно меньше вычислений (число операций пропорционально объему выборки). Поэтому он может быть рекомендован для использования при проверке согласия с семействами распределений, для которых не разработаны более совершенные методы, а также в качестве быстрого (экспрессного) метода. Что же касается хорошо изученных семейств, например, нормального, то основанные на использовании моментов критерии асимметрии и эксцесса применять для проверки нормальности нецелесообразно. Судя по специальным исследованиям, следует рекомендовать критерий  Шапиро-Уилка.
Шапиро-Уилка.
Продемонстрируем применение метода моментов на примере проверки гипотезы согласия с двухпараметрическим семейством гамма-распределений без сдвига, т.е. выделяемого из семейства (1) условием 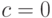 . Поскольку для трехпараметрического семейства гамма-распределений (1)
. Поскольку для трехпараметрического семейства гамма-распределений (1)
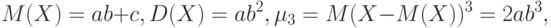
 выполнено соотношение
выполнено соотношение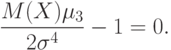 |
( 2) |
Для специалистов по техническим наукам большое значение имеет альтернативная гипотеза

В частности, она связана с дискуссией о выборе нормируемых показателей надежности технических устройств. Альтернативная гипотеза соответствует предположению, что в течение некоторого времени (до момента  ) отказы невозможны, а нулевая - связана с отрицанием этого предположения и признанием того, что отказы возможны в любой момент.
) отказы невозможны, а нулевая - связана с отрицанием этого предположения и признанием того, что отказы возможны в любой момент.
При справедливости альтернативной гипотезы
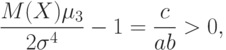
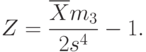
С помощью описанной в
"Теоретическая база прикладной статистики"
методики вычисления предельного распределения функции от выборочных моментов можно установить, что при  распределение статистики
распределение статистики  сходится к нормальному, причем при справедливости нулевой гипотезы, т.е. соотношения (2), асимптотическое распределение имеет нулевое математическое ожидание и дисперсию
сходится к нормальному, причем при справедливости нулевой гипотезы, т.е. соотношения (2), асимптотическое распределение имеет нулевое математическое ожидание и дисперсию
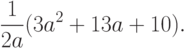 |
( 3) |
Поскольку параметр формы  неизвестен статистику, необходимо в выражении (3) заменить
неизвестен статистику, необходимо в выражении (3) заменить  на его состоятельную оценку, например, на оценку метода моментов (см.
"Оценивание"
)
на его состоятельную оценку, например, на оценку метода моментов (см.
"Оценивание"
)

Рассмотрим критерий с критической областью вида
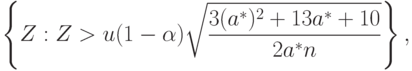 |
( 4) |
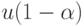 - квантиль порядка
- квантиль порядка 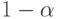 стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. При
стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. При  уровень значимости этого критерия стремится к
уровень значимости этого критерия стремится к  .
.Если альтернативная гипотеза является двусторонней, т.е. 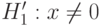 , то аналогично строится двусторонняя критическая область.
, то аналогично строится двусторонняя критическая область.
Критерий (4) состоятелен против альтернативы  , а также против непараметрической альтернативы
, а также против непараметрической альтернативы
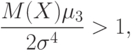
Пример 2. Применим критерий (4) для проверки согласия с гамма-распределением при 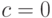 , т.е. с двухпараметрическим семейством, данных о наработке
, т.е. с двухпараметрическим семейством, данных о наработке  резцов до предельного состояния (в часах), приведенных в табл.6.2 в 6.1.
резцов до предельного состояния (в часах), приведенных в табл.6.2 в 6.1.
Для рассматриваемых данных 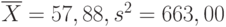 , выборочный третий центральный момент
, выборочный третий центральный момент  , откуда
, откуда 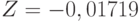 . При этом
. При этом 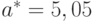 , и потому
, и потому
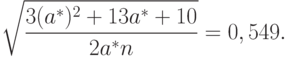
Следовательно, гипотеза согласия рассматриваемых данных с двухпараметрическим гамма-распределением не отвергается на любом из обычно используемых уровней значимости, как для односторонней критической области, так и для двухсторонней.
