|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Проверка гипотез
Пример 2. Пусть  при
при  и
и  . Пусть
. Пусть 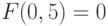 , т.е. предельное распределение сосредоточено на [1/2; 1]. Пусть распределение
, т.е. предельное распределение сосредоточено на [1/2; 1]. Пусть распределение  на [0; 1/2) имеет единственный атом в точке
на [0; 1/2) имеет единственный атом в точке  величиной
величиной  , а на [1/2; 1] справедливо (10). Тогда по причинам, изложенным при доказательстве теоремы 1,
, а на [1/2; 1] справедливо (10). Тогда по причинам, изложенным при доказательстве теоремы 1,
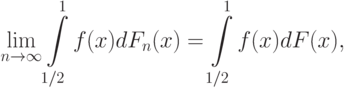
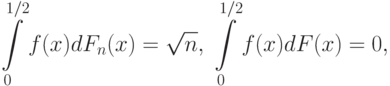
Условие ограниченности подынтегральной функции  можно заменить, как это сделано, например, в [13], на условие строгого возрастания функции распределения
можно заменить, как это сделано, например, в [13], на условие строгого возрастания функции распределения  .
.
Лемма. Пусть функции распределения  всюду строго возрастает, т.е. из
всюду строго возрастает, т.е. из 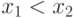 вытекает
вытекает 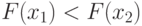 . Пусть функция
. Пусть функция  интегрируема по Риману-Стилтьесу по
интегрируема по Риману-Стилтьесу по  , т.е. выполнено (14). Тогда функция
, т.е. выполнено (14). Тогда функция  ограничена.
ограничена.
Доказательство. Рассмотрим точки 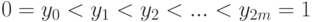 и два разбиения
и два разбиения
![T_1\{[0;y_1),[y_1;y_3)[y_3;y_5),...,[y_{2m-1};1]\},
T_2\{[0;y_2),[y_2;y_4)[y_4;y_6),...,[y_{2m-2};1]\},](/sites/default/files/tex_cache/ce486c07184ee29052319240f5a8760e.png)
Тогда для любых двух точек  и
и 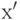 можно указать конечную последовательность точек
можно указать конечную последовательность точек 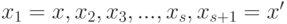 такую, что любые две соседние точки
такую, что любые две соседние точки  , одновременно принадлежат некоторому элементу
, одновременно принадлежат некоторому элементу 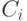 разбиения
разбиения 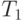 или разбиения
или разбиения 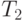 , причем
, причем  при
при 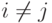 . Действительно, пусть
. Действительно, пусть  . Пусть для определенности
. Пусть для определенности 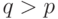 . Тогда можно положить
. Тогда можно положить 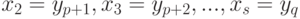 . Поскольку среди элементов разбиений
. Поскольку среди элементов разбиений 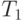 и
и 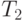 есть
есть 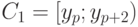 , то
, то 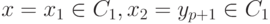 . Далее,
. Далее, 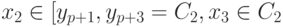 , и т.д.
, и т.д.
Из указанных выше свойств последовательности 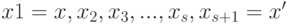 следует, что
следует, что
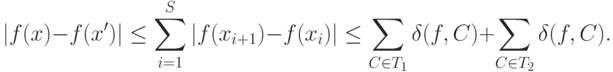
Пусть теперь число 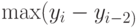 настолько мало, что согласно (14)
настолько мало, что согласно (14)
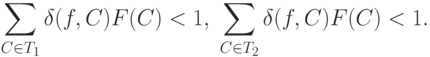
Тогда согласно двум последним соотношениям
![|f(x)-f(x')|\le 2[\min\{F(C):C\in T_1\cup T_2\}]^{-1},](/sites/default/files/tex_cache/8540aa7d9195b118205851d5580f3115.png)
Доказательство теоремы 2. Пусть условие (14) не выполнено, т.е. существуют число 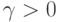 и последовательность разбиений
и последовательность разбиений  ., такие, что
., такие, что 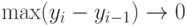 при
при 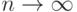 и при всех
и при всех 
 |
( 20) |
Для доказательства теоремы построим две последовательности функций распределения  и
и  ., для которых выполнено (10), но последовательность
., для которых выполнено (10), но последовательность
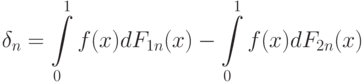
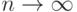 . Тогда (11) не выполнено хотя бы для одной из последовательностей
. Тогда (11) не выполнено хотя бы для одной из последовательностей  и
и  .
.Для любого  - элемента некоторого разбиения
- элемента некоторого разбиения 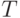 - можно указать, как вытекает из определения
- можно указать, как вытекает из определения 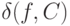 , точки
, точки 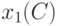 и
и 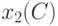 такие, что
такие, что
 |
( 21) |
Построим  и
и  следующим образом. Пусть
следующим образом. Пусть 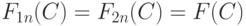 для любого
для любого  из
из 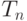 . При этом
. При этом  имеет в
имеет в  один атом в точке
один атом в точке 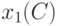 величиной
величиной 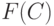 , а
, а  имеет в
имеет в  также один атом в точке
также один атом в точке 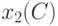 той же величины
той же величины 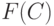 . Другими словами, распределение
. Другими словами, распределение  в
в  сосредоточено в одной точке, а именно, в
сосредоточено в одной точке, а именно, в 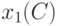 , а распределение
, а распределение  сосредоточено в
сосредоточено в 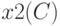 . Тогда
. Тогда
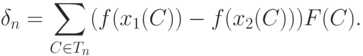 |
( 22) |
Из (20), (21) и (22) следует, что
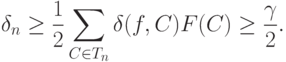
Остается показать, что для последовательностей функций распределения  и
и  выполнено (10). Пусть
выполнено (10). Пусть  - точка непрерывности
- точка непрерывности  . Пусть
. Пусть
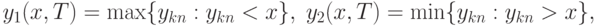
 - точки, определяющие разбиения
- точки, определяющие разбиения 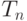 согласно (12). В соответствии с определением
согласно (12). В соответствии с определением 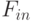
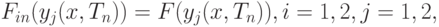
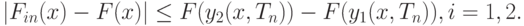
В силу условия 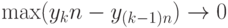 и непрерывности
и непрерывности  в точке
в точке  правая часть последнего соотношения стремится к 0 при
правая часть последнего соотношения стремится к 0 при 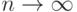 , что и заканчивает доказательство теоремы 2.
, что и заканчивает доказательство теоремы 2.
Теоремы 1 и 2 демонстрируют основные идеи предельной теории статистик интегрального типа и непараметрических критериев в целом. Как показывают эти теоремы, основную роль в рассматриваемой теории играет предельное соотношение (14). Отметим, что если 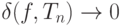 при
при 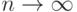 , то (14) справедливо, но, вообще говоря, не наоборот. Естественно возникает еще ряд постановок. Пусть (14) выполнено для
, то (14) справедливо, но, вообще говоря, не наоборот. Естественно возникает еще ряд постановок. Пусть (14) выполнено для 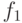 и
и  . При каких функциях
. При каких функциях  это соотношение выполнено для
это соотношение выполнено для 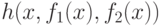 ? В прикладной статистике вместо
? В прикладной статистике вместо  рассматривают
рассматривают  и
и  , а вместо интегрирования по функциям распределения
, а вместо интегрирования по функциям распределения 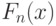 - интегрирование по случайным мерам
- интегрирование по случайным мерам 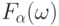 .
Как меняются формулировки в связи с такой заменой? В связи со слабой сходимостью (т.е. сходимостью по распределению)
.
Как меняются формулировки в связи с такой заменой? В связи со слабой сходимостью (т.е. сходимостью по распределению) 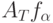 к
к  и переходом от
и переходом от  к
к 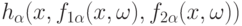 возникает следующая постановка. Пусть
возникает следующая постановка. Пусть  слабо сходится к
слабо сходится к 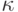 при
при  . Когда распределения
. Когда распределения 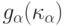 сближаются с распределениями
сближаются с распределениями 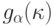 ? Полным ответом на последний вопрос являются необходимые и достаточные условия наследования сходимости. Они приведены в
"Теоретическая база прикладной статистики"
.
? Полным ответом на последний вопрос являются необходимые и достаточные условия наследования сходимости. Они приведены в
"Теоретическая база прикладной статистики"
.
Основные результаты. Наиболее общая теорема типа теоремы 1 выглядит так [ [ 4.19 ] ].
Теорема 3. Пусть существует последовательность разбиений  ., такая, что при
., такая, что при 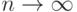 и
и  (сходимость по вероятности)
(сходимость по вероятности)
 |
( 23) |
Пусть для любого  , входящего хотя бы в одно из разбиений
, входящего хотя бы в одно из разбиений 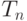 ,
,
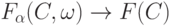 |
( 24) |
 (сходимость по вероятности). Пусть
(сходимость по вероятности). Пусть 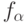 асимптотически ограничены по вероятности при
асимптотически ограничены по вероятности при  . Тогда
. Тогда |
( 25) |
 (сходимость по вероятности).
(сходимость по вероятности).Как известно, полное сепарабельное метрическое пространство называется польским. Это понятие понадобится для формулировки аналога теоремы 2.
Теорема 4. Пусть  - польское пространство,
- польское пространство,  конечномерно, существует измельчающаяся последовательность
конечномерно, существует измельчающаяся последовательность 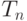 разбиений, для которой соотношение (23) не выполнено. Тогда существует удовлетворяющая (24) последовательность
разбиений, для которой соотношение (23) не выполнено. Тогда существует удовлетворяющая (24) последовательность 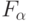 , для которой соотношение (25) неверно, хотя
, для которой соотношение (25) неверно, хотя 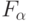 слабо сходится к
слабо сходится к  при
при  .
.
Условие (23) естественно назвать условием римановости, поскольку в случае, рассмотренном в теореме 1, оно является условием интегрируемости по Риману-Стилтьесу. Рассмотрим наследуемость римановости при переходе от 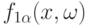 со значениями в
со значениями в 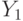 и
и 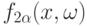 со значениями в
со значениями в 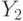 , удовлетворяющих (23), к
, удовлетворяющих (23), к 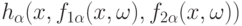 со значениями в
со значениями в 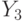 .
.
Положим
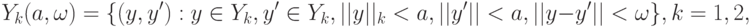
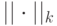 - норма (т.е. длина вектора) в пространстве
- норма (т.е. длина вектора) в пространстве 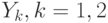 . Рассмотрим также множества
. Рассмотрим также множества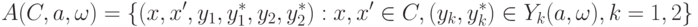
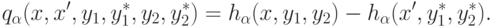
Наконец, понадобится измеритель колеблемости


Теорема 5. Пусть 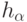 асимптотически (при
асимптотически (при  ) ограничены на
) ограничены на  при любом положительном
при любом положительном  , функции
, функции 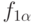 и
и 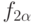 асимптотически ограничены по вероятности и удовлетворяют условию (23). Пусть для участвующей в (23) последовательности
асимптотически ограничены по вероятности и удовлетворяют условию (23). Пусть для участвующей в (23) последовательности 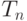
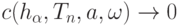 |
( 26) |
 и любом положительном
и любом положительном  . Тогда
. Тогда  удовлетворяют условию (23) и асимптотически ограничены по вероятности.
удовлетворяют условию (23) и асимптотически ограничены по вероятности.Теорема 6. Пусть условие (26) не выполнено для 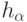 . Тогда существуют детерминированные ограниченные функции
. Тогда существуют детерминированные ограниченные функции 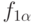 и
и 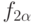 такие, что соотношение (23) выполнено для
такие, что соотношение (23) выполнено для 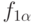 и
и 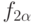 и не выполнено для
и не выполнено для 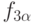 .
.
Пример 3. Пусть ![X = [0; 1]^k](/sites/default/files/tex_cache/134725ab4f90a515de832399117f7027.png) , пространства
, пространства 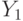 и
и 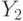 конечномерны, функция
конечномерны, функция 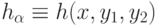 непрерывна. Тогда условие (26) выполнено.
непрерывна. Тогда условие (26) выполнено.
С помощью теорем 3 и 5 и результатов о наследовании сходимости можно изучить асимптотическое поведение статистик интегрального типа
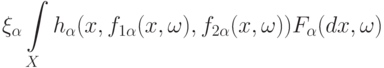
 .
.Теорема 7. Пусть для некоторой последовательности 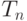 разбиений
разбиений  справедливы соотношения (23) для
справедливы соотношения (23) для 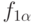 и
и 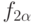 и (24) для
и (24) для 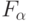 . Пусть последовательность функций
. Пусть последовательность функций 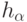 удовлетворяет условию в теореме 5, конечномерные распределения
удовлетворяет условию в теореме 5, конечномерные распределения 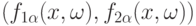 слабо сходятся к конечномерным распределениям
слабо сходятся к конечномерным распределениям 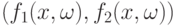 , причем для
, причем для 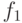 и
и  справедливо соотношение (23). Тогда
справедливо соотношение (23). Тогда

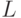 - расстояние Прохорова (см. 4.3),
- расстояние Прохорова (см. 4.3),
Теорема 7 дает общий метод получения асимптотических распределений статистик интегрального типа. Важно, что соотношение (23) выполнено для эмпирического процесса и для процессов, связанных с оцениванием параметров при проверке согласия [ [ 4.19 ] ].
Один из выводов общей теории состоит в том, что в качестве 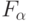 можно использовать практически любую состоятельную оценку истинной функции распределения. Этот вывод использовался при построении критерия типа омега-квадрат для проверки симметрии распределения относительно 0 и обнаружения различий в связанных выборках (
"Статистический анализ числовых величин"
).
можно использовать практически любую состоятельную оценку истинной функции распределения. Этот вывод использовался при построении критерия типа омега-квадрат для проверки симметрии распределения относительно 0 и обнаружения различий в связанных выборках (
"Статистический анализ числовых величин"
).
Асимптотическое поведение критериев типа Колмогорова может быть получено с помощью описанного выше метода аппроксимации ступенчатыми функциями. Этот метод не требует обращения к теории сходимости вероятностных мер в функциональных пространствах. Для критериев Колмогорова и Смирнова достаточно использовать лишь свойства эмпирического процесса и броуновского моста. В случае проверки согласия добавляется необходимость изучения еще одного случайного процесса. Он является разностью между двумя функциями распределения. Одна - функция распределения элементов выборки. Вторая - случайный член параметрического семейства распределений, полученный путем подстановки оценок параметров вместо их истинных значений.
