|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Проверка гипотез
7.3. Предельная теория непараметрических критериев
В прикладной статистике широко используются статистики типа омега-квадрат и типа Колмогорова-Смирнова. Они применяются для проверки согласия с фиксированным распределением или семейством распределений, для проверки однородности двух выборок, симметрии распределения относительно 0, при оценивании условной плотности и регрессии в пространствах произвольной природы и т.д.
Статистики интегрального типа и их асимптотика. Рассмотрим статистики интегрального типа
 |
( 1) |
где  - некоторое пространство, по которому происходит интегрирование (например,
- некоторое пространство, по которому происходит интегрирование (например, ![X=[0; 1], X=R^1](/sites/default/files/tex_cache/a6ef2f04c891f1375e225c4f23bb9d13.png) или
или  ). Здесь
). Здесь  - направленное множество, переход к пределу по которому обозначен как
- направленное множество, переход к пределу по которому обозначен как  (см.
"Теоретическая база прикладной статистики"
). Случайные функции
(см.
"Теоретическая база прикладной статистики"
). Случайные функции  обычно принимают значения, являющиеся числами. Но иногда рассматривают и постановки, в которых
обычно принимают значения, являющиеся числами. Но иногда рассматривают и постановки, в которых 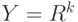 или
или  - банахово пространство (т.е. полное нормированное пространство [
[
1.9
]
]). Наконец,
- банахово пространство (т.е. полное нормированное пространство [
[
1.9
]
]). Наконец,  - случайная функция распределения или случайная вероятностная мера; в последнем случае используют также обозначение
- случайная функция распределения или случайная вероятностная мера; в последнем случае используют также обозначение  .
.
Предполагаются выполненными необходимые для корректности внутриматематические предположения измеримости, например, сформулированные в [ [ 4.19 ] , [ 4.19 ] ].
Пример 1. Рассмотрим критерий Лемана-Розенблатта, т.е. критерий типа омега-квадрат для проверки однородности двух независимых выборок (см. "Статистический анализ числовых величин" ). Его статистика имеет вид:

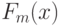 - эмпирическая функция распределения, построенная по первой выборке объема
- эмпирическая функция распределения, построенная по первой выборке объема 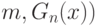 - эмпирическая функция распределения, построенная по второй выборке объема
- эмпирическая функция распределения, построенная по второй выборке объема  , а
, а  - эмпирическая функция распределения, построенная по объединенной выборке объема
- эмпирическая функция распределения, построенная по объединенной выборке объема  . Легко видеть, что
. Легко видеть, что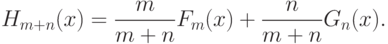
Ясно, что статистика  имеет вид (1). При этом
имеет вид (1). При этом  - действительное число,
- действительное число, 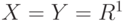 , в роли
, в роли  выступает пара
выступает пара 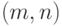 , и
, и  означает, что
означает, что 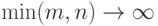 . Далее,
. Далее,

Наконец, 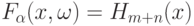 .
.
Теперь обсудим асимптотическое поведение функций  и
и 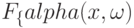 , с помощью которых определяется статистика
, с помощью которых определяется статистика  . Ограничимся случаем, когда справедлива гипотеза однородности, функции распределения, соответствующие генеральным совокупностям, из которых взяты выборки, совпадают. Их общую функцию распределения обозначим
. Ограничимся случаем, когда справедлива гипотеза однородности, функции распределения, соответствующие генеральным совокупностям, из которых взяты выборки, совпадают. Их общую функцию распределения обозначим 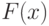 . Она предполагается непрерывной. Введем в рассмотрение выборочные процессы
. Она предполагается непрерывной. Введем в рассмотрение выборочные процессы

Нетрудно проверить, что
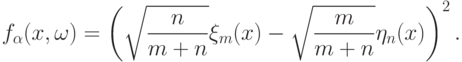
Сделаем замену переменной 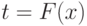 . Тогда выборочные процессы переходят в соответствующие эмпирические (см.
"Теоретическая база прикладной статистики"
):
. Тогда выборочные процессы переходят в соответствующие эмпирические (см.
"Теоретическая база прикладной статистики"
):
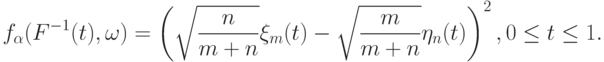
Конечномерные распределения этого процесса, т.е. распределения случайных векторов
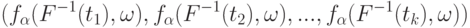
 , сходятся к конечномерным распределениям квадрата броуновского моста
, сходятся к конечномерным распределениям квадрата броуновского моста  . В соответствии с
. В соответствии с  4.5 рассматриваемая сходимость по распределению обозначается так:
4.5 рассматриваемая сходимость по распределению обозначается так: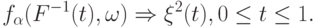 |
( 2) |
Нетрудно видеть, что
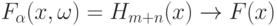
 . С помощью замены переменной
. С помощью замены переменной 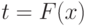 получаем, что
получаем, что |
( 3) |
 . Из соотношений (2) и (3) хотелось бы сделать вывод, что в случае статистики Лемана - Розенблатта типа омега-квадрат
. Из соотношений (2) и (3) хотелось бы сделать вывод, что в случае статистики Лемана - Розенблатта типа омега-квадрат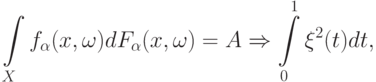
т.е. предельным распределением этой статистики является классическое распределение Смирнова [ [ 2.1 ] ], найденное как предельное для одновыборочной статистики критерия согласия омега-квадрат Крамера-Мизеса-Смирнова.
Действительно, сформулированное утверждение справедливо. Однако доказательство нетривиально.
Так, может показаться очевидным следующее утверждение.
Утверждение 1. Пусть ![f: [0; 1] \rightarrow R^1](/sites/default/files/tex_cache/e9f83ee492fdeedc47c429db65cb90ff.png) - ограниченная функция,
- ограниченная функция,  и
и  - функции распределения,
- функции распределения,  , причем
, причем 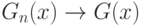 при всех
при всех  . Тогда
. Тогда
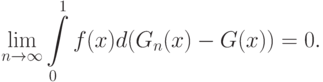 |
( 4) |
Это утверждение неверно (ср. [  , с.42]). Действительно, пусть
, с.42]). Действительно, пусть 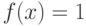 , если
, если  рационально, и
рационально, и 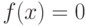 , если
, если  иррационально,
иррационально, 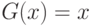 , а кусочно-постоянные функции
, а кусочно-постоянные функции  имеют скачки величиной
имеют скачки величиной 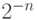 в точках
в точках  при всех
при всех  . Тогда
. Тогда 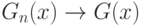 при всех
при всех  , однако
, однако

 . Следовательно, вопреки сформулированному выше утверждению 1,
. Следовательно, вопреки сформулированному выше утверждению 1,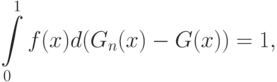
Итак, сформулируем проблему. Пусть известно, что последовательность случайных функций 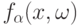 сходится по распределению при
сходится по распределению при  к случайной функции
к случайной функции 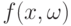 . Пусть последовательность случайных мер
. Пусть последовательность случайных мер 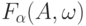 сходится по распределению к вероятностной мере
сходится по распределению к вероятностной мере  при
при  . Если речь идет о конечномерном пространстве и меры задаются функциями распределения, то сходимость
. Если речь идет о конечномерном пространстве и меры задаются функциями распределения, то сходимость 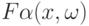 к
к 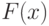 должна иметь место во всех точках непрерывности
должна иметь место во всех точках непрерывности 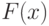 . В каких случаях можно утверждать, что при
. В каких случаях можно утверждать, что при  справедлив предельный переход
справедлив предельный переход
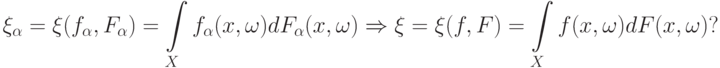
Выше показано, что, например, ограниченности  для этого недостаточно.
для этого недостаточно.
Метод аппроксимации ступенчатыми функциями. Пусть 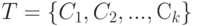 - разбиение пространства
- разбиение пространства  на непересекающиеся подмножества. Пусть в каждом элементе
на непересекающиеся подмножества. Пусть в каждом элементе 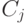 разбиения
разбиения 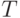 выделена точка
выделена точка 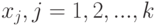 . На множестве функций
. На множестве функций 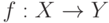 введем оператор
введем оператор  : если
: если  , то
, то
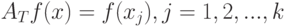 |
( 5) |
Тогда 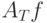 - аппроксимация функции
- аппроксимация функции  ступенчатыми (кусочно-постоянными) функциями.
ступенчатыми (кусочно-постоянными) функциями.
Пусть  - последовательность случайных функций на
- последовательность случайных функций на  , а
, а 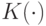 - функционал на множестве всех возможных их траекторий как функций от
- функционал на множестве всех возможных их траекторий как функций от  . Для изучения распределения
. Для изучения распределения 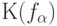 методом аппроксимации ступенчатыми функциями используют разложение
методом аппроксимации ступенчатыми функциями используют разложение
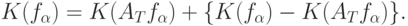 |
( 6) |
Согласно (5) распределение первого слагаемого в (6) определяется конечномерным распределением случайного элемента, а именно, распределением вектора
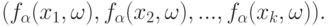 |
( 7) |
В обычных постановках предельной теории непараметрических критериев распределение вектора (7) сходится при  к соответствующему конечномерному распределению предельной случайной функции
к соответствующему конечномерному распределению предельной случайной функции 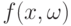 , т.е. к распределению случайного вектора
, т.е. к распределению случайного вектора
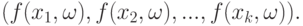 |
( 8) |
В соответствии с теорией наследования сходимости (
"Теоретическая база прикладной статистики"
) при слабых условиях на функционал 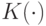 из сходимости по распределению вектора (7) к вектору (8) следует сходимость по распределению
из сходимости по распределению вектора (7) к вектору (8) следует сходимость по распределению 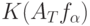 к
к 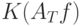 .
.
Используя аналогичное (6) разложение
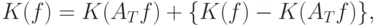 |
( 9) |
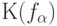 к
к 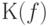 при
при  в два этапа: сначала выбрать разбиение
в два этапа: сначала выбрать разбиение 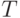 так, чтобы вторые слагаемые в правых частях соотношений (6) и (9) были малы, а затем при фиксированном операторе
так, чтобы вторые слагаемые в правых частях соотношений (6) и (9) были малы, а затем при фиксированном операторе  воспользоваться сходимостью по распределению
воспользоваться сходимостью по распределению  к
к  .
.Рассмотрим простой пример применения метода аппроксимации ступенчатыми функциями.
Обобщение теоремы Хелли. Пусть ![f: [0;1]\rightarrow R^1](/sites/default/files/tex_cache/6802a6e01844eccbbff840c4751f47c7.png) - измеримая функция,
- измеримая функция, 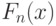 - функции распределений, сосредоточенных на отрезке
- функции распределений, сосредоточенных на отрезке ![[0; 1]](/sites/default/files/tex_cache/f083648758df2ddf9560f0b17ac28d3b.png) . Пусть
. Пусть 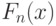 сходятся в основном к функции распределения
сходятся в основном к функции распределения 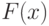 , т.е.
, т.е.
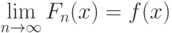 |
( 10) |
для всех  , являющихся точками непрерывности
, являющихся точками непрерывности 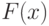 .
.
Утверждение 2. Если  - непрерывная функция, то
- непрерывная функция, то
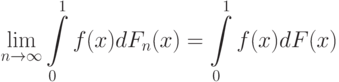 |
( 11) |
Утверждение 2 известно в литературе как первая теорема Хелли [ [ 1.9 ] , с.344-346], вторая теорема Хелли [ [ 2.3 ] , с.174-175], лемма Хелли-Брея [ [ 7.10 ] , с.193-194].
Естественно поставить вопрос: при каких  из (10) следует (11)? Необходимо ввести условия и на
из (10) следует (11)? Необходимо ввести условия и на 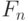 : если
: если  , то соотношение (11) верно для любой измеримой функции
, то соотношение (11) верно для любой измеримой функции  , для которой интеграл в (11) существует. Поэтому рассмотрим следующую постановку.
, для которой интеграл в (11) существует. Поэтому рассмотрим следующую постановку.
Постановка 1. Пусть функция  такова, что для любой последовательности
такова, что для любой последовательности 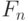 , удовлетворяющей (10), справедливо (11). Что можно сказать о функции
, удовлетворяющей (10), справедливо (11). Что можно сказать о функции  ?
?
В работах [
[
4.19
]
,
[
4.19
]
] найдены следующие необходимые и достаточные условия на функцию  .
.
Теорема 1. Пусть ограниченная на [0; 1] функция  интегрируема по Риману-Стилтьесу по функции распределения
интегрируема по Риману-Стилтьесу по функции распределения 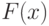 . Тогда для любой последовательности функций распределения
. Тогда для любой последовательности функций распределения 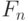 , сходящейся в основном к
, сходящейся в основном к  , имеет место предельный переход (11).
, имеет место предельный переход (11).
Теорема 2. Пусть функция  не интегрируема по Риману-Стилтьесу по функции распределения
не интегрируема по Риману-Стилтьесу по функции распределения 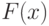 . Тогда существует последовательность функций распределения
. Тогда существует последовательность функций распределения 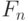 , сходящаяся в основном к
, сходящаяся в основном к  , для которой соотношение (11) не выполнено.
, для которой соотношение (11) не выполнено.
Теоремы 1 и 2 в совокупности дают необходимые и достаточные условия для  в постановке 1. А именно, необходимо и достаточно, чтобы ограниченная на [0; 1] функция
в постановке 1. А именно, необходимо и достаточно, чтобы ограниченная на [0; 1] функция  была интегрируема по Риману-Стилтьесу по
была интегрируема по Риману-Стилтьесу по  .
.
Напомним определение интегрируемости функции  по Риману-Стилтьесу по функции распределения
по Риману-Стилтьесу по функции распределения  [
[
1.9
]
, с.341]. Рассмотрим разбиение
[
[
1.9
]
, с.341]. Рассмотрим разбиение 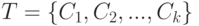 , где
, где
![C_i=[y_{i-1},y_i), i=1,2,...,m-1, C_m=[y_{m-1},y_m],](/sites/default/files/tex_cache/935d734996c89b49c14b28758e5350c7.png) |
( 12) |
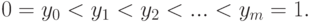
Выберем в 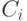 произвольную точку
произвольную точку 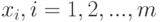 , и составим сумму
, и составим сумму
![S(T)=\sum_{i=1}^m f(x_i)[F(y_i)-F(y_{i-1})].](/sites/default/files/tex_cache/47f30d50287400a7ba37af1e69bc122c.png)
Если при  эти суммы стремятся к некоторому пределу (не зависящему ни от способа дробления отрезка [0; 1], ни от выбора точек
эти суммы стремятся к некоторому пределу (не зависящему ни от способа дробления отрезка [0; 1], ни от выбора точек  в каждом из элементов разбиения), то этот предел называется интегралом Римана-Стилтьеса от функции
в каждом из элементов разбиения), то этот предел называется интегралом Римана-Стилтьеса от функции  по функции
по функции  по отрезку [0; 1] и обозначается символом, приведенным в правой части равенства (11).
по отрезку [0; 1] и обозначается символом, приведенным в правой части равенства (11).
Рассмотрим суммы Дарбу-Стилтьеса
![S_H(T)=\sum_{i=1}^m m_i[F(y_i)-F(y_{i-1})], \;
S_B(T)=\sum_{i=1}^m M_i[F(y_i)-F(y_{i-1})],](/sites/default/files/tex_cache/745158214da11cfcba3e0505ad53cd81.png)
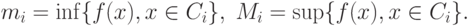
Ясно, что
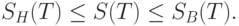
Необходимым и достаточным условием интегрируемости по Риману-Стилтьесу является следующее: для любой последовательности разбиений  . вида (12) такой, что
. вида (12) такой, что 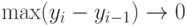 при
при 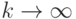 , имеем
, имеем
![\lim_{k\rightarrow\infty}[S_B(T_k)-S_H(T_k)]=0.](/sites/default/files/tex_cache/38125ef7d4e9d307cb627d8bd15cca91.png) |
( 13) |
Напомним, что согласно  4.3 колебанием
4.3 колебанием 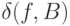 функции
функции  на множестве
на множестве  называется
называется 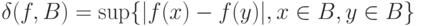 . Поскольку
. Поскольку
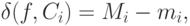
 |
( 14) |
Условие (14), допускающее обобщение с ![Х = [0; 1]](/sites/default/files/tex_cache/184cad1d65be0c352c8f1456a6fbdac2.png) и
и ![f: [0; 1] \rightarrow R^1](/sites/default/files/tex_cache/e9f83ee492fdeedc47c429db65cb90ff.png) на
на  и
и  более общего вида, и будем использовать при доказательстве теорем 1 и 2.
более общего вида, и будем использовать при доказательстве теорем 1 и 2.
Доказательство теоремы 1. Согласно методу аппроксимации ступенчатыми функциями рассмотрим оператор  . Как легко проверить, имеет место разложение
. Как легко проверить, имеет место разложение
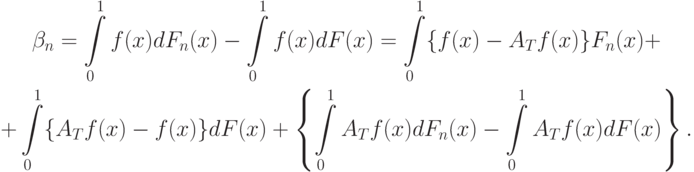 |
( 15) |
Поскольку

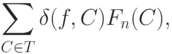 |
( 16) |
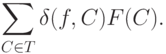
Согласно определению оператора  третье слагаемое в (15) имеет вид
третье слагаемое в (15) имеет вид

Очевидно, оно не превосходит по модулю

 на
на  ).
).Согласно (16) первое слагаемое в правой части (15) не превосходит

Поскольку
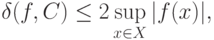
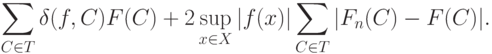
Из оценок, относящихся к трем слагаемым в разложении (15), следует, что
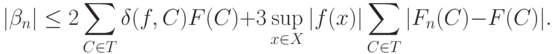 |
( 17) |
Используя оценку (17), докажем, что 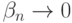 при
при 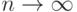 . Пусть дано
. Пусть дано 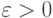 . Согласно условию интегрируемости функции
. Согласно условию интегрируемости функции  по Риману-Стилтьесу, т.е. условию (14), можно указать разбиение
по Риману-Стилтьесу, т.е. условию (14), можно указать разбиение 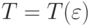 такое, что
такое, что
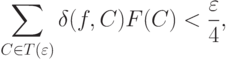 |
( 18) |
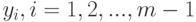 (см. (12)), функция
(см. (12)), функция  непрерывна.
непрерывна.Поскольку
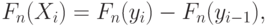
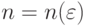 такое, что при
такое, что при 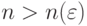 справедливо неравенство
справедливо неравенство |
( 19) |
Из (17), (18) и (19) следует, что при 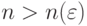 справедливо неравенство
справедливо неравенство

Обсудим условие ограниченности  . Если оно не выполнено, то из (10) не всегда следует (11).
. Если оно не выполнено, то из (10) не всегда следует (11).
