|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Выборочные исследования
3.3. Проверка однородности двух биномиальных выборок
Проверка однородности - одна из базовых проблем прикладной статистики. Она часто обсуждается в литературе, а методы проверки однородности применяются при решении многих практических задач. Например, как сравнить две группы - мужчин и женщин, молодых и пожилых, и т.п.? В маркетинге это важно для сегментации рынка. Если две группы не отличаются по ответам, значит, их можно объединить в один сегмент и проводить по отношению к ним одну и туже маркетинговую политику, в частности, осуществлять одни и те же рекламные воздействия. Если же две группы различаются, то и относиться к ним надо по-разному. Это - представители двух разных сегментов рынка, требующих разного подхода при борьбе за их завоевание.
Обсуждаемая далее постановка задачи в терминах прикладной статистики такова. Рассматривается вопрос с двумя возможными ответами, например, "да" и "нет". В первой группе из  опрошенных
опрошенных  человек сказали "да", а во второй группе из
человек сказали "да", а во второй группе из 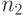 опрошенных
опрошенных 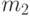 сказали "да". В вероятностной модели предполагается, что
сказали "да". В вероятностной модели предполагается, что  и
и 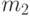 - биномиальные случайные величины
- биномиальные случайные величины  и
и  соответственно. (Запись
соответственно. (Запись 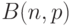 означает, что случайная величина
означает, что случайная величина  , имеющая биномиальное распределение
, имеющая биномиальное распределение 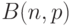 с параметрами
с параметрами  - объем выборки и
- объем выборки и  - вероятность определенного ответа (скажем, ответа "да"), может быть представлена в виде
- вероятность определенного ответа (скажем, ответа "да"), может быть представлена в виде  где случайные величины
где случайные величины  независимы, одинаково распределены, принимают два значения 1 и 0, причем
независимы, одинаково распределены, принимают два значения 1 и 0, причем 
Однородность двух групп означает, что соответствующие им вероятности равны, неоднородность - что эти вероятности отличаются. В терминах прикладной математической статистики необходимо проверить гипотезу однородности

(Иногда представляют интерес односторонние альтернативные гипотезы 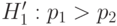 и
и 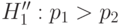 .)
.)
Оценкой вероятности 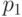 является частота
является частота 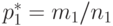 , а оценкой вероятности
, а оценкой вероятности 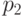 - частота
- частота  . Даже при совпадении вероятностей
. Даже при совпадении вероятностей 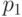 и
и 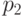 частоты, как правило, различаются. Как говорят, "по чисто случайным причинам". Рассмотрим случайную величину
частоты, как правило, различаются. Как говорят, "по чисто случайным причинам". Рассмотрим случайную величину  . Тогда
. Тогда
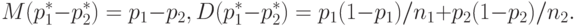
Из теоремы Муавра-Лапласа и теоремы о наследовании сходимости ( "Теоретическая база прикладной статистики" и [ [ 3.6 ] , п.2.4]) следует, что
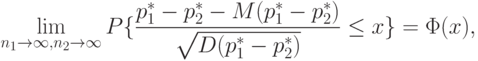
 - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Для практического применения этого соотношения следует заменить неизвестную статистику дисперсию разности частот на оценку этой дисперсии:
- функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Для практического применения этого соотношения следует заменить неизвестную статистику дисперсию разности частот на оценку этой дисперсии:
(Могут использоваться и другие оценки рассматриваемой дисперсии, например, по объединенной выборке). С помощью указанной выше математической техники можно показать, что

При справедливости гипотезы однородности 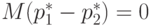 . Поэтому правило принятия решения при проверке однородности двух выборок выглядит так:
. Поэтому правило принятия решения при проверке однородности двух выборок выглядит так:
- Вычислить статистику
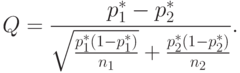
- Сравнить значение модуля статистика
 с граничным значением
с граничным значением  . Если
. Если  , то принять гипотезу однородности
, то принять гипотезу однородности  . Если же
. Если же  , то заявить об отсутствии однородности и принять альтернативную гипотезу
, то заявить об отсутствии однородности и принять альтернативную гипотезу  .
.
Граничное значение  определяется выбором уровня значимости статистического критерия проверки однородности. Из приведенных выше предельных соотношений следует, что при справедливости гипотезы однородности
определяется выбором уровня значимости статистического критерия проверки однородности. Из приведенных выше предельных соотношений следует, что при справедливости гипотезы однородности  имеем для уровня значимости
имеем для уровня значимости  (при
(при 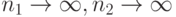 )
)

Следовательно, граничное значение (асимптотическое) в зависимости от уровня значимости целесообразно выбирать из условия

Здесь 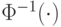 - функция, обратная к функции стандартного нормального распределения. В социально-экономических исследованиях наиболее распространен 5% уровень значимости, т.е.
- функция, обратная к функции стандартного нормального распределения. В социально-экономических исследованиях наиболее распространен 5% уровень значимости, т.е.  . Для него
. Для него  .
.
Пример 2. Пусть в первой группе из 500 опрошенных ответили "да" 200, а во второй группе из 700 опрошенных - 350. Есть ли разница между генеральными совокупностями, представленными этими двумя группами, по доле отвечающих "да"?
Уберем из формулировки примера термин "генеральная совокупность". Получим следующую постановку.
Пусть из 500 опрошенных мужчин ответили "да, я люблю пепси-колу" 200, а из 700 опрошенных женщин 350 сказали "да, я люблю пепси-колу". Есть ли разница между мужчинами и женщинами по доле отвечающих "да" на вопрос о любви к пепси-коле?
В рассматриваемом примере нужные для расчетов величины таковы:  . Вычислим статистику
. Вычислим статистику
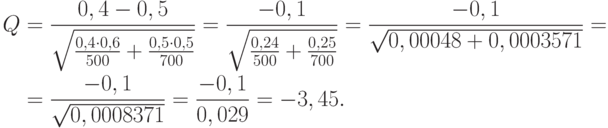
Поскольку 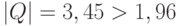 , то необходимо отклонить нулевую гипотезу и принять альтернативную. Таким образом, мужчины и женщины отличаются по рассматриваемому признаку - любви к пепси-коле.
, то необходимо отклонить нулевую гипотезу и принять альтернативную. Таким образом, мужчины и женщины отличаются по рассматриваемому признаку - любви к пепси-коле.
Необходимо отметить, что результат проверки гипотезы однородности зависит не только от частот, но и от объемов выборок. Предположим, что частоты (доли) зафиксированы, а объемы выборок растут. Тогда числитель статистики  не меняется, а знаменатель уменьшается, значит, вся дробь возрастает. Поскольку знаменатель стремится к 0, то дробь возрастает до бесконечности и рано или поздно превзойдет любую границу. Есть только одно исключение - когда в числителе стоит 0. Следовательно, при строгом подходе к формулировкам вывод статистика должен выглядеть так: "различие обнаружено" или "различие не обнаружено". Во втором случае различие, возможно, было бы обнаружено при увеличении объемов выборок.
не меняется, а знаменатель уменьшается, значит, вся дробь возрастает. Поскольку знаменатель стремится к 0, то дробь возрастает до бесконечности и рано или поздно превзойдет любую границу. Есть только одно исключение - когда в числителе стоит 0. Следовательно, при строгом подходе к формулировкам вывод статистика должен выглядеть так: "различие обнаружено" или "различие не обнаружено". Во втором случае различие, возможно, было бы обнаружено при увеличении объемов выборок.
Как и для доверительного оценивания вероятности, во ВЦИОМ разработаны две полезные таблицы, позволяющие оценить вызванные чисто случайными причинами допустимые расхождения между частотами в группах. Эти таблицы рассчитаны при выполнении нулевой гипотезы однородности и соответствуют ситуациям, когда частоты близки к 50% (табл.3.10) или к 20% (табл.3.11). Если наблюдаемые частоты - от 30 до 70%, то рекомендуется пользоваться первой из этих таблиц, если от 10 до 30% или от 70 до 90% - то второй. Если наблюдаемые частоты меньше 10 или больше 90%, то теорема Муавра-Лапласа и основанные на ней асимптотические формулы дают не очень хорошие приближения, целесообразно применять иные, более продвинутые математические средства, в частности, приближения с помощью распределения Пуассона.
| Объемы групп | 750 | 600 | 400 | 200 | 100 |
|---|---|---|---|---|---|
| 750 | 6 | 7 | 7 | 10 | 12 |
| 600 | 7 | 8 | 8 | 11 | 13 |
| 400 | 7 | 8 | 10 | 11 | 14 |
| 200 | 10 | 11 | 11 | 13 | 16 |
| 100 | 12 | 13 | 14 | 16 | 18 |
| Объемы групп | 750 | 600 | 400 | 200 | 100 |
|---|---|---|---|---|---|
| 750 | 5 | 5 | 6 | 8 | 10 |
| 600 | 5 | 6 | 7 | 8 | 10 |
| 400 | 6 | 7 | 8 | 9 | 11 |
| 200 | 8 | 8 | 9 | 10 | 12 |
| 100 | 10 | 10 | 11 | 12 | 14 |
В условиях разобранного выше примера табл.3.10 дает допустимое расхождение 7%. Действительно, объем первой группы 500 отсутствует в таблице, но строки, соответствующие объемам 400 и 600, совпадают для первых двух столбцов слева. Эти столбцы соответствуют объемам второй группы 750 и 600, между которыми расположен объем 700, данный в примере. Он ближе к 750, поэтому берем величину расхождения, стоящую на пересечении первого столбца и второй (и третьей) строк, т.е. 7%. Поскольку реальное расхождение (10%) больше, чем 7%, то делаем вывод о наличии значимого различия между группами. Естественно, этот вывод совпадает с полученным ранее расчетным путем.
Как и в табл. 3.5, значения в табл.3.10 и 3.11 несколько больше, чем рассчитанные по приведенным выше формулам. Как и раньше, дело в том, что таблицы ВЦИОМ связаны не с уровнем значимости  а с уровнем значимости
а с уровнем значимости 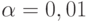 которому соответствует граничное значение 2,58.
которому соответствует граничное значение 2,58.
Допустимое расхождение  между частотами нетрудно получить расчетным путем. Для этого достаточно воспользоваться формулой для статистики
между частотами нетрудно получить расчетным путем. Для этого достаточно воспользоваться формулой для статистики  и определить, при каком максимальном расхождении частот все еще делается вывод о том, что верна гипотеза однородности. Следовательно, допустимое расхождение
и определить, при каком максимальном расхождении частот все еще делается вывод о том, что верна гипотеза однородности. Следовательно, допустимое расхождение  находится из уравнения
находится из уравнения

Таким образом,

Для данных примера 2 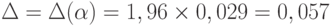 , или 5,7%, для уровня значимости 0,05.
, или 5,7%, для уровня значимости 0,05.
Для других уровней значимости надо использовать другие коэффициенты  . Так,
. Так, 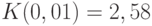 для уровня значимости 1% и
для уровня значимости 1% и 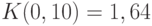 для уровня значимости 10%. Для данных примера
для уровня значимости 10%. Для данных примера 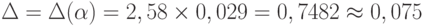 , или 7,5%, для уровня значимости 0,01. Если округлить до ближайшего целого числа процентов, то получим 7%, как при использовании табл. 7 выше.
, или 7,5%, для уровня значимости 0,01. Если округлить до ближайшего целого числа процентов, то получим 7%, как при использовании табл. 7 выше.
Анализ табл. 3.10 и 3.11 показывает, что для констатации различия частоты должны отличаться не менее чем на 6%, а при некоторых объемах выборок - более чем на 10%, при объемах выборок 100 и 100 - на 19%. Если частоты отличаются на 5% или менее, можно сразу сказать, что статистический анализ приведет к выводу о том, что различие не обнаружено (для выборок объемом не более 750).
В связи с этим возникает вопрос: каково типовое отличие частот в двух выборках из одной и той же совокупности? Разность частот в этом случае имеет нулевое математическое ожидание и дисперсию
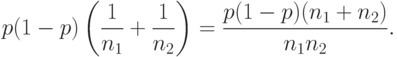
Величина  достигает максимума при
достигает максимума при 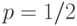 , и этот максимум равен 1/4. Если
, и этот максимум равен 1/4. Если 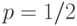 , а объемы двух выборок совпадают и равны 500, то дисперсия разности частот равна
, а объемы двух выборок совпадают и равны 500, то дисперсия разности частот равна

Следовательно, среднее квадратическое отклонение  равно 0,032, или 3,2%. Поскольку для стандартной нормальной случайной величины в 50% случаев ее значение не превосходит по модулю 0,67 (а в 50% случаев - больше 0,67), то типовой разброс равен
равно 0,032, или 3,2%. Поскольку для стандартной нормальной случайной величины в 50% случаев ее значение не превосходит по модулю 0,67 (а в 50% случаев - больше 0,67), то типовой разброс равен  , а в рассматриваемом случае - 2,1%. Приведенные соображения дают возможность построить метод контроля за правильностью проведения повторных опросов. Если частоты излишне устойчивы, значения при повторных опросах слишком близки - это подозрительно! Возможно, нарушены правила проведения опросов, выборки не являются случайными, и т.д.
, а в рассматриваемом случае - 2,1%. Приведенные соображения дают возможность построить метод контроля за правильностью проведения повторных опросов. Если частоты излишне устойчивы, значения при повторных опросах слишком близки - это подозрительно! Возможно, нарушены правила проведения опросов, выборки не являются случайными, и т.д.
Контрольные вопросы и задачи
- Почему выборочные исследования необходимы для решения многих практических задач?
- Рассчитайте коэффициент ценовой эластичности спроса по данным табл.1 при цене р = 35 и при цене р = 40.
- Какова роль теоремы Муавра-Лапласа в теории выборочных исследований?
В задачах 4 - 7 выберите наиболее подходящий вариант ответа.
- При какой цене максимальна прибыль в условиях параграфа 3.1, если издержки (оптовая цена книги) равны 12?
А) 30; Б) 32; В) 35.
- При исследовании предпочтений потребителей открытые вопросы:
А) труднее для опрашиваемых, но легче для обработки;
Б) легче для опрашиваемых, но труднее для обработки.
- Пусть из 657 опрошенных 289 сказали "да". Доверительный интервал для доли отвечающих "да" в генеральной совокупности, соответствующий доверительной вероятности 0,95, таков:
А) [0,245; 0,398]; Б) [0,435; 0,445]; В) [0,405; 0,556];
Г) [0,402; 0,478]; Д) [0,247; 0,633].
- Из 513 юношей 193 любят "Сникерс", а из 748 девушек - 327. Значение статистического критерия
 для проверки гипотезы о равенстве вероятностей равно:
для проверки гипотезы о равенстве вероятностей равно:А) 3,38; Б) -2,176; В) 0,25; Г) 12,56; Д) -0,173.
Гипотеза об одинаковой привлекательности "Сникерса" для юношей и девушек (на уровне значимости 0,05):А) принимается; Б) отклоняется.
- Как понятие допустимого расхождения между частотами можно использовать при планировании выборочных исследований?
Темы докладов, рефератов, исследовательских работ
- Проведите выборочное исследование с целью построения оценки функции ожидаемого спроса на выбранный Вами товар (услугу).
- Найдите адекватное приближение функции спроса в табл.1 с помощью метода наименьших квадратов.
- Постройте экономико-математическую модель оптимизации цены при заданных функциях спроса (в зависимости о цены) и издержек (в зависимости от выпуска).
- Сопоставьте теорию квотной выборки с теорией простой случайной выборки.
- Рассмотрите статистическую теорию доверительного оценивания и проверки гипотез о равенстве вероятностей ответов в случае нескольких возможных ответов (с использованием мультиномиального распределения вместо биномиального).
- В каких случаях может быть использована теория малых выборок (теорема Пуассона) для доверительного оценивания вероятности определенного ответа?
