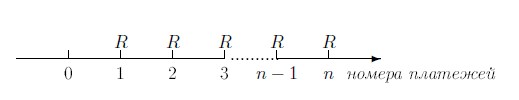НОУ ИНТУИТ | Элементы финансовой математики. Лекция 7: Приведенная ценность финансовой ренты

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.09.2017 | Доступ: свободный | Студентов: 1239 / 371 | Длительность: 12:18:00

Тема: Менеджмент

Специальности: Менеджер, Руководитель, Экономист

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В лекциях 2 и 5 уже рассматривался вопрос о приведённой ценности денежного потока. Такая же задача может быть поставлена и относительно финансовой ренты. Например, желая создать фонд для выплаты именных стипендий, основатель фонда должен знать, какую сумму необходимо вложить в этот фонд при его создании. Эта сумма равна приведённой ценности финансовой ренты, которую составляют выплаты стипендий. Приведённой ценностью ренты будем называть приведённую ценность её наращенной суммы.

Ключевые слова: ПО, значение, функция, фирма, стоимость

7.1 Функция для коэффицентов приведенной ценности финансовой ренты

Рассмотрим ренту, состоящую из n платежей, каждый из которых равен R и делается в конце каждого периода начисления процентов. Если за каждый период начисляются сложные проценты по ставке i, то наращенная сумма s этой финансовой ренты (см. лекция 6), вычисляется по формуле

$S=Rs_{n;\,i}.$

Приведённая ценность финансовой ренты равна приведённой ценности её наращенной суммы, следовательно, она вычисляется по формуле:

$PV = S(1+i)^{-n}=R\,s_{n;\,i}(1+i)^{-n}=R\,\frac{(1+i)^{n}-1}{i}(1+i)^{-n}=\\[2pt] = R\,\frac{1-(1+i)^{-n}}{i}$

Применяя обозначение PV для приведённой ценности денег в момент 0, будем обозначать приведённую ценность ренты, состоящей из n членов, равных R, через PV(R,n), а если из контекста значения R и n ясны, то - PV.

В финансовых вычислениях для величины, на которую умножается R в последней формуле, принято использовать следующее обозначение:

$a_{n;\,i}=\frac{1-(1+i)^{-n}}{i}\,\,\, (7.1)$

Тогда приведённая ценность ренты, состоящей из n периодических платежей, равных R каждый, на которые начисляются сложные проценты по ставке i за каждый период, выразится формулой:

$PV(R,n)=PV=Ra_{n;\,i}\,\,\, (7.2)$

Из формулы (60) видно, что значение функции 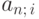$a_{n;\,i}$ - это приведённая ценность финансовой ренты, состоящей из n платежей, равных 1. Раньше для выполнения вычислений, использующих функцию 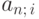$a_{n;\,i}$ , применялись специальные таблицы этой функции для различных значений n и i. 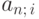Как и в случае с функцией $s_{n;\,i}$ , мы рекомендуем при решении примеров и упражнений, когда необходимо вычислить значение функции $a_{n;\,i}$ , использовать финансовый калькулятор или программу Excel. Заметим, что функция 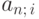$a_{n;\,i}$ не входит в число встроенных финансовых функций Excel. Но это легко исправить, так как нетрудно написать свою функцию, выполняющую вычисления по формуле (7.1), на VBA.

Покажем, что формулу (7.2) можно вывести другим способом. Изобразим ренту, состоящую из n платежей, на оси времени:

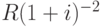Ценность первого платежа в момент 0 равна $R(1+i)^{-1}$ ; ценность второго платежа в момент 0 равна $R(1+i)^{-2}$ и т.\,д.; ценность n-го, последнего платежа, в момент 0 равна 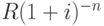$R(1+i)^{-n}$ . Суммарная ценность всех платежей в момент 0 (приведённая ценность ренты) равна:

$PV(R,n)=R(1+i)^{-1}+R(1+i)^{-2}+\ldots+R(1+i)^{-n}.$

Теперь применим формулу суммы первых n членов геометрической прогрессии с первым членом $b_{1}=R(1+i)^{-1}$ и знаменателем $q=(1+i)^{-1}$ . Выполнив приведённые ниже преобразования, получим формулу (7.2):

$PV(R,n) = \frac{b_{1}(q^{n}-1)}{q-1}=\frac{R(1+i)^{-1}[(1+i)^{-n}-1]}{(1+i)^{-1}-1}=\\[6pt] = \frac{R(1+i)^{-1}[(1+i)^{-n}-1]}{\displaystyle{{\frac{1-(1+i)}{1+i}}}}= R\frac{1-(1+i)^{-n}}{i}=Ra_{n;\,i}.$

Дальше >>

Авторизоваться

Элементы финансовой математики

Приведенная ценность финансовой ренты

7.1 Функция для коэффицентов приведенной ценности финансовой ренты

Вопросы и ответы