Приведенная ценность финансовой ренты

7.2 Как обеспечить получение ренты в будущем

Покажем, что с помощью формулы (7.2) можно решать задачи следующего содержания: какую сумму надо вложить в определённый момент времени под i%, чтобы иметь возможность получать сумму R в конце каждого из n следующих периодов начисления процентов?

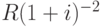Не умаляя общности, можно считать, что определяемая сумма s размещается на счёте в момент 0. Запишем необходимые условия получения требуемых платежей. Чтобы получить в момент 1 сумму R, необходимо вложить в момент 0 сумму . Чтобы получить в момент 2 сумму R, необходимо вложить в момент 0 сумму и т.д. Чтобы получить в момент n сумму R, необходимо вложить в момент 0 сумму 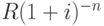. Эти величины совпадают с полученными в п. 7.1. Следовательно, суммируя их, как и там, получим формулу (7.2). Но теперь эта формула выражает сумму, которую надо вложить в момент 0, чтобы получить в конце следующих периодов n платежей, равных R каждый.

Пример 62. Фирма собирается оплатить получение высшего образования своему сотруднику. Продолжительность обучения 5 лет, стоимость - 250 000 руб. за один учебный год (деньги вносятся в начале учебного года). За год до начала учёбы фирма открывает счёт в банке, который будет начислять на этот счёт проценты по ставке 7% годовых (сложных). Какую сумму необходимо положить на счёт при открытии, чтобы имеющихся на счёте денег хватило на оплату учёбы в течение пяти лет?

Решение.Необходимая сумма равна ценности в момент 0 ренты, состоящей из пяти платежей по 250 000 руб. каждый, при i=7%=0.07. По формуле (7.2) имеем:

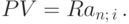
Любым из предложенных выше способов можно вычислить, что 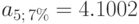. Подставив найденное значение в формулу, получаем ответ:

Заметим, что найденная сумма является минимально необходимой для оплаты учёбы. Если в начальный момент на счёт будет положена именно такая сумма (1 025 049 руб.), то денег хватит на оплату обучения и на счёте не останется денег после последней (пятой) уплаты.

7.3 Приведённая ценность различных рент

Рассмотрим теперь приведённую ценность некоторых типов финансовых рент при различных способах начисления процентов: в конце года, m раз в год, непрерывном. В лекции не рассматриваются ренты с периодом больше года, редко встречающиеся на практике.

7.3.1 Ренты с начислением процентов в конце года

Годовая рента

Приведённая ценность этой ренты определяется по формуле (7.2), где n - число лет, i - годовая ставка сложных процентов.

-срочная рента

Используя формулы из формулы из лекций 3 и 6, находим современную ценность PV этой ренты:

Введем обозначение:

Тогда формула для PV принимает вид:

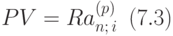
Коэффициент 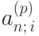можно представить в виде произведения:

то есть верна формула:

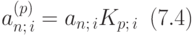
где 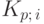- обозначение, которое уже использовалось в лекции 6 для правого множителя в предыдущей формуле.