Принцип отсутствия арбитражных возможностей

9.1 Финансовый арбитраж

Финансовым арбитражем^{1Арбитраж - от фр. arbitrage}называется особый вид коммерческой деятельности, направленный на извлечение прибыли из разницы цен одинаковых (или родственных) биржевых активов при нарушении между их ценами паритетных отношений. Людей, которые профессионально занимаются арбитражными операциями, называют арбитражёрами. Начнём с простейших примеров.

Пример 78. В рассматриваемый день акция компании А стоила на бирже в городе N 225.75 руб., а в городе M - 231.72 руб. Арбитражёр купил 1 000 акций компании А в городе N и продал их в городе M. Вычислим доход арбитражёра, если биржа в городе N удерживает 0.1% от суммы сделки, а в городе M - 0.2%.

Решение.Арбитражёр потратил на покупку акций в городе N с учётом комиссии

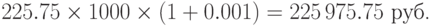
и получил при продаже в городе M с учётом комиссии

Следовательно, доход арбитражёра равен

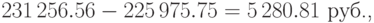
что в процентах от затраченной суммы составляет 2.34%

Выше приведен пример простейшего арбитража. Более сложный, но и более актуальный пример мы получим при перекрестном валютном арбитраже.

Пример 79. В рассматриваемый момент времени на валютной бирже в городе N доллар стоил 63.05 руб., а евро - 70.35 руб. В тот же момент на бирже в городе M за один евро давали 1.25 доллара. Брокер из города N имеет возможность совершать сделки на обеих площадках. Сделку в городе N можно произвести без удержания комиссионных, а при сделке в городе M перевод валюты в город N стоит 0.1% от суммы сделки. Проанализируем арбитражные возможности брокера.

Решение.Покажем, что брокер может получить доход, проведя следующую операцию: купить евро в N за рубли; продать евро и получить доллары в M; перевести полученные доллары в N и продать их, получив рубли. Для определённости предполагаем, что на первом шаге (в городе N) была куплена 1 000 евро. На покупку евро брокер потратил сумму, равную 70 350 руб. Далее эти евро будут потрачены на покупку долларов в M. Учтем, что при переводе удерживается 0.1% от суммы:

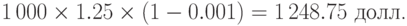
Далее, продав полученные в N, брокер получит сумму, равную

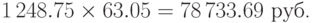
Следовательно, доход брокера равен

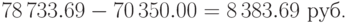
Выразим величину дохода в процентах:

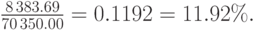
Арбитражные возможности, типа описанных в примере \ref{ex:a2n}, быстро исчезают в результате активности трейдеров. Другой пример арбитража мы получим при анализе процентно-валютного паритета.

Пример 80. Предположим, что в первой стране (A) годовая ставка процента по безрисковым ценным бумагам равна 8%, а во второй (B) - 6%. Обменный курс равен 1.8 единиц валюты страны B за 1 единицу валюты страны A. Предполагается, что к концу года этот курс составит 1.5. Проанализируем арбитражные возможности при покупке безрисковых ценных бумаг.

Решение. Для удобства будем писать после сумм в валютах стран A и B символы A и B соответственно. Если купить безрисковые ценные бумаги в стране B, то, вложив 1 B в начале года, мы получим 1.06 B в конце года. Если перевести 1 B в валюту A, то мы получим 1/1.8=0.56 A, вложив которые в ценные бумаги страны A мы получим:

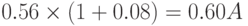
Переводя эту сумму в валюту B в конце года, получаем сумму 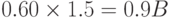, что меньше, чем 1.06 B. Это связано с тем, что более высокая ставка в стране A была перевешена ожидаемым спадом обменного курса ее валюты. В данном случае арбитражеры будут покупать ценные бумаги страны B. Легко вычислить, что паритету, после которого арбитражеры начнут переводить валюту B в валюту A и вкладывать в ценные бумаги с более высокой ставкой доходности, соответствует обменный курс ex валюты A на валюту B, удовлетворяющий уравнению:

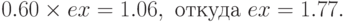
Следовательно, арбитражеры начнут переводить валюту B в валюту A и покупать ценные бумаги страны A, если обменный курс будет не менее 1.77 B за 1 A.

Важно отметить, что арбитражные возможности рассмотренных типов не могут быть долговременными. Цены одинаковых объектов на разных биржах в результате арбитражных операций выравниваются, поэтому цены активов в будущем рассчитываются так, чтобы арбитражная операция была невозможна. Модели финансовых операций с ценными бумагами и другими инструментами строятся на принципе отсутствия арбитража. Более того, принцип отсутствия арбитража является основным принципом ценообразования на финансовые активы.

Пример 78 относился к простейшему виду арбитража - пространственному арбитражу. В примере 80 уже присутствовали неопределённость и время. Напомним, что один и тот же актив, рассматриваемый в разные моменты времени, является родственным себе, но не идентичным себе активом - его ценность и цена могут измениться.

Далее в этой лекции мы рассмотрим применения принципа отсутствия арбитражных возможностей к ценообразованию на срочные контракты.