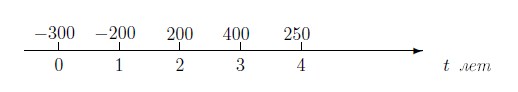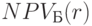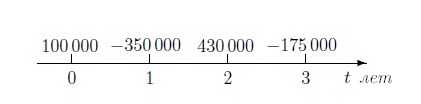Анализ инвестиционных проектов
10.1 Инвестиционные проекты
Инвестиционный проект - это долгосрочный календарный план вложения средств инвестора в такие активы, как оборудование, здания, земля, технологии и т.п., с целью получения доходов от этих вложений.
Предполагается, что инвестор имеет одну или несколько возможностей инвестиций, которые заслуживают внимания. Предполагается также, что уже проведен необходимый анализ, который позволяет указать точные суммы затрат и доходов на каждом интервале времени в будущем для этих проектов. Это означает, что мы ограничиваемся рассмотрением инвестиционных проектов в условиях полной определённости. При анализе инвестиций - это основной, базисный случай. Учёт неопределённости на практике необычайно важен - он ужесточает требования к доходности проекта. Но этот материал не будет освещён в нашем вводном курсе лекций.
В каждом периоде времени инвестиционный проект предполагает как доходы, так и затраты. Доходы состоят из выручки от реализации продукции и услуг, связанных с данным проектом. Затраты можно разделить на капиталовложения - инвестиции (покупка оборудования, патентов и т.п.) и текущие затраты (стоимость полуфабрикатов, сырья и комплектующих, оплата труда, рентные платежи и т.п.). Часто доходы называют притоком денежных средств, а затраты - оттоком. Мы далее будем использовать эти термины.
Инвестиционный проект порождает поток денежных средств, каждый элемент которого равен разности между притоком и оттоком денежных средств. Эти суммы принято называть платежами. На оси времени инвестиционный проект можно изобразить так:
Здесь  числа, равные величине потока денежных средств в соответствующие интервалы времени. Числа
числа, равные величине потока денежных средств в соответствующие интервалы времени. Числа 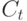 могут быть любого знака. Если речь идет о проекте типа строительства нового предприятия, то несколько первых лет инвестиции будут превосходить доходы от производства (которые обычно возникают не с первого года). В этом случае
могут быть любого знака. Если речь идет о проекте типа строительства нового предприятия, то несколько первых лет инвестиции будут превосходить доходы от производства (которые обычно возникают не с первого года). В этом случае 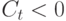 . При выходе производства на регулярный график величина
. При выходе производства на регулярный график величина 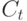 равна чистой прибыли за период, поэтому в плане она, как правило, положительна:
равна чистой прибыли за период, поэтому в плане она, как правило, положительна:  . Тот факт, что в реальном производстве бывают провалы и случается, что прибыль за период (квартал, год) отрицательна, не может быть элементом планирования. Такого рода эффекты оцениваются с помощью анализа проектов в условиях неопределённости, что, как мы уже говорили, выходит за рамки нашего курса лекций.
. Тот факт, что в реальном производстве бывают провалы и случается, что прибыль за период (квартал, год) отрицательна, не может быть элементом планирования. Такого рода эффекты оцениваются с помощью анализа проектов в условиях неопределённости, что, как мы уже говорили, выходит за рамки нашего курса лекций.
В практике финансовой деятельности инвестиционные расчёты, как правило, выполняются за промежуток времени, равный (финансовому) году. Поэтому моменты времени  в дальнейшем примем равными
в дальнейшем примем равными  годам соответственно, а поток платежей, порождённый инвестиционным проектом, будем изображать так:
годам соответственно, а поток платежей, порождённый инвестиционным проектом, будем изображать так:
Инвестиционный проект будем называть регулярным, если в последовательности чисел 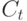 происходит не более одной смены знака. Это означает, что знаки чисел C_t образуют последовательности типа:
происходит не более одной смены знака. Это означает, что знаки чисел C_t образуют последовательности типа:

Приведём пример регулярного инвестиционного проекта.
Пример 87. Фирма анализирует проект производства нового вида продукции. В начальный момент времени потребуется 300 тыс. руб. на анализ рынка и закупку необходимого оборудования. В первый год на запуск производства и рекламную кампанию потребуется 200 тыс. руб. Во второй, третий и четвертые годы реализация новой продукции принесет доход в размере 200 тыс. руб., 400 тыс. руб. и 250 тыс. руб. соответственно. Предполагается, что в пятом году данный вид продукции устареет и её дальнейший выпуск станет нецелесообразным. Изобразим этот проект на оси времени и на диаграмме.
Решение. На оси времени данный проект может быть изображен так (числа над осью обозначают тысячи рублей):
Диаграмма этого же проекта приведена на рис. 25. Как построить эту диаграмму в Excel, будет объяснено в этой лекции далее.
Бывают и нерегулярные инвестиционные проекты, когда после нескольких притоков денежных средств снова производятся инвестиции, то есть происходят оттоки денежных средств. не используется Таким может быть, например, проект производства новой модели автомобиля: сначала закупается и начинает работать первая линия сборки; от неё начинают поступать доходы; затем закупается более мощная, вторая линия сборки, поэтому в этот период отток денежных средств превышает их приток; далее, когда начинают в полную силу работать обе линии сборки, приток денежных средств существенно увеличивается.
Если с некоторого момента инвестиции в проект постоянно превосходят доходы (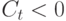 ), то такой проект, как правило, не может быть принят. Реализацию таких проектов может позволить себе только государство в целях развития науки, обороны, социального обеспечения и тому подобного.
), то такой проект, как правило, не может быть принят. Реализацию таких проектов может позволить себе только государство в целях развития науки, обороны, социального обеспечения и тому подобного.
Для оценки инвестиционных проектов применяются разные критерии. Каждый из них даёт определённую информацию к размышлению, позволяет выбрать тот или иной из альтернативных проектов. Далее мы рассмотрим различные критерии оценки инвестиционных проектов. Но начнём мы с самого важного критерия - чистой приведённой ценности инвестиционного проекта (NPV).
10.2 Метод чистой приведённой ценности
Инвестиционный проект ассоциируется с потоком платежей:

в годы  . При этом знак
. При этом знак 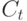 может быть как положительным, так и отрицательным.
может быть как положительным, так и отрицательным.
В простейшем случае можно отождествлять  с начальным капиталовложением I , то есть
с начальным капиталовложением I , то есть  , а
, а 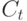 при
при  считать чистым доходом, связанным с этим проектом.
считать чистым доходом, связанным с этим проектом.
Каждый член потока платежей, порождённого инвестиционным проектом, имеет свою приведённую ценность в момент 0. Учитывая взаимосвязь этих платежей, важной характеристикой проекта является сумма приведённых ценностей в момент 0 всех членов денежного потока, начиная с 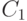 , которую называют приведённой ценностью инвестиционного проекта:
, которую называют приведённой ценностью инвестиционного проекта:

где r - ставка дисконтирования (discount rate).
Заметим, что в некоторой финансовой литературе величину PV называют по-другому: приведённая величина, современная стоимость и капитализированная стоимость. Важно понимать, что каждый раз речь идёт о величине, которая вычисляется по формуле (97).
В том случае, когда учитывают и вложения  в момент 0, говорят
о чистой приведённой ценности инвестиционного проекта:
в момент 0, говорят
о чистой приведённой ценности инвестиционного проекта:

Чистую приведённую ценность принято обозначать аббревиатурой NPV (от английского Net Present Value.
В качестве ставки дисконтирования r может быть принята безрисковая ставка процента или ставка прибыли для проектов той же степени риска, или средняя отраслевая норма доходности. Иногда за ставку дисконтирования принимается необходимая с точки зрения фирмы норма прибыли.
Если NPV проекта отрицательна, то принимать такой проект не имеет смысла. Из нескольких альтернативных проектов следует принять тот, который имеет более высокую NPV при одной и той же ставке дисконтирования.
Пример 88. Найдем NPV инвестиционного проекта из примера 87, если ставка дисконтирования 
Решение. По формуле (98) получаем (округляя до тыс. руб.):

Величина чистой приведённой ценности проекта зависит от ставки дисконтирования, то есть NPV есть функция r. Следующий пример иллюстрирует зависимость NPV от r.
Пример 89. Построим график функции NPV(r) инвестиционного проекта, описанного в примере 87.
Решение. Вычислим по формуле (98) значения функции NPV(r) , округляя до тыс. руб., при r=0%, 20%, 30%, 40%. Результаты вычислений запишем в таблицу:
График функции NPV(r) , построенный в Excel по найденным точкам, приведён на рис. 26.
Легко показать, что функция NPV(r) инвестиционного проекта, у которого  , является убывающей функцией. Действительно, если ставка дисконтирования r увеличивается, то множитель
, является убывающей функцией. Действительно, если ставка дисконтирования r увеличивается, то множитель 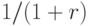 уменьшается.
уменьшается.
В примере 89 при ставке дисконтирования r=20% проект имеет положительную NPV и его можно принять, а при ставке дисконтирования  и проект следует отклонить. Подобная зависимость рекомендации от незначительного изменения ставки дисконтирования, правильное значение которой никто не знает, снижает практические достоинства метода NPV Чтобы применение этого метода было оправдано, надо очень тщательно выбирать ставку дисконтирования.
и проект следует отклонить. Подобная зависимость рекомендации от незначительного изменения ставки дисконтирования, правильное значение которой никто не знает, снижает практические достоинства метода NPV Чтобы применение этого метода было оправдано, надо очень тщательно выбирать ставку дисконтирования.
Необходимо понимать, что при сравнении двух (и более) проектов по критерию NPV можно прийти к разным выводам при различных ставках дисконтирования. Рассмотрим пример.
Пример 90. Наряду с проектом, описанным в примере 87 (будем называть его проект А), компания рассматривает проект Б выпуска другого вида продукции. Первоначальные вложения по обоим проектам совпадают 300 тыс.руб.). Проект Б требует больших инвестиций в первом году~- 300 тыс.руб. Ожидаемые доходы по проекту Б составят: 100 тыс.руб.\ во второй год, 600 тыс.руб.\ в третий год и 300 тыс.руб. в четвертом году. Построим график функции NPV(r) этих проектов и сравним их по критерию NPV при различных значениях ставки дисконтирования r.
Решение. По формуле (98) вычислим значения функции NPV(r) обоих проектов при различных значениях r . Результаты вычислений приведены в следующей таблице:
Графики функций NPV(r) обоих проектов, построенные по найденным точкам, приведены на рис.27. Эти графики пересекаются в точке с абсциссой, приблизительно равной 14%.
Таким образом, если NPV этих проектов вычислены при ставке дисконтирования, меньшей 14% например при r=10%, то следует предпочесть проект Б, так как NPV проекта Б при этой ставке дисконтирования больше, чем NPV проекта А:

Если же NPV этих проектов вычислены при ставке дисконтирования, большей 14%, например при r=20%, то следует предпочесть проект А, так как NPV проекта А при этой ставке дисконтирования больше, чем у проекта Б:

Если инвестиционный проект не является регулярным, то функция NPV(r) может быть произвольного вида. Приведём пример.
Пример 91. В момент 0 инвестор берет кредит в банке в размере 100 00руб. Используя эти деньги в биржевых операциях, в течение первого года он зарабатывает 350 00 руб, которые инвестирует в проект. К концу второго года инвестор получит 430 00руб. дохода, а в третьем году понесет 175 000 руб.\ убытка. Построим график функции NPV(r) этого проекта.
Решение. Изобразим проект на оси времени:
Функция NPV(r) рассматриваемого проекта имеет вид:

Найдем несколько значений функции NPV(r) и построим график (рис. 28):