Процентные вычисления

Цель лекции: научиться распознавать и решать четыре типа задач на процентные вычисления; ознакомиться с основными методами ценообразования; решать разобранные типы задач в Excel.

1.1 Понятие процента

Процентом некоторой величины называется сотая доля этой величины. Такой величиной может быть месячный доход семьи, годовая прибыль фирмы, сумма государственного бюджета. Чтобы указать, что величина выражена в процентах, используется специальное обозначение:%. Термин "процент" произошёл от латинского pro centum - на сотню, или за сто. Выражать доли величин в процентах принято в финансовых и статистических расчётах, а также во многих других областях.

В дореволюционной России процент, получаемый за сумму, данную в долг или инвестируемую в некоторое предприятие, в купеческой среде называли интересом.

Гораздо реже используется специальное обозначение для тысячной доли целого (или десятой доли процента) - промилле. Термин "промилле" произошёл от латинского pro mille - на тысячу, или за тысячу. Для промилле также имеется специальное обозначение: %. В страховом деле плату за страхование (страховую премию) удобно, порой, выражать не в процентах, а в промиллях. Например, если имущество застраховано на 100 000 руб. c 3%, то страховая премия составляет

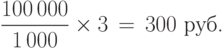
Необходимо различать два понимания термина процент. Во-первых, процент выступает как процентное число, указывая на часть целой величины или долю. Именно такое понятие процента чаще всего используется в социально-экономической статистике и законодательной практике регулирования предпринимательской деятельности. Например, в 2013 г. доходы от налога на прибыль предприятий составили 3.46% в общей сумме доходов Федерального бюджета Российской Федерации (12 865.9 млрд рублей). Примером законодательных формулировок, в которых используются процентные числа, являются нормы, определяющие налог на добавленную стоимость (НДС) в размере 18% или налог на прибыль корпораций в размере 20%. Однако эти величины часто меняются законодателем, поэтому читатель должен ориентироваться на современные правовые акты.

Во-вторых, и это основное понимание процента в этом курсе, процент связан с начислением сумм (процентных платежей) за определённые промежутки времени. При этом здесь следует различать ставку процента (interest rate) как некоторое число, выраженное в процентах или долях (единицы) данной величины и проценты (interest) как соответствующее абсолютное количество данной величины. Например, при годовой ставке 10% по вкладу в банке, что есть указание на годовую процентную ставку по вкладу, и начальной величине вклада 100 000 руб. наращенная за год сумма 10 000 руб. называется процентами по вкладу.

Важное замечание. Если в тексте написано r%, то эта величина равна вещественному числу r/100: 10%=0.1. И наоборот, если в тексте написано вещественное значение (без знака %), то ему соответствует i*100%: 0.1=10%.

В настоящей лекции мы рассмотрим лишь простейшие задачи на процентные вычисления, связанные с первым пониманием процента как процентного числа. Внимание - и здесь можно ошибиться!

При процентных вычислениях очень важно отчётливо понимать, какая величина принята за 100%. Эта величина называется базой. Например, в упомянутом выше примере с Федеральным бюджетом Российской Федерации базой является сумма бюджета в 12 865.9 млрд, рублей. Тогда 3.46% налоговых поступлений означают, что величина налоговых поступлений составила

Рассмотрим четыре задачи на процентные числа, на которые мы затем в будем ссылаться как на четыре основные задачи.

Основная задача 1. Определить число, которое составляет n% от числа A.

Решение. Обозначим искомое число через x и запишем условия задачи в следующем виде:

Эту запись иногда называют процентной пропорцией, которая может быть записана так:

откуда получаем формулу для вычисления значения числа x:

Основная задача 2. Определить число, n% которого равны B.

Решение. Обозначим искомое число через x и запишем условия задачи в следующем виде:

Имеет место следующая пропорция:

откуда получаем формулу для вычисления значения числа x:

Основная задача 3. Определить, сколько процентов от числа A составляет число B.

Решение. Обозначим искомое число процентов через x и запишем условия задачи следующем виде:

Имеет место следующая пропорция:

откуда получаем формулу для вычисления значения числа x:

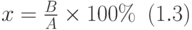
Основная задача 4. Определить, сколько процентов от некоторого числа составляет число B, если n% этого числа равны A.

Решение. Обозначим искомое число процентов через x и запишем условия задачи следующем виде:

Имеет место следующая пропорция:

откуда получаем формулу для вычисления значения x:

Заметим, что формула 1.3 является частным случаем формулы 1.4, а основная задача 3 - частным случаем основной задачи 4 при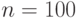

Решение любых примеров на процентные числа базируется на решении этих четырёх основных задач.