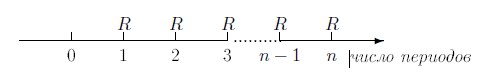Финансовые ренты
6.1 Основные определения
Финансовой рентой называется последовательность платежей, равных по величине и производящихся через равные промежутки времени.
Временной интервал между последовательными выплатами называется периодом ренты. Чаще всего встречаются ренты, период которых равен году, половине года, кварталу или месяцу. Срок от начала первого до конца последнего периода называется сроком ренты. Если последний период не указывается (срок ренты бесконечный), то рента называется бессрочной.
Ренты бывают условные и безусловные. Безусловная рента имеет фиксированный срок, а срок условной ренты зависит от наступления некоторого события. Платежи по ипотеке или потребительскому кредиту являются безусловной рентой, а пенсия - условной рентой. В этой лекции рассматриваются только безусловные ренты.
Если выплаты производятся в конце периода, то рента называется обычной или постнумерандо, если выплаты производятся в начале периода, то рента называется авансированной или пренумерандо.
6.2 Функция коэффициентов для финансовой ренты
При выводе формул, связанных с финансовыми рентами, мы будем неоднократно применять формулу суммы первых n членов геометрической прогрессии. Напомним, что геометрической прогрессией называется последовательность чисел 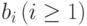 , в которой каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q, которое называется знаменателем прогрессии:
, в которой каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q, которое называется знаменателем прогрессии:
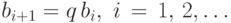
Сумма 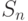 первых n членов геометрической прогрессии, у которой
первых n членов геометрической прогрессии, у которой  , вычисляется по формуле:
, вычисляется по формуле:

Рассмотрим обычную ренту, состоящую из n платежей, например, вкладов в банк. Обозначим через R величину рентного платежа. Предположим, что в конце каждого периода на все сделанные до этого момента платежи начисляются сложные проценты по ставке i. Изобразим такую ренту на оси времени:
Выведем формулу вычисления наращенной суммы рентных платежей к концу периода n, которую будем обозначать через S.
Платеж, сделанный в момент n, входит в наращенную сумму S без изменения, то есть в размере R. Сумма, наращенная к моменту n на платеж, сделанный в момент n-1, равна R(1+i) . Сумма, наращенная к моменту n на платеж, сделанный в момент n-2, равна 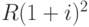 и т.д. Сумма, наращенная к моменту n на платеж, сделанный в момент 2, равна
и т.д. Сумма, наращенная к моменту n на платеж, сделанный в момент 2, равна 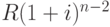 . Сумма, наращенная к моменту n на платеж, сделанный в момент 1, равна
. Сумма, наращенная к моменту n на платеж, сделанный в момент 1, равна 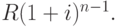
Следовательно, наращенная сумма всей ренты в момент n будет равна:
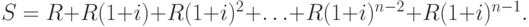
Слагаемые этой суммы являются членами геометрической прогрессии, первый член которой  , знаменатель q=1+i. По формуле (45) находим сумму первых n членов этой геометрической прогрессии:
, знаменатель q=1+i. По формуле (45) находим сумму первых n членов этой геометрической прогрессии:
![S=\frac{b_{1}(q^{n}-1)}{q-1}=\frac{R[(1+i)^{n}-1]}{1+i-1}=
R\,\frac{(1+i)^{n}-1}{i}\,.](/sites/default/files/tex_cache/f50022ff2fea3ad6cd682b9fceaa32f4.png)
Для коэффициента, на который умножается R в получившейся формуле, принято использовать следующее обозначение:
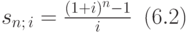
Тогда наращенная сумма финансовой ренты выражается формулой:

Из формулы (6.3) видно, что значение функции  - это наращенная за n периодов сумма финансовой ренты с платежами, равными 1. Ранее, когда компьютеры еще не были так распространены, для выполнения расчётов по формуле (использовались специальные таблицы значений функции
- это наращенная за n периодов сумма финансовой ренты с платежами, равными 1. Ранее, когда компьютеры еще не были так распространены, для выполнения расчётов по формуле (использовались специальные таблицы значений функции  . Теперь для вычисления значений этой функции можно использовать финансовый калькулятор или программу Excel. Заметим, что функция
. Теперь для вычисления значений этой функции можно использовать финансовый калькулятор или программу Excel. Заметим, что функция  не входит в число встроенных финансовых функций Excel. Но это легко исправить, так как нетрудно написать свою функцию, выполняющую вычисления по формуле (46), на VBA.
не входит в число встроенных финансовых функций Excel. Но это легко исправить, так как нетрудно написать свою функцию, выполняющую вычисления по формуле (46), на VBA.
Рассмотрим два примера на применение формулы (6.3).
Пример 54. Фирма создаёт фонд помощи ветеранам труда, вкладывая ежегодно 250 000 руб. в банк, выплачивающий 8% годовых (сложных). Какая сумма будет на счёте фонда через 5 лет?
Решение. Вклады в банк образуют простую ренту (далее просто ренту), для которой R=250 000 руб., n=5, i=8%. Вычисляем наращенную сумму ренты по формуле(6.3), подставляя в нее 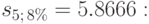
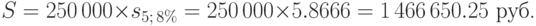
Пример 55. Предприниматель вкладывает 10 000 руб. в конце каждого месяца в банк, выплачивающий проценты по ставке 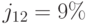 . Какую сумму он накопит за 2 года?
. Какую сумму он накопит за 2 года?
Решение. Вклады в банк, которые делает предприниматель, образуют финансовую ренту, в которой R=10 000, n=24, (2 года по 12 месяцев), i=0.09/12=0.0075. Находим наращенную сумму ренты по формуле (47), подставляя в неё 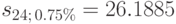
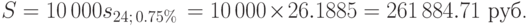
Сделаем важное замечание, касающееся авансированных рент, когда платежи делаются в начале периода. Наращенная сумма авансированной ренты выражается формулой:
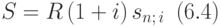
Действительно, вместе с авансированной рентой можно рассмотреть обычную ренту с тем же множеством платежей, которая начинается на один период раньше. Наращенные суммы этих рент в момент n должны совпадать, поэтому получаем формулу (6.4). Подобные несложные изменения потребуется выполнять и в остальных формулах, приведенных в этой лекции, если применять их для авансированных рент.