Операции с финансовыми контрактами
8.1 Эквивалентность контрактов
Рассмотрим сначала ситуацию, когда изменяются только сроки платежей. При этом возникает законный вопрос, как должны измениться суммы платежей. В данной ситуации это выражается с помощью двух простых формул.
Если срок платежа суммы  переносится на
переносится на  периодов вперед, то новая сумма платежа
периодов вперед, то новая сумма платежа  вычисляется по формуле:
вычисляется по формуле:
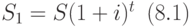
если срок платежа сокращается на  периодов, то новая сумма платежа
периодов, то новая сумма платежа  вычисляется по формуле:
вычисляется по формуле:
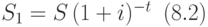
Последние две формулы можно объединить в одну, если заметить, что степень, в которую возводится множитель наращения 1+i, равна разности между новым и старым моментами платежа. Обозначим через t старый момент платежа, 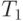 - новый момент платежа. Новая сумма платежа
- новый момент платежа. Новая сумма платежа  получается из старой s по формуле:
получается из старой s по формуле:
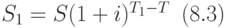
Рассмотрим пример, при решении которого применяется эта формула.
Пример 69. Предприниматель по договору должен выплатить банку 1 июля 2017 г. 120 000 руб. Банк даёт ссуды под 18% годовых (сложных). В договоре оговорена возможность как досрочного возврата ссуды, так и продления срока ссуды без изменения процента. Вычислим, какую сумму должен предприниматель вернуть в банк, если он решил вернуть долг: а) 1 января 2016 г.; б) 1 января 2018г.
Решение.
- а) Так как платеж делается на 1.5 года раньше срока, то предприниматель должен внести в банк меньшую сумму:

- б) В этом случае платеж делается на 0.5 года позже срока, поэтому в банк придется внести сумму, большую, чем 120 000 руб.:
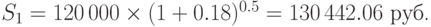
Рассмотрим теперь ситуацию объединения (консолидации) платежей: требуется заменить несколько платежей  со сроками выплат
со сроками выплат  соответственно, одним платежом
соответственно, одним платежом 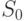 . При этом могут возникнуть две задачи: определить величину объединённого платежа
. При этом могут возникнуть две задачи: определить величину объединённого платежа 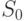 , если он должен быть сделан в момент времени
, если он должен быть сделан в момент времени  ; определить срок
; определить срок  платежа
платежа 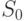 . Изобразим рассматриваемую ситуацию на оси времени:
. Изобразим рассматриваемую ситуацию на оси времени:
Для эквивалентности замены платежей необходимо, чтобы в момент 0 приведённая ценность платежа 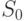 была равна сумме приведённых ценностей всех платежей
была равна сумме приведённых ценностей всех платежей 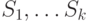 , то есть должно выполняться равенство:
, то есть должно выполняться равенство:
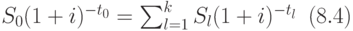
Если требуется определить величину единого платежа 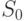 , то из последнего равенства получаем формулу:
, то из последнего равенства получаем формулу:
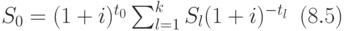
Чтобы определить срок  платежа
платежа 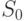 , решим уравнение (8.3) относительно
, решим уравнение (8.3) относительно  . Прологарифмируем обе части этого уравнения и, выполнив необходимые преобразования, получим формулу для
. Прологарифмируем обе части этого уравнения и, выполнив необходимые преобразования, получим формулу для  :
:
![\ln S_{0}(1+i)^{-t_{0}} = \ln\sum_{l=1}^{k}S_{l}(1+i)^{-t_{l}};\\[4pt]
\ln S_{0}-t_{0}\ln(1+i) = \ln\sum_{l=1}^{k}S_{l}(1+i)^{-t_{l}};
\\
t_{0}= {\ln
S_{0}-\ln\sum\limits_{l=1}^{k}S_{l}(1+i)^{-t_{l}}\over\ln(1+i)}\,\,\, (8.6)](/sites/default/files/tex_cache/6ddb9b1bae629bc730f791fc8a5078df.png)
Важно понимать, что на результат вычислений по формулам (8.5) и (8.6) не может повлиять то, в каких единицах выражены суммы платежей: в рублях, тысячах или миллионах рублей. Необходимо только соблюдать следующее правило: все платежи должны быть выражены в одних и тех же единицах.
Пример 70. По контракту предприниматель должен выплатить поставщику сырья через полгода после поставки 800 00 руб., ещё через полгода - 1 500 000 руб. и ещё через полгода - 1 300 000 руб. Эти платежи решено объединить в один платеж и выплатить весь долг через год после поставки сырья. Вычислим, какую сумму надо выплатить, если на долг начисляется 16% годовых (сложных).
Решение. Чтобы применить формулу (8.5), требуется сначала вычислить моменты платежей (единицей измерения является год): 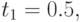 . Приводя все платежи к моменту времени 0, получаем по этой формуле:
. Приводя все платежи к моменту времени 0, получаем по этой формуле:
![S_0=(1+0.16)^{1}\times\left[\,800\,000(1+0.16)^{-0.5}+ \right.\\[6pt]
\left.+ 1\,500\,000(1+0.16)^{-1}+ 1\,300\,000(1+0.16)^{-1.5}\,\right]=\\[6pt]
= 3\,568\,646.07\mbox{ руб.}](/sites/default/files/tex_cache/db0358092caab6bc1d06d060090e54cb.png)
Пример 71. Предприниматель из предыдущего примера планирует выплатить долг одним платежом, равным 3 600 000 руб. Определим, в какой момент он должен сделать такой платеж.
Решение. Как было отмечено выше, результат вычислений не зависит от того, в каких единицах выражены суммы платежей. Воспользуемся этим свойством и выразим платежи из условия примера в миллионах рублей. По формуле (8.6) находим значение  :
:
![t_{0}={\ln 3.6 -\ln\left(0.8\times 1.16^{-0.5}+1.5\times 1.16^{-1}+1.3\times 1.16^{-1.5}\right)%
\over\ln 1.16}=\\[10pt]
=1.06\mbox{ года}=1\mbox{ год } 22\mbox{ дня.}](/sites/default/files/tex_cache/1910cc5ecb3d27cb2fda20219b294165.png)
Следовательно, суммы 3.6 млн руб. хватит, чтобы погасить долг не позднее чем через 1 год 22 дня после поставки сырья.

