Процентные вычисления

1.2 Примеры задач на процентные числа

Пример 1. В США применяется налог с продаж, величина которого меняется от штата к штату. В Калифорнии этот налог, как правило, составляет 8.75%. Сумма налога не указывается в продажной цене товара, а начисляется при оплате покупок. Покупатель выбрал в Wal Mart товары на сумму $39.53 без учёта налога с продаж. Какую сумму он заплатил в кассе?

Решение. Обозначим через x сумму налога и запишем условия задачи в виде процентной пропорции:

Это основная задача 1. По формуле (1.1) вычисляем сумму налога:

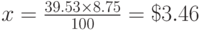
Следовательно, покупатель при оплате покупок заплатил сумму, равную

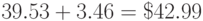
Обращаем ваше внимание на то, что знаки большинства валют указываются перед суммой. Знак рубля является исключением и ставится после суммы. Официальный знак рубля - буква Р с дополнительным элементом в виде горизонтальной черты, был утверждён 11 декабря 2013 г. Покажем как будут изображаться знаки популярных валют (доллар, евро, иена, английский фунт, рубль) в программе Excel при задании соответствующих финансовых форматов в ячейках:

Рис. 1.1. Знаки валют

Пример 2. В России в продажную цену товара включается налог на добавленную стоимость (НДС). Его величина для большинства товаров составляет 18%. Иногда он указывается отдельной строкой в кассовом чеке (это актуально для предпринимателей). При покупке товаров сумма НДС составила 48.66 руб. Какова стоимость товара без НДС?

Решение. Обозначим через x стоимость товара без НДС и запишем условие задачи в виде процентной пропорции:

Это основная задача 2. Находим значение x по формуле (1.2):

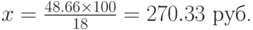
Пример 3. Покупатель приобрёл в магазине "Пятерочка" товары на сумму 110.90 руб. По дисконтной карте ему была предоставлена скидка, равная 7.50 руб. Чему равна величина скидки в процентах от суммы покупки?

Решение. Обозначим через x искомое число процентов и запишем условие задачи в виде процентной пропорции:

Это основная задача 3. Значение x находим по формуле (1.3):

Пример 4. Господин Н сначала владел 1000 акций компании К, что составляло 2.5% от общего числа акций этой компании. Чему стала равна его доля после покупки ещё 200 акций?

Решение. Обозначим через x число процентов, которое соответствует 1200 акций и запишем условие задачи в виде процентной пропорции:

Это основная задача 4. Значение x находим по формуле (1.4):

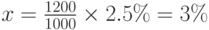
Не имеет никакого смысла складывать, вычитать или сравнивать количества процентов, относящиеся к разным базам. Например, если предприятие производит два продукта - A и B, причём продукт A приносит 20% прибыли, а продукт B 15% прибыли, то совершенно неверно заключить, что от производства этих двух продуктов предприятие получает 35% прибыли или что при производстве продукта A оно получит сумму денег на 5% большую, чем при производстве продукта B. Ответ зависит от пропорций выпуска продуктов. Подобные задачи мы рассмотрим ниже.

Пример 5. Господин Н, получив в наследство $65 000 купил на них две квартиры: однокомнатную за $25 000 и двухкомнатную за $40 000. Через год он продал эти квартиры, получив от продажи однокомнатной квартиры 40% прибыли, а от продажи двухкомнатной квартиры 30% прибыли. Сколько процентов прибыли господин Н получил от продажи двух квартир?

Решение. Вычислим сумму денег, полученную в качестве прибыли. По Формуле (1) суммы прибыли от продажи однокомнатной и двухкомнатной квартир равны, соответственно,

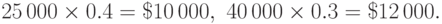
Всего господин Н получил прибыль, равную

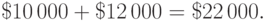
Требуется определить, сколько процентов составляет $22000 от $65 000. Обозначим искомое число процентов через x и найдем его значение по формуле (1.3):

Пример 6. Вычислим, на сколько процентов прибыль, полученная от продажи двухкомнатной квартиры господином Н из примера 5, больше, чем прибыль, полученная им от продажи однокомнатной квартиры.

Решение. В предыдущем примере мы уже нашли, что прибыль от продажи однокомнатной квартиры равна $10000, а от продажи двухкомнатной квартиры -$12000. Надо найти, на сколько процентов число $12 000 больше числа $10000. Базой (100%) в этом случае является число 10000. Вычислим, сколько процентов составляет число 12000 от числа 10000. Обозначим искомое число процентов через x и найдем его значение по формуле (1.3):

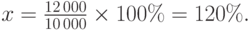
Следовательно, сумма прибыли, полученная от продажи двухкомнатной квартиры, на 20% больше, чем сумма прибыли, полученной от продажи однокомнатной квартиры.

В следующем примере рассматриваются так называемые безналоговые покупки. Приведём сначала краткую информацию об этом.

Безналоговые покупки в Европе. Когда вы делаете покупки в странах Европейского сообщества, то оплачиваете не только цену товара, но и налог на добавленную стоимость, который включается в продажную цену. Вы можете вернуть выплаченную сумму НДС, если получите при покупках чеки безналоговых покупок. Такие чеки выдаются во многих магазинах Европы. Безналоговые покупки в Европейском сообществе - это система возврата НДС для туристов, не являющихся гражданами Европейского сообщества. Сумма НДС возвращается при пересечении границы Европейского сообщества, если вы вывозите купленные товары с течение 90 дней со дня покупки и имеете на эти товары чеки безналоговых покупок. Когда вы покидаете Европейское сообщество, предъявите ваши покупки и чеки безналоговых покупок таможенным властям. Они поставят штамп на ваши чеки. После этого вы можете получить обратно выплаченную сумму НДС по чекам безналоговых покупок в специальных пунктах возврата налогов.

Пример 7. В Великобритании НДС для большинства товаров составляет 17.5%. НДС входит в продажную цену товара. Какой процент составляет налог на добавленную стоимость в продажной цене?

Решение. Цену товара без НДС примем за 100%. Тогда продажная цена товара составляет

Обозначим через x искомое число процентов и запишем условие задачи в виде процентной пропорции:

Это основная задача 3. Значение x находим по формуле(3):

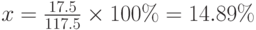
При процентных расчётах нередко допускаются ошибки, связанные с начислением сложного процента. Это понятие будет подробно рассматриваться в третьей и последующих лекциях. Здесь мы разберем только решение нескольких примеров, связанных с ним.

Пример 8. Некоторый товар подорожал в январе на 10% и в феврале ещё на 10%. На сколько процентов подорожал товар за два месяца?

Решение. Первоначальную цену товара примем за 100%. После первого повышения она стала равна

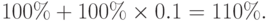
При втором повышении эта новая цена увеличится на 10%, то есть на 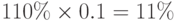от первоначальной цены. Таким образом, цена через два месяца составит

от первоначальной цены. Следовательно, цена товара за два месяца повысилась на 21%.

Замечание. Распространённая ошибка - просто сложить проценты:

Ошибка заключается в том, что при этом складывают проценты, начисленные на разные базы.

Пример 9. Цена товара уменьшилась в результате двух снижений цены на одно и то же число процентов с 800 руб. до 512 руб. На сколько процентов снижалась цена каждый раз?

Решение. Обозначим искомое число процентов через x. Первое снижение равно

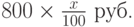
после чего цена стала равна

Эта новая цена снизилась при втором снижении на

и стала равна:

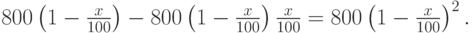
По условию задачи эта цена после второго снижения стала равна 512, то есть искомое число процентов x является корнем уравнения:

Так как снижение цены не может произойти более чем на 100%, то

поэтому последнее уравнение равносильно уравнению:

Замечание. Распространённая ошибка при решении последней задачи состоит в следующем. Вычисляют общее снижение цены за два раза:

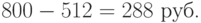
Далее находят, сколько процентов составляет число 288 от первоначальной цены 800 руб. по формуле(1.3):

Делят это число на 2 и получают 18%. Сущность ошибки и здесь состоит в том, что не учитывается, что проценты в первый и во второй раз должны начисляться на разные базы.