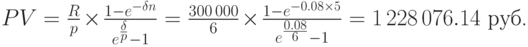Элементы финансовой математики
[+]
Лекция 7:

Приведенная ценность финансовой ренты
A
|
версия для печати
< Лекция 6 || Лекция 7: 123456789 || Лекция 8 >

7.3.3 Рента с непрерывным начислением процентов

Ещё раз отметим, что ренты с непрерывным начислением процентов широко применяются в Годовая рента

Применяя формулы из лекции 3 и 6, получаем:

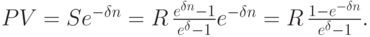
PV=Se^{-\delta n}=R\,\frac{e^{\delta n}-1}{e^{\delta}-1} e^{-\delta n}= R\,\frac{1-e^{-\delta n}}{e^{\delta}-1}.

Итак, приведённая ценность ренты равна:

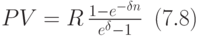
PV=R\,\frac{1-e^{-\delta n}}{e^{\delta}-1}\,\,\, (7.8)

p-срочная рента

Применяя формулы из лекций 3 и 6, получаем:

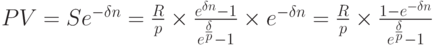
PV = Se^{-\delta n}=\frac{R}{p}\times\frac{e^{\delta n}-1}{e^{{\delta\over p}}-1}% \times e^{-\delta n}= \frac{R}{p}\times\frac{1-e^{-\delta n}}{e^{{\delta\over p}}-1}

Таким образом, приведённая ценность ренты равна:

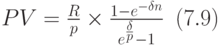
PV=\frac{R}{p}\times\frac{1-e^{-\delta n}}{e^{{\delta\over p}}-1}\,\,\, (7.9)

Рассмотрим примеры, при решении которых используются выведенные выше формулы.

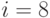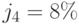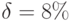Пример 63. Какую сумму необходимо положить в начальный момент в банк, чтобы иметь возможность в течение следующих 5 лет ежегодно снимать со счета 50 000 руб., исчерпав счет полностью к концу срока. Банк начисляет на вложенные в него деньги проценты по ставке: а) годовой i=8%, б) j_{4}=8\%, в) непрерывной \delta=8\%?

Решение. Во всех случаях требуется найти приведённую ценность годовой ренты. В случае а) проценты начисляются в конце года. Применяем формулу (7.6):

PV=Ra_{n;\,i}=50\,000\, a_{5;\,8\%}.

Вычисляем, что 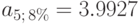a_{5;\,8\%}=3.9927 и подставляем в формулу:

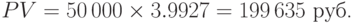
PV=50\,000\times 3.9927=199\,635\mbox{ руб.}

б) В этом случае проценты начисляются 4 раза в год. Применяем формулу (7.9) при n=5, m=4, j_{m}/m=8\%/4=2\%:

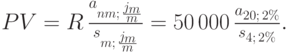
PV=R\,\frac{a_{nm;\,{j_{m}\over m}}}{s_{m;\,{j_{m}\over m}}}=% 50\,000\,\frac{a_{20;\,2\%}}{s_{4;\,2\%}}.

По формулам находим значения:

a_{20;\,2\%}=\frac{1-(1+0.02)^{-20}}{0.02}=16.3514 ,\\ s_{4;\,2\%}=\frac{(1+0.02)^{4}-1}{0.02}=4.1216.

Подставляем вычисленные значения и получаем ответ:

PV=50\,000\times\frac{16.3514}{4.1216}=198\,362.31\mbox{ руб.}

в) В этом случае применяем формулу (7.8) при 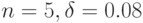n=5, \delta=0.08:

PV=R\,\frac{1-e^{-\delta n}}{e^{\delta}-1}=% 50\,000\,\frac{1-e^{-0.08\times 5}}{e^{0.08}-1}=197\,917.85\mbox{ руб.}

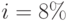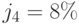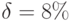Пример 64. Какую сумму необходимо положить в банк, чтобы в течение следующих 5 лет ежегодно получать 300 000 руб., полностью исчерпав счет к концу этого срока. Деньги будут сниматься каждые 2 месяца равными частями. Банк начисляет на находящиеся на счету деньги проценты по ставке: а) годовой i=8\%, б) годовой j_{4}=8\% , в) непрерывной годовой \delta=8\%.

Решение. о всех случаях требуется найти современную ценность p-срочной ренты при p=6.

а) В этом случае проценты начисляются только в конце года. Применяем формулу (7.5) при n=5, i=8%, p=6:

PV=Ra_{n;\,i}^{(p)}=300\,000\times a_{5;\,8\%}^{(6)}.

Вычисляем значение 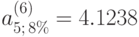a_{5;\,8\%}^{(6)} = 4.1238, подставляем его и получаем ответ:

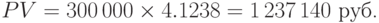
PV = 300\,000\times 4.1238=1\,237\,140\mbox{ руб.}

б) В этом случае проценты начисляются 4 раза в год. Применяем формулу (7.6) при n=5, m=4, j_{m}=8\%, p=6:

PV=\frac{R}{p}\times\frac{a_{mn;\,{j_{m}\over m}}}{s_{{m\over p};\,{j_{m}\over m}}}= \frac{300\,000}{6}\times\frac{a_{20;\,2\%}}{s_{{2\over 3};\,2\%}}.

По формулам вычисляем:

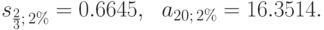
s_{{2\over 3};\,2\%}=0.6645,\ \ a_{20;\,2\%}=16.3514.

Находим современную ценность ренты:

PV=300\,000\times\frac{16.3514}{6\times 0.6645}=1\,230\,422.78\ \mbox{руб.}

в) В этом случае проценты начисляются непрерывно. Применяем формулу (7.9) при n=5, p=6, 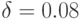\delta=0.08:

PV=\frac{R}{p}\times\frac{1-e^{-\delta n}}{e^{{\delta\over p}}-1}= \frac{300\,000}{6}\times\frac{1-e^{-0.08\times 5}}{e^{{0.08\over 6}}-1} = 1\,228\,076.14 \mbox{ руб.}
Дальше >>
< Лекция 6 || Лекция 7: 123456789 || Лекция 8 >

Вопросы и ответы

вопросов: 1
Иван каташинский
Иван каташинский
ответить