Простые проценты
2.1 Определение простых процентов
Если сумма P увеличивается на r%, то полученная в результате сумма S называется наращенной суммой и вычисляется по формуле:
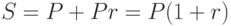
При этом величина P называется исходной суммой, а Pr - суммой начисленных процентов.
Пример 20. Сбербанк выплачивает по пенсионным вкладам 3.5% годовых (простые). Вычислим, какая сумма будет через год на счете пенсионера, положившего на счёт 1,200 руб. в начале года.
Решение. Через год на счету пенсионера будет сумма:

Если имеется несколько периодов времени, в каждый из которых исходная сумма P увеличивается на r%, то говорят, что на сумму P начисляются простые проценты. Наращенная сумма S, полученная в результате начисления n раз по r% на сумму P, выражается формулой:

Формула, выражающая наращенную сумму при начислении простых процентов, получена при условии, что число n периодов начисления процентов - целое. По определению мы введем такую же формулу для любого положительного (не обязательно целого) числа периодов, которое будем обозначать буквой t:
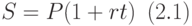
Необходимость начисления процентов за нецелое число периодов встречается в практике финансовых расчетов часто. Например, на депозит, пролежавший в банке 3 года и 3 месяца, банк должен начислить проценты за 3.25 периода.
Заметим, что при заключении финансовых контрактов обычно оговаривается наименьшая часть периода начисления процентов: например, каждый полный день (1/360 часть периода начисления, равного году). В этом случае t в формуле (2.1) принимает лишь значения соответственно k/360 или k/52 (k - целое). Например, если депозит пролежал в банке 2 года 16 дней, то

Для сравнения различных условий кредитования финансисты приводят ставку процента за произвольный период к годовой. Это правило в большинстве стран закреплено законом. Например, если банк даёт r% простых в год, то это соответствует квартальной ставке
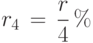 . Таким образом, при
. Таким образом, при 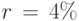 , имеем
, имеем 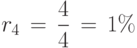 .
.
2.2 Разы и проценты
Когда в статистических отчётах, публицистике и в обыденной жизни сообщается об изменении какого-либо показателя, то это изменение в одних случаях указывается в процентах, а в других - в разах. И порой возникает путаница при переводе процентов в разы и разов в проценты.
Правило перевода предельно простое, если речь об увеличении (росте) некоторого показателя: при переводе процентов в разы надо, рассматривая процент как десятичную дробь, прибавить число 1; при переводе разов в проценты надо вычесть из разов 1 и результат перевести в проценты. Поясним на конкретных примерах, как получено и работает это правило.
Пример 21. На первой странице газеты "Ведомости" от 1 августа 2005 г. можно было увидеть заголовок: "Зарплата россиян за 1,5 года выросла в 1,5 раза". На сколько процентов увеличилась зарплата россиян за рассматриваемый период?
Решение. Обозначим через x среднюю зарплату в России в начале рассматриваемого периода (начало 2004 г.). Тогда из условия следует, что в конце рассматриваемого периода (середина 2005 г.) средняя зарплата составила 1.5x. Следовательно, зарплата увеличилась на
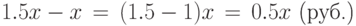
Мы так подробно расписали эти элементарные вычисления, чтобы было видно, что в круглой скобке из разов (1.5) вычитается 1. Переведем величину увеличения зарплаты в проценты от зарплаты в начале 2004 г.\ и получим, что зарплата увеличилась на 50%:

Рассмотрим теперь ситуацию, когда имеет место уменьшение некоторого показателя. Любое уменьшение можно считать ростом на отрицательное количество процентов. Для роста в таком понимании, если обозначить r. - величину роста, выраженную как десятичная дробь, то должно быть выполнено неравенство: 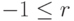 . Это неравенство означает, что процент уменьшения не может быть больше 100%, а процент увеличения может быть неограниченно большим. Такому обобщению понятия роста поставим в соответствие понятие коэффициент изменения. Коэффициент изменения - положительное число, на которое надо умножить начальное значение показателя, чтобы получить его конечное значение. При увеличении значения показателя коэффициент изменения будет больше 1, а при уменьшении - меньше 1. С учетом сказанного, можно сформулировать единое правило перевода процентов в коэффициент изменения: при переводе процентов в коэффициент изменения нужно, рассматривая процент как
десятичную дробь, прибавить 1.
. Это неравенство означает, что процент уменьшения не может быть больше 100%, а процент увеличения может быть неограниченно большим. Такому обобщению понятия роста поставим в соответствие понятие коэффициент изменения. Коэффициент изменения - положительное число, на которое надо умножить начальное значение показателя, чтобы получить его конечное значение. При увеличении значения показателя коэффициент изменения будет больше 1, а при уменьшении - меньше 1. С учетом сказанного, можно сформулировать единое правило перевода процентов в коэффициент изменения: при переводе процентов в коэффициент изменения нужно, рассматривая процент как
десятичную дробь, прибавить 1.
Приведём схематичное изображение этого правила:
Пример 22. Цена акции уменьшилась за год на 20%. Вычислим, чему равен коэффициент изменения цены акции.
Решение. Обозначим через x цену акции в начале года. По условию цена акции в конце года составила
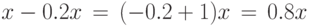
Следовательно, коэффициент изменения цены акции равен 0.8. Мы так подробно расписали эти элементарные вычисления, чтобы было видно, что в круглой скобке к процентам роста (-0.2) прибавляется 1.
Рассмотрим теперь ситуацию, когда имеет место уменьшение значения некоторого показателя x, которое выражается в разах. Предположим, что это значение уменьшилось в k раз. Это означает, что новое значение показателя равно x/k и составляет 1/k процентов от исходного значения. Соответственно, значение показателя изменилось на
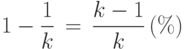
Таким образом, при уменьшении значения некоторого показателя правило перевода разов в проценты может быть сформулировано следующим образом: при переводе k разов в проценты нужно выразить в процентах дробь (k-1)/k.
Приведем теперь схематичное изображение общего правила перевода разов в проценты:
Пример 23. За 2 года цена некоторой модели цифрового фотоаппарата уменьшилась в 3 раза. Вычислим, на сколько процентов уменьшилась цена.
Решение. Используем приведенное выше правило перевода при k=3:
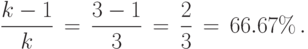
Следовательно, за 2 года цена фотоаппарата уменьшилась на 66.67%.


