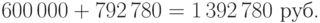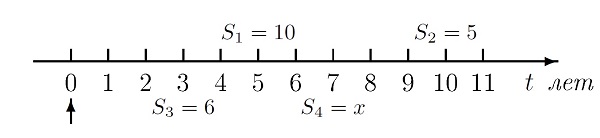Простые проценты
2.6 Учет векселей
Простые проценты применяются в финансовой операции, которая называется учетом векселей и заключается в следующем: банк покупает вексель на сумму S у его владельца до истечения срока оплаты векселя по цене P, меньшей, чем S. Цена S рассчитывается по формуле:
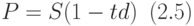
где t - число лет, остающееся с момента учета векселя до срока его оплаты, d% - учётная ставка, установленная банком.
Заметим, что процент наращения r и учётная ставка d характеризуют приращение денег в единицу времени в долях либо расходного платежа P, либо доходного платежа S:

Как следует из этих формул, величина ставки наращения r и учётной ставка d должна быть согласована с единицей измерения t. Например, если время измеряется в годах, то и соответствующая ставка будет годовая, а если время измеряется в месяцах, то - месячная.
Пример 28. Вексель выдан на 10 000 руб. с уплатой 15 октября. Владелец векселя учел его в банке 15 августа по учётной ставке 10%. Вычислим, какую сумму он получил. Вычислим также, какую сумму он получит, если срок уплаты по векселю 15 октября следующего года.
Решение. Число дней между 15 августа и 15 октября равно 60. Считая, что в году 360 дней (так принято при банковском учете), имеем  . По формуле (2.5) при S=10 000, d=0.1, t=1/6 получаем ответ на первый вопрос:
. По формуле (2.5) при S=10 000, d=0.1, t=1/6 получаем ответ на первый вопрос:
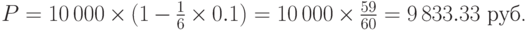
Число дней между 15 августа и 15 октября следующего года равно 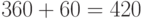 дней, т.е.,
дней, т.е.,

По формуле(2.5) при 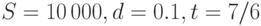 получаем ответ на второй вопрос:
получаем ответ на второй вопрос:

2.7 Простой дисконт
Простым дисконтом (по-английски - discount, по-итальянски - sconto) называется процентный доход, вычитаемый из ссуды в момент ее выдачи или взимаемый банком при учёте векселя. Термином дисконт называют порой также сам учёт векселей.
Если процентная ставка простого дисконта - r%, величина ссуды - S (эта сумма должна быть возвращена), P - величина ссуды, полученная в момент её выдачи, t лет - срок, на который выдаётся ссуда, то простой дисконт равен Srt и P=S-Srt . Следовательно, имеем формулу:

Пример 29. Финансовая компания даёт ссуду 500 000 руб. на 3 года под простой дисконт, равный 5% в год. Определим, какую сумму получит клиент в момент получения ссуды.
Решение. Находим P по формуле (2.6) при 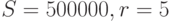 :
:
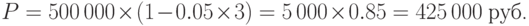
2.8 Приведение ценности денег к одному моменту времени
В теории и на практике нам постоянно приходится решать вопрос о том, как соотносятся между собой суммы денег, полученные в различные моменты времени. Финансовая теория в этом вопросе придерживается принципа невозможности межвременного арбитража: ценность суммы денег S в фиксированный момент в будущем эквивалентна такой сумме денег P в текущий момент времени, которая будучи подходящим образом использована на финансовом рынке, принесет нам ровно сумму S на рассматриваемый будущий момент времени. Вопрос о том, что следует понимать под подходящим использованием, является одной из серьезных задач теории корпоративных финансов. Достаточно отметить, что здесь необходимо учитывать такой фактор финансового рынка как риск - различное использование денег связано и с принятием инвестором различного риска. В простейшей постановке, принятой в этой книге, предполагается, что операции носят безрисковый характер.
Если в качестве подходящего использования денег мы рассматриваем возможность инвестировать их (положить в банк, купить облигации и т.п.) под простой годовой процент r%, то сумма денег S через t лет, согласно формуле (2.2), будет равна P(1+rt). Поэтому приведенная (или современная) ценность P суммы S, которая будет получена через t лет, вычисляется по формуле (2.2):
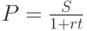
Вычисление приведенной ценности суммы денег называется дисконтированием этой суммы.
Термин "приведенная" ценность не носит абсолютного характера - в качестве момента приведения (или точки отсчёта) в расчётах может быть взят любой момент времени. Обычно понятие приведённой ценности применяется к потоку платежей (во времени). Рассмотрим простейшие примеры приведения с использованием простых процентов.
Два контракта называют эквивалентными, если приведенные ценности потоков платежей по этим контрактам равны. Рассмотрим пример.
Пример 30. Фирма обязалась заплатить за полученное от города производственное помещение 1 000 000 руб. через 5 лет и еще 500 000 руб. через 10 лет от настоящего момента. Фирма желает рассчитаться быстрее: уплатить 600 000 руб. через 3 года, а остальной долг выплатить через 7 лет (от настоящего момента). Вычислим, какая сумма должна быть выплачена через 7 лет, если на деньги начисляются 8% простых в год.
Решение. Изобразим суммы (в 100 тыс. руб.) первого контракта над осью времени, а второго - под осью. Стрелкой внизу указан момент времени, который выбран за точку отсчёта.
Дисконтируя все суммы на момент 0, находим приведенные к моменту~0 ценности этих сумм:
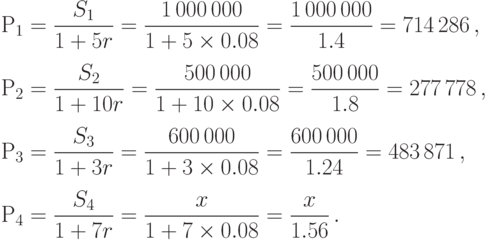
Контракты эквивалентны, если выполнено равенство  . Из этого равенства получаем уравнение:
. Из этого равенства получаем уравнение:

решив которое, находим значение x:
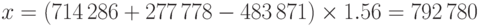
Следовательно, сократив сроки платежей, фирма уменьшила суммарные выплаты с 1 500 000 руб. до