Поиск на графе

Поиск в ширину

Предположим, что нам нужно найти кратчайший путь между двумя конкретными вершинами графа — такой путь, соединяющий эти вершины, что никакой другой путь между этими вершинами не содержит меньшее число ребер. Классический метод решения этой задачи, получивший название поиска в ширину (BFS — breadth-first search), также лежит в основе многочисленных алгоритмов обработки графов; ему и посвящен данный раздел. Поиск в глубину мало пригоден для решения этой задачи, поскольку порядок прохождения им графа никак не связан с поиском кратчайших путей. А вот поиск в ширину очень удобен для этого. Поиск кратчайшего пути от вершины v к вершине w мы начнем с того, что попытаемся найти вершину w среди всех вершин, в которые можно перейти по одному ребру из вершины v, затем проверим все вершины, в которые можно перейти по двум ребрам и т.д.

Когда во время просмотра графа мы попадаем в вершину, из которой исходят более одного ребра, мы выбираем одно из них и запоминаем остальные для последующего просмотра. В поиске в глубину для этой цели применяется стек магазинного типа (которым управляет система при вызовах рекурсивной функции поиска). Применение правила LIFO (Last In First Out — последним пришел, первым вышел), которое характеризует работу стека магазинного типа, соответствует исследованию соседних коридоров в лабиринте: из всех еще не исследованных коридоров выбирается последний обнаруженный. В поиске в ширину необходимо исследовать вершины в порядке их удаления от исходной точки. В случае реального лабиринта для такого исследования может потребоваться целая бригада; однако в компьютерной программе эта цель достигается намного проще: вместо стека используется очередь FIFO (First In First Out — первым пришел, первым вышел).

Программа 18.8 представляет собой реализацию поиска в ширину. В ней используется очередь всех ребер, которые соединяют посещенные вершины с еще не посещенными. Вначале в очередь помещается фиктивная петля с исходной вершиной, а затем до исчерпания очереди выполняются следующие действия:

• Выбираем ребра из очереди до тех пор, пока не найдем такое ребро, которое указывает на непосещенную вершину.
• Посещаем эту вершину; заносим в очередь все ребра, исходящие из этой вершины в еще не посещенные вершины.

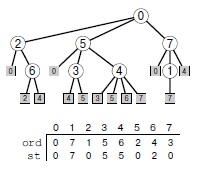
На рис. 18.21 показано выполнение поиска в ширину на конкретном примере.

Рис. 18.21. Поиск в ширину

Здесь показаны шаги поиска в ширину на примере графа. Мы начинаем его со всех ребер, смежных с находящейся в очереди исходной вершиной (вверху слева). Потом мы переносим ребро 0-2 из очереди в дерево и обрабатываем инцидентные ему ребра 2-0 и 2-6 (вторая диаграмма сверху слева). Мы не помещаем ребро 2-0 в очередь, поскольку вершина 0 уже содержится в дереве.

Затем мы переносим из очереди в дерево ребро 0-5; одно из ребер, инцидентных вершине 5, также не приводит в новую вершину, однако мы добавляем в очередь ребра 5-3 и 5-4 (третья диаграмма сверху слева). После этого мы добавляем в дерево ребро 0-7 и заносим в очередь ребро 7-1 (внизу слева).

Ребро 7-4 не выделено серым цветом: его можно не заносить в очередь, т.к. другое ребро уже привело нас в вершину 4, и она уже помещена в очередь. Для завершения поиска мы удаляем оставшиеся ребра из очереди, полностью игнорируя при этом серые ребра, когда они подходят к началу очереди (справа). Ребра заносятся в очередь и выбираются из нее в порядке их удаленности от вершины 0.

Программа 18.8. Поиск в ширину

Данный класс поиска на графе при посещении вершины просматривает все инцидентные ей ребра и помещает ребра, ведущие в непосещенные вершины, в очередь вершин, ожидающих посещения. Маркировка вершин в порядке их посещения хранится в векторе ord. Функция search, вызываемая конструктором, строит явное представление дерева BFS родительскими ссылками (ребра, которые впервые приводят нас в каждый узел) в другом векторе st, который затем можно использовать для решения базовой задачи поиска кратчайшего пути (см. текст).

  #include "QUEUE.cc"
  template <class Graph>
  class BFS : public SEARCH<Graph>
    { vector<int> st;
      void searchC(Edge e)
        { QUEUE<Edge> Q;
          Q.put(e);
          while (!Q.empty())
            if (ord[(e = Q.get()).w] == -1)
              { int v = e.v, w = e.w;
                ord[w] = cnt++; st[w] = v;
                typename Graph::adjIterator A(G, w);
                for (int t = A.beg(); !A.end(); t = A.nxt())
                  if (ord[t] == -1) Q.put(Edge(w, t));
              }
        }
    public:
      BFS(Graph &G) : SEARCH<Graph>(G), st(G.V(), -1)
        { search(); } 
      int ST(int v) const { return st[v]; }
   };
      

Как было показано в разделе 18.4, поиск в глубину подобен исследованию лабиринта одним человеком. Поиск в ширину можно сравнить с исследованием группой людей, которые расходятся веером по всем направлениям. Методы DFS и BFS отличаются друг от друга во многих отношениях, но между этими двумя методами существует глубинная связь — о ней было сказано в кратком анализе методов в "Рекурсия и деревья" . В разделе 18.8 мы рассмотрим обобщенный метод поиска на графе, который можно настроить так, чтобы он включал в себя и оба эти алгоритма, и множество других. Каждый алгоритм обладает особыми динамическими характеристиками, которые мы используем для решения соответствующих задач обработки графов. В случае поиска в ширину нас наиболее интересует расстояние каждой вершины от исходной вершины (длина соединяющего их кратчайшего пути).

В случае поиска в глубину мы выявляли динамические характеристики этого алгоритма с помощью леса поиска DFS, который описывает структуру рекурсивных вызовов алгоритма. Основное свойство этого леса состоит в том, что он представляет пути из каждой вершины в точку, откуда начался поиск содержащего ее связного компонента. Как видно из реализации и рис.18.22, такое остовное дерево помогает также понять суть поиска в ширину. Как и в случае DFS, мы имеем лес, описывающий динамику поиска: деревья соответствуют связным компонентам, узлы — вершинам графа, а ребра дерева — ребрам графа. Поиск в ширину соответствует обходу каждого дерева этого леса по уровням. Как и в случае DFS, для явного представления леса родительскими ссылками используется вектор, индексированный именами вершин. Этот лес содержит важную информацию о структуре графа:

Как показано на рис. 18.21 и сказано в "Рекурсия и деревья" , нет необходимости помещать в очередь ребро с такой же конечной вершиной, что и у хотя бы одного ребра, которое уже находится в очереди, поскольку правило FIFO гарантирует обработку ребра, которое уже находится в очереди (и посещение соответствующей вершины), раньше, чем алгоритм доберется до нового ребра. Один из способов реализации этого правила заключается в использовании реализации АТД очереди, в которой одинаковые элементы запрещены принципом игнорирования новых элементов (см. "Абстрактные типы данных" ). Другой способ — применение для этой цели глобального вектора пометки вершин: вместо пометки вершины в момент ее извлечения из очереди как посещенной, это делается при занесении ее в очередь. Проверка, помечена ли вершина (изменилось ли значение соответствующего элемента с начального сигнального значения), как раз и запрещает включение в очередь других ребер, которые указывают на эту вершину. Это изменение, показанное в программе 18.9, позволяет получить реализацию поиска в ширину, в очереди которой не бывает более V ребер (в каждую вершину ведет не более одного ребра).

Рис. 18.22. Дерево BFS

Это дерево представляет собой компактное описание динамических характеристик поиска в глубину, аналогично дереву, которое показано на рис. 18.9. Обход дерева по уровням показывает, как выполняется поиск: сначала мы посещаем вершину 0, потом вершины 2, 5 и 7, затем, находясь в 2, мы выясняем, что в вершине 0 мы уже были, и направляемся в 6 и т.д. У каждого узла дерева имеются дочерние узлы, которые представляют узлы, смежные с этим узлом, в том порядке, в каком они рассматриваются алгоритмом BFS. Как и на рис. 18.9, ссылки дерева BFS соответствуют ребрам графа: если заменить ребра, ведущие во внешние узлы, на линии, ведущие в заданный узел, то мы получим чертеж графа. Ссылки, ведущие во внешние узлы, представляют собой ребра, которые не были помещены в очередь, потому что они ведут в помеченные узлы: это либо родительские ссылки, либо перекрестные ссылки, которые указывают на узел, находящийся на том же уровне или на уровне, более близком к корню дерева.

Вектор st являетсяпредставлени-ем дерева родительскими ссылками, которое можно использовать для поиска кратчайшего пути из любого узла в корень. Например, 3-5-0 — путь в графе из 3 в 0, поскольку st[3] равно 5, а st[5] равно 0. Более короткого пути из 3 в 0 не существует.

Программа 18.9. Усовершенствованный BFS

Чтобы очередь, используемая при выполнении BFS, содержала не более V элементов, мы помечаем вершины в момент занесения их в очередь.

  void searchC(Edge e)
    { QUEUE<Edge> Q;
      Q.put(e); ord[e.w] = cnt++;
      while (!Q.empty())
        { e = Q.get(); st[e.w] = e.v;
          typename Graph::adjIterator A(G, e.w);
          for (int t = A.beg(); !A.end(); t = A.nxt())
            if (ord[t] == -1)
              { Q.put(Edge(e.w, t)); ord[t] = cnt++; }
        }
     }
      

Поиск в ширину позволяет решить задачи нахождения остовного дерева, связных компонентов, поиска вершин и ряд других базовых задач связности, которые были описаны в разделе 18.4, поскольку рассмотренные решения зависят только от способности алгоритма поиска просмотреть все узлы и все ребра, связанные с исходной точкой. Как мы увидим, алгоритмы BFS и DFS лежат в основе многочисленных алгоритмов, обладающих этим свойством. Как было сказано в начале данного раздела, алгоритм BFS интересует нас в основном потому, что он является естественным алгоритмом поиска на графе, когда требуется найти кратчайший путь между двумя заданными вершинами. Теперь мы рассмотрим конкретное решение этой задачи и его расширение для решения двух других сходных задач.

Кратчайший путь. Нужно найти кратчайший путь на графе из v в w. Эту задачу можно выполнить, запустив процесс поиска в ширину, который создает в векторе st представление родительскими ссылками дерева поиска из v и останавливается по достижении вершины w. Путь вверх по дереву из w в v и является кратчайшим. Например, после построения экземпляра bfs класса BFS<Graph> клиент может использовать следующий код для вывода пути из w в v:

  for (t = w; t != w; t = bfs.ST(t)) cout << t << "-";
  cout << v << endl;
      

Чтобы получить путь из v в w, нужно заменить в этом коде операции cout операциями занесения в стек и добавить цикл, который выводит индексы этих вершин после выталкивания их из стека. Либо можно запустить поиск из w и остановить его по достижении v.

Кратчайшие пути из одного источника. Нужно найти кратчайшие пути, соединяющие заданную вершину v со всеми другими вершинами графа. Эту задачу позволяет решить полное дерево BFS с корнем в вершине v: путь из каждой вершины в корень является кратчайшим путем в корень. Поэтому для решения этой задачи необходимо выполнить поиск в ширину из вершины v до полного завершения. Полученный при этом вектор st является представлением дерева BFS родительскими ссылками, а код из предыдущего абзаца позволяет получить кратчайший путь в любую другую вершину w.

Кратчайшие пути для всех пар вершин. Нужно найти кратчайшие пути, соединяющие каждую пару вершин графа. Эту задачу можно выполнить с помощью класса BFS, который решает задачу с одним источником для каждой вершины графа и использует функции-члены, которые могут эффективно обрабатывать большое количество запросов на определение кратчайших путей, сохраняя длины путей и представления деревьев родительскими ссылками для каждой вершины (см. рис. 18.23). Такая предварительная обработка требует времени, пропорционального VE, и объема памяти, пропорционального V², что делает невозможной обработку больших разреженных графов. Однако она позволяет строить АТД с оптимальной производительностью: после затраты времени на предварительную обработку (и памяти для сохранения результатов этой обработки) можно вычислять длины кратчайших путей за постоянное время, а сами пути — за время, пропорциональное их длине (см. упражнение 18.55).

Такие решения на основе BFS вполне эффективны, однако здесь мы не будем рассматривать конкретные реализации, поскольку они представляют собой специальные случаи алгоритмов, которые будут подробно рассмотрены в "Кратчайшие пути" . Термин кратчайший путь в отношении графов обычно используется для описания соответствующих задач в орграфах и сетях. Этой теме посвящена "Кратчайшие пути" . Приведенные там решения являются строгими обобщениями описанных здесь решений на базе BFS.

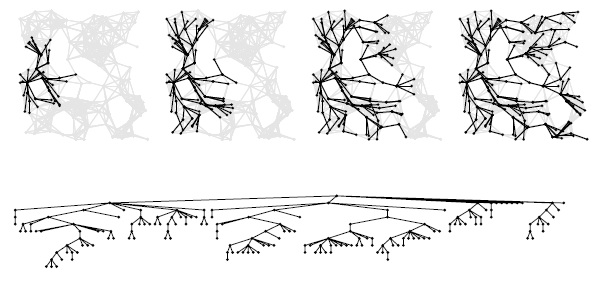
Базовые характеристики динамики поиска существенно отличаются от аналогичных характеристик поиска в глубину — см. пример для большого графа на рис. 18.24 и сравните его с рис. 18.13. Дерево имеет небольшую глубину, зато большую ширину. Оно демонстрирует множество отличий поиска в ширину на графе от поиска в глубину. Например:

• Существует относительно короткий путь, соединяющий каждую пару вершин графа.
• Во время поиска большая часть вершин смежна с многими непосещенными вершинами.

Опять-таки, этот пример типичен для поведения, которое мы ожидаем от поиска в ширину, однако следует тщательно проверять подобные факты для интересующих нас моделей графов и графов, с которыми приходится сталкиваться на практике.

Рис. 18.23. Пример определения кратчайших путей для всех пар вершин

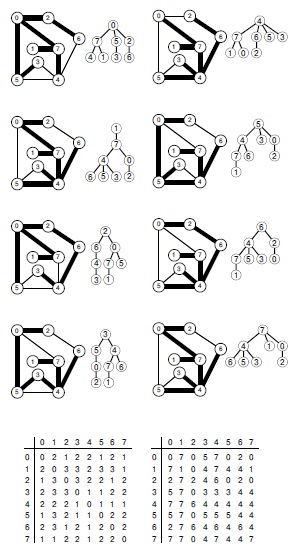
Эти диаграммы описывают результат выполнения поиска в ширину из каждой вершины, т.е. вычисления кратчайших путей, соединяющих все пары вершин. Каждый поиск приводит к построению дерева BFS, которое определяет кратчайшие пути, соединяющие все вершины графа с вершиной в корне дерева. Результаты всех поисков сводятся в две матрицы, показанные в нижней части рисунка.

В левой матрице элемент на пересечении строки v и столбца w содержит длину кратчайшего пути из v в w (глубину v в дереве w). Каждая строка правой матрицы содержит массив st для соответствующего поиска. Например, кратчайший путь из 3 в 2 состоит из трех ребер, как показывает элемент левой матрицы, расположенный на пересечении строки 3 и столбца 2. Третье сверху слева дерево BFS говорит, что это путь 3-4-6-2 — данная информация закодирована в строке 2 правой матрицы. При наличии нескольких кратчайших путей матрица не обязательно должна быть симметричной, поскольку найденные пути зависят от порядка выполнения поиска в ширину. Например, дерево BFS, показанное внизу слева, и строка 3 правой матрицы говорят, что кратчайшим путем из 2 в 3 является 2-0-5-3.

Рис. 18.24. Поиск в ширину

Данный рисунок показывает, что поиск в ширину выполняется в случайном евклидовом графе с близкими связями (слева) в том же стиле, что и на рис. 18.13. Как видно из этого примера, дерево BFS для таких графов (а также для многих других видов графов, которые часто встречаются на практике) обычно имеет малую глубину и большую ширину. То есть вершины обычно соединены между собой довольно короткими путями. Различие между формами деревьев DFS и BFS свидетельствуют о существенном различии динамических характеристик этих алгоритмов.

Поиск в глубину прокладывает свой путь в графе, запоминая в стеке точки ответвления других путей; поиск в ширину проходит по графу, используя очередь для запоминания границ, которых он достиг. Поиск в глубину исследует граф, выискивая вершины, далекие от исходной точки и переходя к рассмотрению более близких вершин только после выхода из тупиков. Поиск в ширину полностью покрывает область вокруг исходной точки и удаляется от нее только после просмотра ближайших окрестностей. Порядок посещения вершин зависит от структуры и представления графа, однако эти глобальные свойства деревьев поиска больше зависят от алгоритмов, чем от самих графов или их представлений.

Главное для понимания алгоритмов обработки графов — уяснить не только то, что существуют различные стратегии поиска как эффективное средство изучения различных свойств графов, но и то, что многие из них можно реализовать стандартным путем. Например, поиск в глубину, показанный на рис. 18.13, обнаруживает, что в графе имеется длинный путь, а поиск в ширину, изображенный на рис. 18.24, говорит о том, что в графе присутствуют многочисленные короткие пути. Но, несмотря на упомянутые различия в динамике, алгоритмы DFS и BFS имеют много общего. Они существенно различаются лишь структурой данных, которая используется для хранения еще не исследованных ребер (и случайной возможностью использовать рекурсивную реализацию DFS с системной поддержкой неявного стека). Теперь мы обратимся к обобщенным алгоритмам поиска на графах, которые охватывают как DFS и BFS, так и множество других полезных стратегий, и могут служить основой для решения разнообразных классических задач обработки графов.

Упражнения

18.50. Начертите лес BFS, построенный стандартным BFS по спискам смежности для графа

3-71-47-80-55-23-82-90-64-92-66-4.

18.51. Начертите лес BFS, построенный стандартным BFS по матрице смежности для графа

3-71-47-80-55-23-82-90-64-92-66-4.

18.52. Измените программы 18.8 и 19.9, чтобы использовать в них контейнер queue из библиотеки STL вместо АТД из "Абстрактные типы данных" .

18.53. Приведите реализацию BFS (на основе программы 18.9), которая использует очереди вершин (см. программу 5.22). Включите в нее проверку, не допускающую занесения в очередь одинаковых вершин.

18.54. Приведите матрицы всех кратчайших путей (в стиле рис. 18.23) для графа 3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4,

представленного матрицей смежности.

18.55. Разработайте класс поиска кратчайших путей, который после предварительной обработки отвечает на запросы о кратчайших путях. А именно, определите двухмерную матрицу как приватный член данных и напишите конструктор, который присваивает значения всем ее элементам, как показано на рис. 18.23. Затем напишите две функции запросов: функцию length(v, w), которая возвращает длину кратчайшего пути между вершинами v и w, и функцию path(v, w), которая возвращает вершину, смежную с v на кратчайшем пути между v и w.

18.56. Что можно узнать из дерева BFS о расстоянии между вершинами v от w, когда ни одна из них не является корнем этого дерева?

18.57. Разработайте класс, объектам которого известна длина пути, достаточного для соединения любой пары вершин конкретного графа. (Эта величина называется диаметром графа). Примечание: Необходимо сформулировать соглашение, какое значение возвращать, если граф окажется несвязным.

18.58. Приведите простой и оптимальный рекурсивный алгоритм вычисления диаметра дерева (см. упражнение 18.57).

18.59. Добавьте в класс BFS из программы 18.9 функции-члены (и соответствующие приватные члены данных), возвращающие высоту дерева BFS и процент ребер, которые необходимо обработать, чтобы добраться до каждой вершины.

18.60. Эмпирически определите средние значения величин, описанных в упражнении 18.59, для графов различных размеров и построенных на основе различных моделей (упражнения 17.64—17.76).