|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Поиск на графе
Разделимость и двусвязность
Для демонстрации широких возможностей DFS как основы алгоритмов обработки графов мы обратимся к задачам, связанным с обобщенным понятием связности в графах. Мы займемся изучением вопросов такого рода: пусть заданы две вершины, существуют ли два различных пути, связывающих эти вершины?
В некоторых ситуациях, когда важно, чтобы граф был связным, может оказаться существенным тот факт, что он остается связным, если убрать из него какую-либо вершину или ребро. То есть иногда нужно иметь более одного пути между каждой парой вершин графа с тем, чтобы застраховаться от возможных отказов. Например, из Нью-Йорка можно долететь в Сан-Франциско, даже если аэропорт в Чикаго завален снегом, т.к. имеется рейс через Денвер. Или возможна ситуация во время военных действий, когда желательно проложить такую железнодорожную сеть, что противнику для нарушения железнодорожного сообщения понадобится разрушить по меньшей мере две станции. Аналогично, было бы хорошо проложить соединения в интегральной схеме или в сети связи таким образом, что при обрыве какого-либо провода или отказе соединения остальная часть схемы продолжала работать.
Все эти примеры демонстрируют две принципиально различные концепции: в случае интегральной схемы и сети связи мы заинтересованы в сохранении связности при удалении ребра; в случае авиа- и железнодорожных сообщений нужно сохранить связность при удалении вершины. Мы начнем с подробного анализа первого случая.
Определение 18.1. Мостом (bridge) в графе называется ребро, после удаления которого связный граф распадается на два не связанных между собой подграфа. Граф, у которого нет мостов, называется реберно-связным (edge-connected).
Когда мы говорим об удалении ребра, мы имеем в виду удаление этого ребра из множества ребер, которое определяет граф, даже если после такого удаления одна или обе вершины этого ребра станут изолированными. Реберносвязный граф остается связным при удалении из него любого одного ребра. В некоторых контекстах естественнее говорить о разделении графа, а не о возможности графа оставаться связным. Поэтому мы будем свободно пользоваться альтернативной терминологией, которая делает акцент на таких моментах: граф, который не является реберно-связным, назовем реберно-разделимым (edge-separable), а мосты назовем ребрами разделения (separation edge).
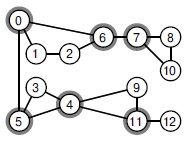
Этот граф не является реберно-связным. Ребра 0-5, 6-7 и 11-12 (заштрихованы) представляют собой ребра разделения (мосты). Граф содержит четыре реберно-связных компонента: один включает вершины 0, 1, 2 и 6; другой — вершины 3, 4, 9 и 11; третий — вершины 7, 8 и 10; последний состоит из единственной вершины 12.
Если в реберно-разделимом графе удалить все мосты, он распадется на реберно-связные компоненты (edge-connected components) или компоненты, связанные мостами (bridge-connected components) — максимальные подграфы, не содержащие мостов. На рис. 18.16 показан небольшой пример, иллюстрирующий эти понятия.
На первый взгляд выявление мостов в графе является нетривиальной задачей обработки графов, но на самом деле для ее решения достаточно алгоритма DFS и применения уже рассмотренных основных свойств деревьев DFS. В частности, обратные ребра не могут быть мостами, ведь мы знаем, что пары узлов, которые они соединяют, соединены также и путем в дереве DFS. Более того, в рекурсивную функцию несложно добавить условие для проверки, являются ли ребра дерева мостами. Основная идея четко сформулирована ниже и проиллюстрирована на рис. 18.17.
Лемма 18.5. В любом дереве DFS древесное ребро v-w является мостом тогда и только тогда, когда не существуют обратные ребра, соединяющие одного из потомков w с предком w.
Доказательство. Если такое ребро существует, то v-w не может быть мостом. С другой стороны, если v-w не есть мост, то в графе должен быть другой путь из w в v, отличный от w-v. Каждый такой путь должен содержать одно из таких ребер. 
Эта лемма эквивалентна утверждению, что единственная ссылка поддерева с корнем в w, указывающая на узел, который не входит в это поддерево — это родительская ссылка из w назад в v. Это условие соблюдается тогда и только тогда, когда каждый путь, соединяющий любой узел в поддереве узла w, с любым узлом, не принадлежащим этому поддереву, содержит ребро v-w. Другими словами, удаление ребра v-w отделяет подграф, соответствующий поддереву узла w, от остальной части графа.
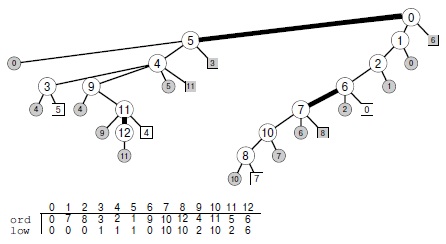
Программа 18.7 показывает, как можно изменить поиск в глубину, чтобы он мог выявлять мосты в графах с помощью программы 18.5. Для каждой вершины v рекурсивная функция вычисляет минимальный прямой номер, до которого можно дойти через последовательность из нуля или более ребер дерева с последующим единственным обратным ребром из любого узла поддерева с корнем в вершине v. Если вычисленный номер равен прямому номеру вершины v, то не существует ребра, связывающего потомка вершины v с ее предком — то есть найден мост.
Здесь приведено дерево DFS для графа с рис. 18.16. Узлы 5, 7 и 12 обладают тем свойством, что никакое обратное ребро не соединяет потомка с предком, и этим свойством не обладают никакие другие узлы. Поэтому удаление ребра между одним из этих узлов и его родительским узлом отделит поддерево с корнем в этом узле от остальной части графа. То есть ребра 0-5, 11-12 и 6-7 являются мостами. Массив low, индексированный именами вершин, используется для отслеживания минимального прямого номера (значение ord), на который указывает любое обратное ребро в поддереве, корнем которого является эта вершина. Например, low[9] содержит значение 2, т.к. одно из обратных ребер в поддереве с корнем в 9 указывает на 4 (вершина с прямым номером 2), и никакое другое обратное ребро не указывает на более высокую вершину в этом дереве. Для узлов 5, 7 и 12 значение low равно значению ord.
Программа 18.7. Реберная связность
Этот класс DFS подсчитывает количество мостов в графе. Клиент может использовать объект EC для определения количества реберно-связных компонентов. Добавление функции-члена, проверяющей, содержатся ли какие-либо две вершины в одном и том же реберно-связном компоненте, предлагается как самостоятельное упражнение (см. упражнение 18.36). Вектор low содержит минимальные прямые номера, которые могут быть достигнуты из каждой вершины через некоторую последовательность древесных ребер, за которой следует одно обратное ребро.
template <class Graph>
class EC : public SEARCH<Graph>
{ int bcnt;
vector <int> low;
void searchC(Edge e)
{ int w = e.w;
ord[w] = cnt+ + ; low[w] = ord[w];
typename Graph::adjIterator A(G, w);
for (int t = A.beg(); !A.end(); t = A.nxt())
if (ord[t] == -1)
{ searchC(Edge(w, t));
if (low[w] > low[t]) low[w] = low[t];
if (low[t] == ord[t])
bcnt++; // w-t является мостом
}
else if (t != e.v)
if (low[w] > ord[t]) low[w] = ord[t];
}
public:
EC(const Graph &G) : SEARCH<Graph>(G),
bcnt(0), low(G.V(), -1)
{ search(); }
int count() const { return bcnt+1; }
};
Вычисления для каждой вершины достаточно просты: мы просматриваем список смежности, отслеживая минимальные номера, которых можно достичь, проходя по каждому ребру. Для древесных ребер вычисления выполняются рекурсивно; для обратных ребер используется прямой номер смежной вершины. Если вызов рекурсивной функции для ребра w-t не находит путь к узлу с меньшим прямым номером, чем прямой номер узла t, то ребро w-t является мостом.
Лемма 18.6. Мосты графа можно найти за линейное время
Доказательство. Программа 18.7 представляет собой разновидность поиска в глубину с несколькими дополнительными проверками, которые выполняются за постоянное время. Поэтому из лемм 18.3 и 18.4 непосредственно следует, что поиск мостов в графе выполняется за время, пропорциональное V2 для представления матрицей смежности и V + E для представления списками смежности. 
В программе 18.7 для исследования свойств графа используется поиск в глубину. Разумеется, представление графа влияет на порядок поиска, но оно никак не влияет на результаты, т.к. мосты — характеристика графа, а не способа его представления или поиска на нем. Как всегда, любое дерево DFS — это просто еще одно представление графа, поэтому все такие деревья обладают одними и теми же свойствами связности. Корректность алгоритма зависит от этого фундаментального факта. Например, на рис. 18.18 показан другой поиск на том же графе; он начинается с другой вершины, но, естественно, обнаруживает те же самые мосты. Несмотря на лемму 18.6, при исследовании различных деревьев DFS одного и того же графа стоимость поиска может зависеть не только от свойств графа, но и от свойств дерева DFS. Например, объем памяти, необходимой для стека, который обеспечивает поддержку рекурсивных вызовов, больше для примера на рис. 18.18, чем для примера на рис. 18.17 рис. 18.17.
На этой диаграмме показано дерево DFS для графа с рис. 18.16, которое отлично от дерева, изображенного на рис. 18.17 — там поиск начинается с другого узла. Узлы и ребра просматриваются в совершенно другом порядке, но мосты находятся (естественно) одни и те же. В этом дереве вершины 0, 7 и 11 — это вершины, для которых значение low равно значению ord, поэтому ребра, соединяющие каждую из этих вершин с их родителями (соответственно, 12-11, 5-0 и 6-7) являются мостами.
Как и в случае обычной связности в программе 18.4, можно воспользоваться программой 18.7 для построения класса, который сможет проверить, является ли заданный граф реберно-связным, либо подсчитать количество реберно-связных компонентов. При желании, как и для программы 18.4, можно предоставить клиентам возможность создавать (за линейное время) объекты, способные за постоянное время отвечать на запросы, находятся ли две заданные вершины в одном и том же реберно-связном компоненте (см. упражнение 18.36).
Мы завершим этот раздел рассмотрением других обобщений понятия связности, включая задачу определения конкретных вершин, критичных для сохранения связности графа. Таким образом мы соберем в одном месте базовый материал, необходимый для изучения более сложных алгоритмов, которые будут рассматриваться в "Потоки в сетях" . Если вы впервые сталкиваетесь с задачами связности графов, вы можете просто перейти к разделу 18.7 и вернуться сюда перед чтением "Потоки в сетях" .
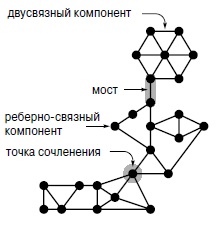
Этот граф состоит из двух реберно-связных компонентов и одного моста. К тому же реберно-связный компонент, расположенный над мостом, является двусвязным, а компонент ниже моста состоит из двух двусвязных компонентов, соединенных точкой сочленения.
Когда речь идет об удалении вершины, то при этом подразумевается и удаление всех инцидентных ей ребер. Как показано на рис. 18.19, при удалении любой из вершин моста нарушается связность графа (если, конечно, этот мост не был единственным ребром, инцидентным одной или обеим вершинам), но это свойство присуще и другим вершинам, не связанным с мостами.
Определение 18.2. Точка сочленения (articulation point) графа — это вершина, при удалении которой связный граф распадается по меньшей мере на два непересекаю-щихся подграфа.
Точки сочленения графа мы будем также называть вершинами разделения (separation vertex) или разрезающими вершинами (cut vertex). Граф, в котором нет вершин разделения, можно было бы назвать " вершинно-связным " , но мы воспользуемся другой, хотя в конечном счете и эквивалентной, терминологией.
Определение 18.3. Граф называется двусвязным (biconnected), если каждая пара его вершин соединена двумя непересекающимися путями.
Требование непересекающихся (disjoint) путей отличает двусвязность от реберной связности. Другое определение реберной связности — когда каждая пара вершин связана двумя путями без общих ребер, хотя эти пути могут иметь общие вершины. Двусвязность представляет собой более сильное условие: реберно-связный граф остается связным при удалении любого ребра, а двусвязный граф остается связным при удалении любой вершины (и всех инцидентных ей ребер). Каждый двусвязный граф является реберносвязным, однако реберно-связный граф не обязательно должен быть двусвязным. Граф, который не является двусвязным, иногда называется разделимым (separable), поскольку его можно разделить на две части, удалив лишь одну вершину. Ключом к двусвязности являются вершины разделения.
Лемма 18.7. Граф двусвязен тогда и только тогда, когда он не содержит вершин разделения (точек сочленения).
Доказательство. Предположим, что в графе имеется вершина разделения. Пусть s и t — две вершины, которые окажутся в двух различных частях графа после удаления этой вершины. Все пути, связывающие s и t, должны проходить через вершину разделения, поэтому граф не может быть двусвязным. Доказательство в обратном направлении несколько труднее и предлагается в качестве упражнения математически подготовленным читателям (см. упражнение 18.40). 
Данный граф не является двусвязным. Вершины 0, 4, 5, 6, 7 и 11 (обведены) — точки сочленения. Граф содержит пять двусвязных компонентов: один состоит из ребер 4-9, 9-11 и 4-11, другой — из ребер 7-8, 8-10 и 7-10; еще один — из ребер 0-1, 1-2, 2-6 и 6-0; следующий — из ребер 3-5 , 4-5 и 3-4; и еще имеется одиночная вершина 12. Добавление в граф ребра, соединяющего вершину 12 с вершиной 7, 8 или 10, делает граф двусвязным.
Мы уже видели, что множество ребер несвязного графа можно разбить на несколько связных подграфов, и что ребра графа, который не является реберно-связным, можно разбить на множество мостов и реберно-связных подграфов (соединенных между собой мостами). Аналогично, любой граф, который не является двусвязным, можно разбить на множество мостов и двусвязных компонентов (biconnected components), каждый из которых представляет собой двусвязный подграф. Двусвязные компоненты и мосты нельзя рассматривать как подходящее разбиение графа, поскольку точки сочленения могут входить в несколько связных компонентов (см., например, рис. 18.20). Двусвязные компоненты соединяются в точках сочленения, которые, возможно, входят в состав мостов.
Связный компонент графа обладает тем свойством, что существует путь между любыми двумя его вершинами. Аналогично, для двусвязного компонента характерно то, что между любой парой вершин существуют два непересекающихся пути.
Для определения двусвязности графа и выявления точек сочленения можно использовать тот же подход на основе DFS, что и в программе 18.7. Мы не будем рассматривать соответствующий код, поскольку он почти идентичен программе 18.7, за исключением дополнительной проверки, является ли корень дерева DFS точкой сочленения (см. упражнение 18.43). Хорошим упражнением может послужить разработка кода вывода двусвязных компонентов графа, который лишь ненамного сложнее, чем соответствующий код определения реберной связности графа (см. упражнение 18.44).
Лемма 18.8. Точки сочленения и двусвязные компоненты графа можно найти за линейное время.
Доказательство. Как и в случае леммы 18.7, этот факт непосредственно следует из того, что решения упражнений 18.43 и 18.44 добавляют в поиск в глубину лишь небольшие изменения — несколько проверок для каждого ребра, выполняемых за постоянное время. 
Понятие двусвязности представляет собой обобщение обычной связности. Возможны и дальнейшие обобщения, которые являются темой интенсивных исследований в классической теории графов и в построении алгоритмов обработки графов. Эти обобщения очерчивают рамки задач обработки графов, которые могут встретиться на практике — многие из них легко сформулировать, но совсем не легко решить.
Определение 18.4. Граф называется k-связным (k-connected), если каждую пару его вершин соединяют по меньшей мере k путей без общих вершин. Вершинная связность (vertex connectivity) графа — это минимальное количество вершин, которые нужно удалить, чтобы разделить этот граф на две части.
В этой терминологии " 1-связный " означает просто " связный " , а " 2-связный " — это то же, что и " двусвязный " . Граф с точкой сочленения обладает вершинной связностью, равной 1 (или 0), поэтому из леммы 18.7 следует, что граф 2-связен тогда и только тогда, когда значение его вершинной связности не меньше 2. Это частный случай классического результата теории графов — теоремы Уитни (Whitney’s theorem), которая гласит, что граф k-связен в том и только том случае, когда его вершинная связность не меньше k. Теорема Уитни непосредственно следует из теоремы Менгера (Menger’s theorem) (см. "Потоки в сетях" ), согласно которой минимальное количество вершин, удаление которых разъединяет две вершины в графе, равно максимальному количеству путей без общих вершин между этими двумя вершинами (для доказательства теоремы Уитни нужно применить теорему Менгера к каждой паре вершин).
Определение 18.5. Граф называется k-реберно-связным (k-edge-connected), если существуют по меньшей мере k путей без общих ребер, соединяющих каждую пару вершин графа. Реберная связность (edge connectivity) графа — это минимальное число ребер, которые нужно удалить, чтобы разделить этот граф на две части.
В этой терминологии " 2-реберно-связный " означает просто " реберно-связный " (т.е. для реберно-связного графа значение реберной связности должно быть больше 1). Другой вариант теоремы Менгера утверждает, что минимальное количество вершин в графе, удаление которых приводит к разъединению двух вершин графа, равно максимальному количеству путей без общих вершин, связывающих эти две вершины графа. Отсюда следует, что граф k-реберно-связен тогда и только тогда, когда его реберная связность равна k.
Эти определения приводят нас к обобщению задач определения связности, которые рассматривались в начале данного раздела.
st-связность. Каково минимальное количество ребер, удаление которых приведет к разъединению двух вершин s и t заданного графа? Каково минимальное количество вершин, удаление которых приведет к разъединению двух вершин s и t заданного графа?
Общая связность. Является ли заданный граф k-связным? Является ли заданный граф k-реберно-связным? Чему равны реберная связность и вершинная связность заданного графа?
Решения всех этих задач намного сложнее, чем решения простых задач связности, рассмотренных в данном разделе, но они входят в обширный класс задач обработки графов, которые можно решать с помощью универсальных алгоритмических средств, рассматриваемых в "Потоки в сетях" (конкретные решения с использованием поиска в глубину будут приведены в "Потоки в сетях" ).
Упражнения
18.33. Если граф является лесом, все его ребра являются ребрами разделения. А какие вершины являются вершинами разделения?
18.34. Рассмотрим граф
3-71-47-80-55-23-82-90-64-92-66-4.
Начертите стандартное дерево DFS для списков смежности. Найдите с его помощью мосты и реберно-связные компоненты.
18.35. Докажите, что каждая вершина любого графа принадлежит в точности одному реберно-связному компоненту.
18.36. Добавьте в программу 18.7 общедоступную функцию-член, которая позволит клиентам проверять, принадлежит ли пара заданных вершин одному и тому же реберно-связному компоненту.
18.37. Рассмотрим граф
3-71-47-80-55-23-82-90-64-92-66-4.
Начертите стандартное дерево DFS для списков смежности. Найдите с его помощью точки сочленения и двусвязные компоненты.
18.38. Выполните предыдущее упражнение, воспользовавшись стандартным деревом DFS для матрицы смежности.
18.39. Докажите, что каждое ребро графа либо является мостом, либо принадлежит в точности одному двусвязному компоненту.
18.40. Докажите, что любой граф без точек сочленения является двусвязным. Указание. Если заданы пара вершин s и t и соединяющий их путь, воспользуйтесь тем фактом, что ни одна из вершин этого пути не является точкой сочленения для построения двух непересекающихся путей, которые соединяют вершины s и t.
18.41. Напишите производный от программы 18.2 класс для определения, является ли граф двусвязным. Воспользуйтесь примитивным алгоритмом, который выполняется за время, пропорциональное V(V + E). Указание: Если перед началом поиска какая-то вершина отмечена как уже просмотренная, то это по сути удаляет ее из графа.
18.42. На основе решения упражнения 18.41 постройте класс, который определяет, является ли заданный граф 3-связным. Выведите формулу для приближенного количества просмотров каждого ребра графа в виде функции от V и E.
18.43. Докажите, что корень дерева DFS является точкой сочленения тогда и только тогда, когда у него имеется два или более (внутренних) дочерних узлов.
18.44. Пользуясь программой 18.2, напишите производный класс, который выводит двусвязные компоненты графа.
18.45. Чему равно минимальное количество ребер в любом двусвязном графе с V вершинами?
18.46. Измените программу 18.7, чтобы упростить задачу определения, является ли заданный граф реберно-связным (которая завершает работу сразу при обнаружении моста, если граф не реберно-связный), и добавьте возможность отслеживать количество просмотренных ребер. Эмпирически определите затраты для графов различных размеров, сгенерированных на основе различных моделей графов (упражнения 17.64-17.76).
18.47. Пользуясь программой 18.2, напишите производный класс, позволяющий клиентам создавать объекты, которым известны количества точек сочленения, мостов и двусвязных компонентов графа.
18.48. Эмпирически определите средние значения величин, описанных в упражнении 18.47, для графов различных размеров, сгенерированных на основе различных моделей графов (упражнения 17.64—17.76).
18.49. Определите реберную связность и вершинную связность графа
0-10-20-82-12-88-13-83-73-63-53-44-64-55-66-77-8.