|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Поразрядный поиск
В частности, в отличие от DST-деревьев, trie-деревья обладают свойством упорядоченности ключей и поэтому позволяют элементарно реализовать операции сортировать и выбрать в таблице символов (см. упражнения 15.17 и 15.18). Более того, trie-деревья столь же хорошо сбалансированы, как и DST-деревья.
Лемма 15.3. Для выполнения вставки или поиска случайного ключа в trie-дереве, построенном из N случайных (различных) битовых строк, требуется в среднем около lgN сравнений разрядов. В худшем случае количество битовых сравнений ограничено только количеством битов в искомом ключе.
К анализу trie-деревьев необходимо подходить очень внимательно в связи с требованием, что ключи должны быть различными, или, в более общем случае, что ни один ключ не должен быть префиксом другого ключа. Одна из простых моделей, соответствующая этому условию, требует, чтобы ключи были случайной (бесконечной) последовательностью разрядов, из которой выбираются разряды, необходимые для построения trie-дерева.
Тогда производительность для среднего случая можно вычислить, исходя из следующих вероятностных рассуждений. Вероятность того, что каждый из N ключей в случайном trie-дереве отличается от случайного ключа поиска по меньшей мере в одном из t ведущих разрядов, равна 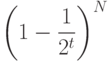 .
.
Вычитание этого значения из 1 дает вероятность того, что один из ключей в trie-дереве совпадает во всех t ведущих разрядах с ключом поиска. То есть
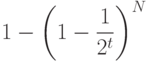 — это вероятность того, что для выполнения поиска потребуется более t сравнений разрядов. Из элементарной теории вероятностей известно, что для t > 1 сумма вероятностей того, что случайная переменная будет больше t, равна среднему значению этой случайной переменной, поэтому средние затраты на поиск определяются выражением
— это вероятность того, что для выполнения поиска потребуется более t сравнений разрядов. Из элементарной теории вероятностей известно, что для t > 1 сумма вероятностей того, что случайная переменная будет больше t, равна среднему значению этой случайной переменной, поэтому средние затраты на поиск определяются выражением 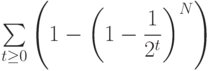
Воспользовавшись элементарной аппроксимацией 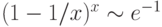 , находим, что затраты на поиск должны быть приблизительно равны
, находим, что затраты на поиск должны быть приблизительно равны 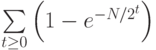
Значения приблизительно lgN членов этой суммы, для которых 2t значительно меньше N, очень близки к 1; значения всех членов, для которых 2t значительно больше N, близки к 0; и значения нескольких членов, для которых 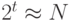 , лежат в интервале между 0 и 1. Поэтому вся сумма приблизительно равна lgN. Для более точного определения этого значения требуется выполнение очень сложных математических вычислений (см. раздел ссылок). В приведенном анализе предполагается, что значение w достаточно велико, чтобы во время поиска всегда было достаточно разрядов; но учет действительного значения w лишь уменьшит значение затрат.
, лежат в интервале между 0 и 1. Поэтому вся сумма приблизительно равна lgN. Для более точного определения этого значения требуется выполнение очень сложных математических вычислений (см. раздел ссылок). В приведенном анализе предполагается, что значение w достаточно велико, чтобы во время поиска всегда было достаточно разрядов; но учет действительного значения w лишь уменьшит значение затрат.
В худшем случае можно получить два ключа с очень большим количеством одинаковых разрядов, но вероятность подобного события ничтожно мала. Вероятность того, что результат для худшего случая из леммы 15.3 не соблюдается, экспоненциально мала (см. упражнение 15.29). 
Еще один подход к анализу trie-деревьев заключается в обобщении способа анализа BST-деревьев (см. лемму 12.6). Вероятность того, что к ключей начинаются с бита 0, а N — k ключей начинаются с бита 1, равна
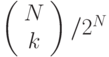
 .
.
Это рекуррентное соотношение похоже на рекуррентное соотношение для быстрой сортировки, которое было решено в "Быстрая сортировка" , но решить его значительно труднее. Как ни удивительно, решением является выражение для средних затрат на поиск, полученное на основании леммы 15.3, умноженное в точности на N (см. упражнение 15.26). Исследование самого рекуррентного соотношения позволяет понять, почему trie-деревья лучше сбалансированы, чем BST-деревья: вероятность того, что разбиение произойдет вблизи середины дерева, гораздо выше, чем для любого другого места. Поэтому это рекуррентное соотношение больше напоминает соотношение для сортировки слиянием (приблизительное решение которого равно NlgN), чем соотношение для быстрой сортировки (приблизительное решение 2NlgN).
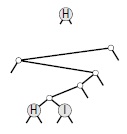
Неприятное свойство trie-деревьев, также отличающее их от других рассмотренных типов деревьев поиска — однонаправленные пути для ключей с одинаковыми разрядами. Например, ключи, которые различаются только в последнем разряде, всегда требуют пути, длина которого равна длине ключа, независимо от количества ключей в дереве (см. рис. 15.8). Количество внутренних узлов может быть даже больше, чем количество ключей.
На этих рисунках показан результат вставки ключей H = 01000 и I = 01001 в первоначально пустое trie-дерево. Как и в DST-дереве (см. рис. 15.4), длина пути ограничена длиной двоичного представления ключей; однако, как видно из этого примера, пути могут иметь такую длину даже при наличии в trie-дереве всего двух ключей.
Лемма 15.4. Trie-дерево, построенное из N случайных w-разрядных ключей, содержит в среднем около 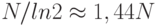 узлов.
узлов.
Изменив рассуждения в лемме 15.3, можно записать выражение для среднего количества узлов в trie-дереве с N ключами (см. упражнение 15.27):
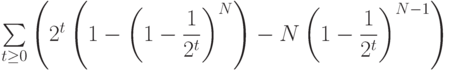 .
.
Математический анализ, позволяющий получить приблизительное значение указанной в свойстве суммы, значительно сложнее, чем приведенный для леммы 15.3, т.к. значения многих слагаемых не равны 0 или 1 (см. раздел ссылок). 
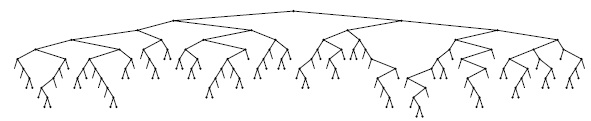
Полученные результаты можно проверить эмпирически. Например, на рис. 15.9 показано большое дерево, имеющее на 44% больше узлов, чем BST-дерево или DST-дерево, построенное из этого же множества ключей. Тем не менее, оно хорошо сбалансировано, и затраты на поиск в нем почти оптимальны.
Это trie-дерево, построенное в результате вставки около 200 случайных ключей, хорошо сбалансировано, но из-за однонаправленного ветвления содержит на 44 процента больше узлов, чем было бы необходимо в ином случае. (Пустые ссылки в листьях не показаны.)
На первый взгляд может показаться, что дополнительные узлы приведут к существенному повышению средних затрат на поиск, но в действительности это не так: например, при удвоении количества узлов в сбалансированном trie-дереве средние затраты на поиск увеличатся всего на 1 (сравнение разрядов — прим. перев.).
Для удобства реализации в программах 15.2 и 15.3 предполагалось, что ключи различны и имеют фиксированную длину — чтобы иметь уверенность, что рано или поздно ключи окажутся различными, а программы смогут провести побитовую обработку и никогда не выйдут за границу ключей. Для удобства анализа в леммах 15.2 и 15.3 также неявно предполагалось, что ключи имеют произвольное количество разрядов, чтобы в конце концов, если пренебречь очень малой (экспоненциально убывающей) вероятностью, они оказывались различными. Прямым следствием этого допущения является то, что и программы, и их анализ применимы также для ключей, являющихся битовыми строками переменной длины, хотя здесь требуется нескольких уточнений.
Для использования программ в приведенном виде с ключами переменной длины нужно расширить ограничение различия ключей: ни один из ключей не должен быть префиксом другого ключа. Как будет показано в разделе 15.5, в некоторых приложениях это ограничение достигается автоматически. В противном случае такие ключи можно обрабатывать, сохраняя информацию во внутренних узлах, поскольку каждый обрабатываемый префикс соответствует какому-либо внутреннему узлу в trie-дереве (см. упражнение 15.31).
Для достаточно длинных ключей, состоящих из случайных разрядов, утверждения для среднего случая, приведенные в леммах 15.2 и 15.3, по-прежнему справедливы. В худшем случае высота trie-дерева по-прежнему ограничена количеством разрядов в самых длинных ключах. Эти затраты могут оказаться весьма существенными, если ключи имеют очень большую длину и, возможно, некоторое сходство, что вполне может быть в случае закодированных символьных данных. В следующих двух разделах рассматриваются методы снижения затрат в trie-деревьях с длинными ключами. Один из способов сокращения путей в trie-деревьях — свертывание однонаправленных ветвей в единые ссылки (изящный и эффективный метод выполнения этой задачи будет приведен в разделе 15.3). Другой способ уменьшения длин путей в trie-деревьях допускает существование более двух ссылок для каждого узла; этот подход является темой раздела 15.4.
Упражнения
15.11. Нарисуйте результат вставки элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое trie-дерево.
15.12. Что происходит, если программа 15.3 применяется для вставки записи, ключ которой равен какому-либо ключу, уже присутствующему в trie-дереве?
15.13. Нарисуйте результат вставки элементов с ключами 01010011 00000111 00100001 01010001 11101100 00100001 10010101 01001010 в первоначально пустое trie-дерево.
15.14. Эмпирически сравните высоту, количество узлов и длину внутреннего пути trie-дерева, построенного вставками N случайных 32-разрядных ключей в первоначально пустое дерево, с этими же характеристиками стандартного BST-дерева и RB-дерева ( "Сбалансированные деревья" ), построенных из тех же ключей, для N = 103, 104, 105 и 106 (см. упражнение 15.6).
15.15. Приведите полную характеристику длины внутреннего пути для худшего случая trie-дерева, содержащего N различных w-разрядных ключей.
15.16. Реализуйте операцию удалить для реализации таблицы символов на основе trie-дерева.
15.17. Реализуйте операцию выбрать для реализации таблицы символов на основе trie-дерева.
15.18. Реализуйте операцию сортировать для реализации таблицы символов на основе trie-дерева.
15.19. Напишите программу, которая выводит все ключи trie-дерева, имеющие те же начальные t разрядов, что и заданный ключ.
15.20. Воспользуйтесь конструкцией union языка C++ для реализации операций найти и вставить на основе trie-деревьев с не листовыми узлами, которые содержат ссылки, но не содержат элементы, и с листьями, которые содержат элементы, но не содержат ссылки.
15.21. Воспользуйтесь парой производных классов для реализации операций найти и вставить на основе trie-деревьев с не листовыми узлами, которые содержат ссылки, но не содержат элементы, и с листьями, которые содержат элементы, но не содержат ссылки.
15.22. Измените программы 15.3 и 15.2 так, чтобы ключ поиска хранился в машинном регистре и при спуске по trie-дереву на уровень вниз для выборки следующего разряда выполнялся сдвиг на один разряд.
15.23. Измените программы 15.3 и 15.2 так, чтобы они использовали таблицу из 2r trie-деревьев для фиксированной константы r. Первые r разрядов ключа должны использоваться для индексации в таблице, а по остальным разрядам ключа должны применяться стандартные алгоритмы доступа в trie-дереве. Это изменение позволяет сэкономить около r шагов, если только таблица не содержит большого количества пустых записей.
15.24. Какое значение r нужно выбрать в упражнении 15.23 при наличии N случайных ключей (которые достаточно длинны, чтобы их можно было считать различными)?
15.25. Напишите программу для вычисления количества узлов в trie-дереве, соответствующих данному множеству различных ключей фиксированной длины, с помощью их сортировки и сравнения соседних ключей в отсортированном списке.
15.26. Докажите по индукции, что 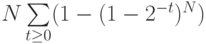 — это решение рекуррентного соотношения наподобие быстрой сортировки, приведенного после леммы 15.3, для длины внешнего пути в случайном trie-дереве.
— это решение рекуррентного соотношения наподобие быстрой сортировки, приведенного после леммы 15.3, для длины внешнего пути в случайном trie-дереве.
15.27. Получите выражение, приведенное в лемме 15.4 для среднего количества узлов в случайном trie-дереве.
15.28. Напишите программу для вычисления среднего количества узлов в случайном trie-дереве, состоящем из N узлов, и вывода этого значения с точностью до 10-3, для N = 103, 104, 105 и 106 .
15.29. Докажите, что высота trie-дерева, построенного из N случайных битовых строк, приблизительно равна 2 lgN. Совет: воспользуйтесь решением задачи о дне рождения (см. лемму 14.2).
15.30. Докажите, что средние затраты на поиск в DST-дереве, построенном из случайных ключей, асимптотически равны lgN (см. леммы 15.1 и 15.2).
15.31. Измените программы 15.2 и 15.3 так, чтобы они обрабатывали битовые строки переменной длины с единственным ограничением: в структуре данных не должны храниться записи с повторяющимися ключами. В частности, решите, какое значение возвращать при вызове bit(v, d) для случая, когда d больше длины v.
15.32. Воспользуйтесь trie-деревом для построения структуры данных, которая может поддерживать АТД таблицы существования для w-разрядных целых чисел. Программа должна поддерживать операции создать, вставить и найти при условии, что вставить и найти принимают целочисленные аргументы, а найти возвращает nullItem.key() при неудачном поиске и полученный аргумент в случае успешного поиска.