Хеширование

Динамические хеш-таблицы

С увеличением количества ключей в хеш-таблице скорость поиска снижается. При использовании цепочек переполнения время поиска увеличивается постепенно: если количество ключей в таблице удваивается, то и время поиска удваивается. Это же справедливо и для разреженных таблиц по отношению к таким методам с открытой адресацией, как линейное опробование и двойное хеширование, но по мере заполнения таблицы затраты существенно возрастают и, что гораздо хуже, наступает момент, когда невозможно вставить ни один ключ. Эта ситуация отличается от деревьев поиска, в которых рост происходит естественным образом. Например, в RB-дереве при каждом удвоении количества узлов затраты на поиск возрастают совсем ненамного (на одно сравнение).

Один из способов расширения хеш-таблиц — удвоение размера таблицы, когда она начинает заполняться. Удвоение размера таблицы — дорогостоящая операция, поскольку все элементы в таблице должны быть вставлены повторно, однако она выполняется нечасто. Программа 14.7 является реализацией увеличения таблицы с линейным опробованием путем ее удвоения. Пример таких удвоений показан на рис. 14.12.

Программа 14.7. Динамическая вставка в хеш-таблицу (для линейного опробования)

Данная реализация операции insert для линейного опробования (см. программу 14.4) обрабатывает произвольное количество ключей, удваивая размер таблицы при каждом заполнении таблицы наполовину (этот же подход может быть использован для двойного хеширования или цепочек переполнения). Удвоение требует распределения памяти для новой таблицы и повторного хеширования в нее всех ключей, а затем освобождения памяти, занимаемой старой таблицей. Функция-член init используется для построения или повторного построения таблицы, заполненной пустыми элементами указанных размеров; она реализована так же, как конструктор ST в программе 14.4, поэтому ее код опущен.

  private:
    void expand()
      { Item *t = st;
        init(M+M);
        for (int i = 0; i < M/2; i++)
          if (!t[i].null()) insert(t[i]);
        delete t;
      }
  public:
    ST(int maxN)
      { init(4); }
    void insert(Item item)
      { int i = hash(item.key(), M);
        while (!st[i].null()) i = (i+1) % M;
        st[i] = item;
        if (N++ >= M/2) expand();
      }
      

Рис. 14.12. Динамическое расширение хеш-таблицы

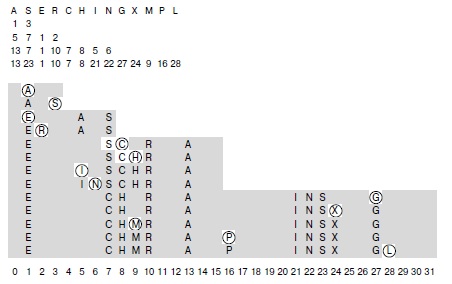
На этой диаграмме показан процесс вставки ключей A S E R C H I N G X M P L в динамическую хеш-таблицу, которая расширяется удвоением размера, с использованием хеш-значений, приведенных вверху, и разрешением коллизий с помощью линейного опробования. В четырех строках под ключами приводятся хеш-значения для размеров таблицы, равных 4, 8, 16 и 32. Начальный размер таблицы равен 4, затем, перед вставкой E, он удваивается до 8, перед вставкой C — до 16 и перед вставкой G — до 32. При каждом удвоении размера таблицы для всех ключей выполняются повторные хеширование и вставка. Все вставки выполняются в разреженные таблицы (заполненные менее чем на одну четверть для повторной вставки и от четверти до половины в остальных случаях), поэтому коллизий возникает мало.

Это же решение работает и для двойного хеширования, а основная идея применима и для цепочек переполнения (см. упражнение 14.46). Каждый раз, когда таблица заполняется более чем наполовину, она расширяется путем удвоения ее размера. После первого расширения степень заполнения таблицы всегда составляет от одной четвертой до одной второй, поэтому средние затраты на поиск составляют менее трех проб. И хотя операция повторного построения таблицы является дорогостоящей, она выполняется столь редко, что ее стоимость составляет лишь постоянную долю общих затрат на построение таблицы.

Эту концепцию можно выразить и по-другому, сказав, что средние затраты на одну вставку составляют меньше четырех проб. Это утверждение не равносильно утверждению, что для каждой вставки требуется менее четырех проб; и действительно, мы знаем, что вставки, которые приводят к удвоению размера таблицы, требуют большого количества проб. Это рассуждение — простой пример амортизационного анализа: нельзя гарантировать быстрое выполнение каждой операции этого алгоритма, но можно гарантировать, что будут низкими средние затраты на одну операцию.

Хотя общие затраты низки, профиль производительности вставок неравномерен: большинство операций выполняется исключительно быстро, но иногда для некоторых операций требуется почти столько же времени, сколько ранее было затрачено на построение всей таблицы. При увеличении размера таблицы от 1 тысячи до 1 миллиона ключей это замедление может случиться около 10 раз. Такое поведение приемлемо во многих приложениях, но может оказаться недопустимым, если желательны или обязательны абсолютные гарантии производительности. Например, если банк или авиакомпания могут допустить, что 10 из миллиона клиентов будут ожидать длительное время, то в таких приложениях, как онлайновая система обработки финансовых транзакций или система управления авиаполетами, долгое ожидание может повлечь катастрофические последствия.

При поддержке операции АТД удалить может иметь смысл сжимать таблицу, уменьшая вдвое ее размер при уменьшении количества ее ключей (см. упражнение 14.44). Но здесь требуется выполнение одного условия: границы уменьшения должны отличаться от границ увеличения, поскольку иначе небольшое количество операций вставить и удалить может привести даже для очень больших таблиц к серии операций увеличения и уменьшения размера вдвое.

Рис. 14.13. Динамическое хеширование

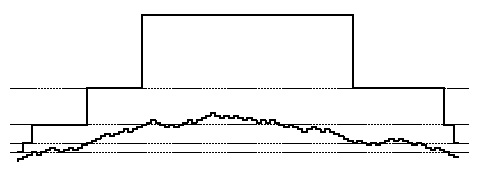
На данной диаграмме показано количество ключей в таблице (внизу) и размер таблицы (вверху) при вставках и удалениях ключей в динамической хеш-таблице, использующей следующий алгоритм:размер таблицы удваивается при заполнении ее наполовину и уменьшается в два раза, если заполненной остается лишь одна восьмая часть. Размер таблицы вначале равен 4 и всегда равен степени 2 (пунктирные линии на рисунке соответствуют степеням 2). Размер таблицы меняется тогда, когда кривая, отображающая количество ключей в таблице, пересекает пунктирную линию в первый раз после пересечения другой пунктирной линии. Доля заполнения таблицы всегда равна от одной четверти до одной восьмой.

Этот метод годится для использования в реализации таблицы символов, предназначенной для библиотеки программ общего назначения, когда последовательности операций непредсказуемы, поскольку позволяет приемлемым образом обрабатывать таблицы любых размеров. Основной его недостаток — затраты на повторное хеширование и распределение памяти при увеличении и уменьшении таблицы. В типичном случае, когда чаще выполняются операции поиска, гарантированная разреженность таблицы обеспечивает прекрасную производительность. В "Внешний поиск" будет рассмотрен другой подход, позволяющий избежать повторного хеширования и подходящий для очень больших таблиц внешнего поиска.

Упражнения

14.40. Приведите содержимое хеш-таблицы, образованной вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустую таблицу с начальным размером М = 4, которая удваивает размер при заполнении наполовину, с разрешением коллизий методом линейного опробования. Для преобразования k-ой буквы алфавита в индекс таблицы воспользуйтесь хеш-функцией 11k mod М.

14.41. Будет ли более экономичным увеличивать хеш-таблицу, утраивая (а не удваивая) ее размер при заполнении таблицы наполовину?

14.42. Будет ли более экономичным увеличивать хеш-таблицу, утраивая ее размер при заполнении таблицы на одну треть (вместо удвоения при заполнении наполовину)?

14.43. Будет ли более экономичным увеличивать хеш-таблицу, удваивая ее размер при заполнении таблицы на три четверти (а не наполовину)?

14.44. Добавьте в программу 14.7 функцию удалить, которая удаляет элемент, как в программе 14.4, но затем сжимает таблицу, вдвое уменьшая ее размер, если после удаления таблица остается пустой на семь восьмых.

14.45. Реализуйте версию программы 14.7 для цепочек переполнения, которая в 10 раз увеличивает размер таблицы каждый раз, когда средняя длина списка становится равной 10.

14.46. Измените программу 14.7 и реализацию из упражнения 14.44, чтобы в них использовалось двойное хеширование с " ленивым " удалением (см. упражнение 14.33). Нужно, чтобы программа подсчитывала количество фиктивных объектов и пустых позиций для принятия решения о необходимости расширения или сужения таблицы.

14.47. Разработайте реализацию таблицы символов с использованием линейного опробования в динамических таблицах, которая содержит деструктор, конструктор копирования и перегруженную операцию присваивания и поддерживает операции АТД первого класса таблицы символов создать, подсчитать, найти, вставить, удалить и объединить при поддержке клиентских дескрипторов (см. упражнения 12.6 и 12.7).