Хеширование

В конкретном приложении универсальное хеширование может работать значительно медленнее, чем более простые методы, поскольку при наличии длинных ключей выполнение двух арифметических операций для каждого символа в ключе может потребовать слишком много времени. Для обхода этого ограничения ключи можно обрабатывать большими фрагментами. Действительно, можно использовать наибольшие фрагменты, которые помещаются в машинное слово, так же, как и в случае с элементарным модульным хешированием. Как уже подробно обсуждалось ранее, в некоторых строго типизованных языках высокого уровня подобная операция может оказаться труднореализуемой или требовать специальных вывертов, но в C++ она может не требовать больших затрат или вовсе ничего не требовать, если использовать приведение к подходящим форматам представления данных. Во многих ситуациях эти факторы важно учитывать, поскольку вычисление хеш-функции может выполняться во внутреннем цикле — следовательно, ускорив хеш-функцию, можно ускорить все вычисление.

Несмотря на очевидные преимущества рассмотренных методов, их реализация требует внимания по двум причинам. Во-первых, необходимо быть внимательным во избежание ошибок при преобразовании типов и использовании арифметических функций для различных машинных представлений ключей.

Программа 14.2. Универсальная хеш-функция (для строковых ключей)

Эта программа выполняет те же вычисления, что и программа 14.1, однако для аппроксимации вероятности возникновения конфликтов для двух несовпадающих ключей до значения 1/M вместо фиксированных оснований системы счисления применяются псевдослучайные значения коэффициентов. Для минимизации нежелательных затрат времени при вычислении хеш-функции используется грубый генератор случайных чисел.

  int hashU(char *v, int M)
    { int h, a = 31415, b = 27183;
      for (h = 0; *v != 0; v++, a = a*b % (M-1))
        h = (a*h + *v) % M;
      return (h < 0) ? (h + M) : h;
    }
      

Такие операции часто являются источниками ошибок, особенно при переносе программы со старого компьютера на новый, с другим количеством разрядов в слове или прочими отличиями в точности выполнения операций. Во-вторых, весьма вероятно, что во многих приложениях вычисление хеш-функции будет выполняться во внутреннем цикле, и время ее выполнения может в значительной степени определять общее время выполнения. В подобных случаях важно убедиться, что функция сводится к эффективному машинному коду. Подобные операции — известные источники неэффективности; например, разница во времени выполнения простого модульного метода для целых чисел и версии, в которой вначале выполняется умножение ключа на 0,61616, может быть существенной. Наиболее быстрый метод для многих компьютеров — принять M равным степени 2 и воспользоваться хеш-функцией

  inline int hash(Key v, int M)
    { return v & (M-1); }
      

Эта функция использует только lg M — 1 младших разрядов ключей. Для устранения нежелательных эффектов плохого распределения ключей можно применять операцию побитового " И " , которая выполняется существенно быстрее и проще, чем другие операции.

Типичная ошибка в реализациях хеширования заключается в том, что хеш-функция всегда возвращает одно и то же значение — возможно, из-за неправильного выполнения требуемого преобразования типов. Такая ошибка называется ошибкой производительности, поскольку использующая такой метод хеширования программа вполне может выполняться корректно, но крайне медленно (т.к. ее эффективная работа возможна только при равномерном распределении хеш-значений). Однострочные реализации этих функций очень легко тестировать, поэтому настоятельно рекомендуется проверять, насколько успешно они работают для типов ключей, которые ожидаются в любой конкретной реализации таблицы символов.

Для проверки гипотезы, что хеш-функция создает случайные значения, можно использовать критерий 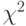(см. упражнение 14.5), но, возможно, это требование слишком жесткое. Вообще вполне достаточно, если метод хеширования выдает каждое значение одинаковое количество раз — такое поведение соответствует значению %2, равному 0, и совсем не является случайным. Однако следует с подозрением относиться и к очень большим значениям %2. На практике, вероятно, достаточно проверить, что значения распределены так, что ни одно из них не доминирует (см. упражнение 14.15). По этим же соображениям хорошо разработанная реализация таблицы символов, основанная на универсальном хешировании, могла бы периодически проверять, являются ли хеш-значения равномерно распределенными. А клиентскую программу можно информировать о том, что имело место либо маловероятное событие, либо ошибка в хеш-функции. Подобного рода проверка оказалась бы разумным дополнением к любому реальному рандомизированному алгоритму.

Упражнения

14.1. Используя абстракцию digit из "Поразрядная сортировка" для обработки машинного слова как последовательности байтов, реализуйте рандомизированный метод хеширования для ключей, представленных битами в машинных словах.

14.2. Проверьте, требуется ли время на преобразование 4-байтового ключа в 32-разрядное целое число в используемой вами программной среде.

о 14.3. Разработайте функцию хеширования для строковых ключей, основанную на идее одновременной загрузки 4 байтов с последующим выполнением арифметических операций сразу над 32 битами. Сравните время выполнения этой функции с временем выполнения программы 14.1 для 4-, 8-, 16- и 32-байтовых ключей.

14.4. Напишите программу для определения значений а и M при минимально возможном значении M, чтобы хеш-функция a*x % M выдавала различные (несовпадающие) значения для ключей, представленных на рис. 14.2. Полученный результат является примером совершенной хеш-функции.

о 14.5. Напишите программу для вычисления критерия 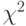для хеш-значений N ключей при размере таблицы, равном M. Это число определяется равенством

14.6. Воспользуйтесь программой из упражнения 14.5 для вычисления хеш-функции 618033*x % 10000 для ключей, которые являются случайными положительными целыми числами, меньшими 10⁶.

14.7. Воспользуйтесь программой из упражнения 14.5 для вычисления хеш-функции из программы 14.1 для различных строковых ключей, полученных из какого-либо большого файла в вашей системе, например, словаря.

14.8. Пусть ключи являются t-разрядными двоичными целыми числами. Для модульной хеш-функции с простым основанием M докажите, что каждый бит ключа обладает тем свойством, что существуют два ключа с различными хеш-значениями, отличающиеся только этим битом.

14.9. Рассмотрите идею реализации модульного хеширования для целочисленных ключей с помощью выражения (a*x) % M, где а — произвольное фиксированное простое число. Приводит ли это изменение к достаточному перемешиванию разрядов, чтобы можно было использовать не простое значение M?

14.10. Докажите, что (((ax) mod M) + b) mod M = (ax + b) mod M, при условии, что a, b, x и M — неотрицательные целые числа.

14.11. Если в упражнении 14.7 использовать слова из текстового файла, например книги, то вряд ли удастся получить хороший критерий 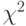. Объясните, почему это так.

14.12. Воспользуйтесь программой из упражнения 14.5 для вычисления хеш-функции 97*x % M для всех размеров таблицы в диапазоне от 100 до 200, используя в качестве ключей 10³ случайных положительных целых чисел, меньших 10⁶.

14.13. Воспользуйтесь программой из упражнения 14.5 для вычисления хеш-функции 97*x % M для всех размеров таблицы в диапазоне от 100 до 200, используя в качестве ключей целые числа в диапазоне от 10² до 10³.

14.14. Воспользуйтесь программой из упражнения 14.5 для вычисления хеш-функции 100*x % M для всех размеров таблицы в диапазоне от 100 до 200, используя в качестве ключей 10³ случайных положительных целых чисел, меньших 10⁶.

14.15. Выполните упражнения 14.12 и 14.14, но используйте более простой критерий отбрасывания хеш-функций, которые выдают любое значение более 3N/ M раз.