|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Введение
Программа 1.2 — реализация операций объединение и поиск, образующих алгоритм быстрого объединения для решения задачи связности. Похоже, что алгоритм быстрого объединения работает быстрее алгоритма быстрого поиска, поскольку для каждой вводимой пары ему не нужно просматривать весь массив; но насколько быстрее? В данном случае ответить на этот вопрос труднее, чем в случае быстрого поиска, поскольку время выполнения в большей степени зависит от характера входных данных. Выполнив экспериментальные исследования или математический анализ (см. "Принципы анализа алгоритмов" ), можно показать, что программа 1.2 значительно эффективнее программы 1.1, и ее можно использовать для решения очень сложных реальных задач. Одно из таких экспериментальных исследований будет рассмотрено в конце этого раздела. А пока быстрое объединение можно считать усовершенствованием, поскольку оно устраняет основной недостаток алгоритма быстрого поиска (тот факт, что для выполнения M операций объединение между N объектами программе требуется выполнение, по меньшей мере, N M инструкций).
Программа 1.2. Решение задачи связности методом быстрого объединения
Если тело цикла while в программе 1.1 заменить этим кодом, мы получим программу, которая соответствует тем же спецификациям, что и программа 1.1, но выполняет меньше вычислений для операции объединение за счет выполнения большего количества вычислений для операции поиск. Циклы for и последующий оператор if в этом коде определяют необходимые и достаточные условия связности p и q в массиве id. Оператор присваивания id[i] = j реализует операцию объединение.
for (i = p; i != id[i]; i = id[i]) ;
for (j = q; j != id[j]; j = id[j]) ;
if (i == j) continue;
id[i] = j;
cout << " " << p << " " << q << endl;
Это различие между быстрым объединением и быстрым поиском действительно повышает производительность, однако у быстрого объединения есть недостаток: нельзя гарантировать, что оно будет выполняться существенно быстрее быстрого поиска в каждом случае, поскольку характер входных данных может замедлить операцию поиск.
Лемма 1.2. Для M пар из N объектов, когда M > N , решение задачи связности алгоритмом быстрого объединения может потребовать выполнения более чем MN/2 инструкций.
Предположим, что пары вводятся в следующем порядке: 1-2, 2-3, 3-4 и т.д. После ввода N — 1 таких пар мы получим N объектов, принадлежащих к одному множеству, а сформированное алгоритмом быстрого объединения дерево представляет собой прямую линию, где объект N указывает на объект N — 1 , тот, в свою очередь, — на объект N — 2, тот — на N — 3 и т.д. Чтобы выполнить операцию поиск для объекта N, программа должна перейти по N — 1 указателям. Таким образом, среднее количество указателей, по которым выполняются переходы для первых N пар, равно
(0 + 1 +...+ (N - 1))/N = (N-1)/2
Теперь предположим, что все остальные пары связывают объект N с каким-либо другим объектом. Чтобы выполнить операцию поиск для каждой из этих пар, требуется перейти, по меньшей мере, по (N - 1) указателям. Общий итог для M операций поиск при такой последовательности вводимых пар определенно больше M N/2. 
К счастью, можно легко модифицировать алгоритм, чтобы худшие случаи, подобные этому, гарантированно не имели места. При выполнении операции объединение можно не произвольным образом соединять второе дерево с первым, а отслеживать количество узлов в каждом дереве и всегда соединять меньшее дерево с большим. Это изменение требует несколько более объемного кода и наличия еще одного массива для хранения счетчиков узлов, как показано в программе 1.3, но оно ведет к существенному повышению эффективности. Мы будем называть этот алгоритм алгоритмом взвешенного быстрого объединения (weighted quick-union algorithm).
Программа 1.3. Взвешенная версия быстрого объединения
Эта программа — модификация алгоритма быстрого объединения (см. программу 1.2), которая в служебных целях для каждого объекта, у которого id[i] == i, поддерживает дополнительный массив sz, где хранятся количества узлов в соответствующих деревьях, чтобы операция объединение могла связывать меньшее из двух указанных деревьев с большим, тем самым предотвращая разрастание длинных путей в деревьях.
#include <iostream.h>
static const int N = 10000;
int main() {
int i, j, p, q, id[N], sz[N];
for (i = 0; i < N; i++) {
id[i] = i; sz[i] = 1;
}
while ( cin >> p >> q) {
for (i = p; i != id[i]; i = id[i]) ;
for (j = q; j != id[j]; j = id[j]) ; if (i == j) continue;
if (sz[i] < sz[j]) {
id[i] = j; sz[j] += sz[i];
} else {
id[j] = i; sz[i] += sz[j];
}
cout << " " << p << " " << q << endl;
}
}
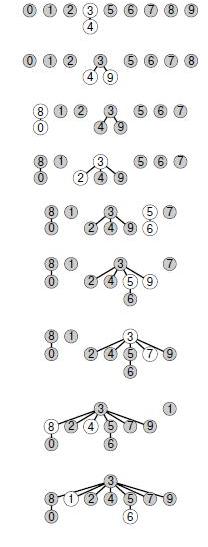
На рис. 1.7 показан лес деревьев, созданных алгоритмом взвешенного поиска для примера входных данных с рис. 1.1. Даже в этом небольшом примере пути в деревьях существенно короче, чем в случае невзвешенной версии, приведенной на рис. 1.5.
На рис. 1.8 демонстрируется, что происходит в худшем случае, когда размеры наборов, которые должны быть объединены в операции объединение, всегда равны (и являются степенью 2). Эти структуры деревьев выглядят сложными, но у них есть простое свойство: максимальное количество указателей, по которым необходимо перейти, чтобы добраться до корня в дереве, состоящем из 2n узлов, равно п. При слиянии двух деревьев, состоящих из 2n узлов, получается дерево, состоящее из 2n+1 узлов, а максимальное расстояние до корня увеличивается до п + 1. Это наблюдение можно обобщить для доказательства того, что взвешенный алгоритм значительно эффективнее невзвешенного.
Лемма 1.3. Для определения того, связаны ли два из N объектов, алгоритм взвешенного быстрого объединения переходит максимум по log N указателям.
Можно доказать, что для операции объединение сохраняется свойство, что количество указателей, проходимых из любого узла до корня в множестве к объектов, не превышает log к. При объединении набора, состоящего из i узлов, с набором, состоящим из j узлов, при  количество указателей, которые должны отслеживаться в меньшем наборе, увеличивается на 1, но теперь узлы находятся в наборе размера i + j, и свойство остается справедливым, поскольку
количество указателей, которые должны отслеживаться в меньшем наборе, увеличивается на 1, но теперь узлы находятся в наборе размера i + j, и свойство остается справедливым, поскольку 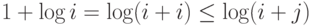 .
. 
На этой последовательности рисунков демонстрируется результат изменения алгоритма быстрого объединения, когда корень меньшего из двух деревьев связывается с корнем большего. Расстояние от каждого узла до корня его дерева невелико, поэтому операция поиска выполняется эффективно.
Наихудшая ситуация для алгоритма взвешенного быстрого объединения — когда каждая операция объединения связывает деревья одинакового размера. Если количество объектов меньше 2n, расстояние от любого узла до корня его дерева меньше п.
Практическая польза леммы 1.3 заключается в том, что количество инструкций, которые алгоритм взвешенного быстрого объединения использует для обработки M ребер между N объектами, не превышает Mlog N, умноженного на некоторую константу (см. упражнение 1.9). Этот вывод резко отличается от вывода, что алгоритм быстрого поиска всегда (а алгоритм быстрого объединения иногда) использует не менее M N/ 2 инструкций. Таким образом, при использовании взвешенного быстрого объединения можно гарантировать решение очень сложных встречающихся на практике задач за приемлемое время (см. упражнение 1.11). Ценой добавления нескольких дополнительных строк кода мы получаем программу, которая при решении очень сложных задач, которые могут встретиться на практике, работает буквально в миллионы раз быстрее, чем более простые алгоритмы.
Из приведенных диаграмм видно, что лишь сравнительно небольшое количество узлов располагаются далеко от корня; действительно, экспериментальное изучение очень сложных задач показывает, что, как правило, для решения практических задач посредством использования алгоритма взвешенного быстрого объединения, реализованного в программе 1.3, требуется линейное время. То есть затраты времени на выполнение алгоритма равны затратам времени на считывание входных данных с постоянным коэффициентом. Вряд ли можно было бы рассчитывать найти более эффективный алгоритм.
Тут же возникает вопрос: можно ли найти алгоритм, обеспечивающий гарантированную линейную производительность. Этот вопрос — исключительно трудный, который уже много лет не дает покоя исследователям (см. "Принципы анализа алгоритмов" ). Существует множество способов дальнейшего совершенствования алгоритма взвешенного быстрого объединения. В идеале было бы желательно, чтобы каждый узел указывал непосредственно на корень своего дерева, но не хотелось бы расплачиваться за это изменением большого количества указателей, как в алгоритме быстрого объединения. К идеалу можно приблизиться, просто делая все проверяемые узлы указывающими на корень. На первый взгляд этот шаг кажется весьма радикальным, но его легко реализовать, а в структуре этих деревьев нет ничего неприкосновенного, и если их можно изменить, чтобы сделать алгоритм более эффективным, то так и следует сделать. Этот метод, названный сжатием пути (path compression), можно легко реализовать, добавляя еще один проход по каждому пути во время выполнения операции объединение и занося в элемент id, соответствующий каждой встреченной вершине, указатель на корень. В результате деревья становятся почти совершенно плоскими, приближаясь к идеалу, обеспечиваемому алгоритмом быстрого поиска (см. рис. 1.9). Анализ, устанавливающий этот факт, исключительно сложен, но сам метод прост и эффективен. Результат сжатия пути для большого примера показан на рис. 1.11.
Существует множество других способов реализации сжатия пути. Например, программа 1.4 представляет собой реализацию, которая сжимает пути, сдвигая каждую ссылку на следующий узел в пути вверх по дереву (см. рис. 1.10). Этот метод несколько проще реализовать, чем полное сжатие пути (см. упражнение 1.16), но он дает тот же конечный результат. Мы называем этот вариант взвешенным быстрым объединением со сжатием пути делением пополам (weighted quick-union with path compression by halving). Какой из этих методов эффективнее? Оправдывает ли достигаемая экономия время, требующееся для реализации сжатия пути? Существует ли какая-либо иная технология, применение которой следовало бы рассмотреть? Чтобы ответить на эти вопросы, следует внимательнее рассмотреть алгоритмы и их реализации. Мы вернемся к этой теме в "Принципы анализа алгоритмов" в контексте рассмотрения основных подходов к анализам алгоритмов.
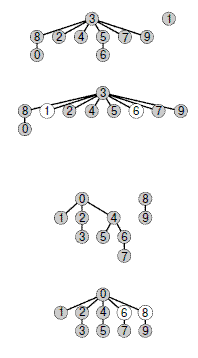
Пути в деревьях можно сделать еще короче, просто занося во все просматриваемые объекты указатели на корень нового дерева во время операции объединения, как показано в этих двух примерах. В примере на верхнем рисунке показан результат, соответствующий рис. 1.7. В случае коротких путей сжатие пути не оказывает никакого влияния, но после обработки пары 1 6 узлы 1, 5 и 6 указывают на узел 3, в результате чего дерево становится более плоским, чем на рис. 1.7. В примере на нижнем рисунке показан результат, соответствующий рис. 1.8. В деревьях могут появляться пути, которые содержат больше одной-двух связей, но при каждом прохождении они становятся более плоскими. В данном случае после обработки пары 6 8 дерево становится более плоским, а узлы 4, 6 и 8 указывают на узел 0.
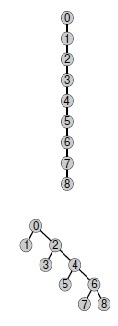
Можно уменьшить длину путей вверх по дереву почти вдвое, беря сразу по две ссылки и занося в нижнюю из них указатель на тот же узел, что и в верхней, как показано в этом примере. Конечный результат выполнения такой операции для каждого проходимого пути приближается к результату, получаемому в результате полного сжатия пути.
Здесь отображен результат обработки случайных пар из 100 объектов алгоритмом взвешенного быстрого объединения со сжатием пути. Все узлы этого дерева, кроме двух, находятся на расстоянии одного-двух шагов от корня.