|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Введение
Алгоритмы объединения и поиска
Первый шаг в процессе разработки эффективного алгоритма решения данной задачи — реализация простого алгоритма ее решения. Если нужно решить несколько вариантов конкретной задачи, которые оказываются простыми, это может быть выполнено посредством простой реализации. Если требуется более сложный алгоритм, то простая реализация предоставляет возможность проверить правильность работы алгоритма для простых случаев и может служить базовым замером для оценки характеристик производительности. Эффективность важна всегда, но при разработке первой программы решения задачи в первую очередь необходимо убедиться в том, что программа обеспечивает правильное решение.
Первое, что приходит в голову — организовать способ сохранения всех вводимых пар, а затем создать функцию для их просмотра, чтобы попытаться выяснить, связана ли очередная пара объектов. Однако мы используем другой подход. Во-первых, количество пар может быть настолько велико, что не позволит хранить их все в памяти в используемом на практике приложении. Во-вторых, что гораздо важнее, не существует никакого простого метода, который сам по себе позволяет определить, связаны ли два объекта в наборе всех соединений, даже если бы удалось их все сохранить! Базовый метод, использующий этот подход, рассматривается в "Рекурсия и деревья" , а методы, которые рассматриваются в этой лекции, проще, поскольку они решают менее сложную задачу, и эффективнее, поскольку не требуют хранения всех пар. Для хранения информации, необходимой для реализации операций объединение и поиск, все эти методы используют массив целых чисел, каждое из которых соответствует отдельному объекту.
Массивы — это элементарные структуры данных, которые подробно будут рассмотрены в
"Элементарные структуры данных"
. Здесь же они используются в простейшей форме: мы объявляем, что собираемся использовать, скажем, 1000 целых чисел, записывая a[1000], а затем обращаемся к i-ому целому числу в массиве с помощью записи a[i] для 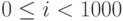 .
.
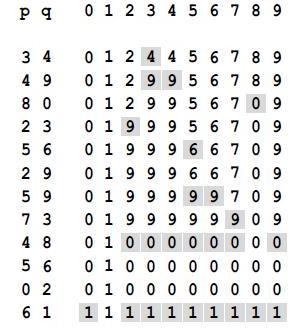
Программа 1.1 — реализация простого алгоритма, называемого алгоритмом быстрого поиска, который решает задачу связности. В основе этого алгоритма лежит использование массива целых чисел, обладающих тем свойством, что p и q связаны тогда и только тогда, когда p-й и q-й элементы массива равны. Вначале i-й элемент массива инициализируется значением i,  . Чтобы реализовать операцию объединение для p и q, мы просматриваем массив, заменяя все элементы с тем же именем, что и p, на элементы с тем же именем, что и q. Этот выбор произволен — можно было бы все элементы с тем же именем, что и q, заменять на элементы с тем же именем, что и p.
. Чтобы реализовать операцию объединение для p и q, мы просматриваем массив, заменяя все элементы с тем же именем, что и p, на элементы с тем же именем, что и q. Этот выбор произволен — можно было бы все элементы с тем же именем, что и q, заменять на элементы с тем же именем, что и p.
Изменения в массиве при выполнении операций объединение в примере из рис. 1.1 показаны на рис. 1.3. Для реализации операции поиск достаточно проверить указанные записи массива на предмет равенства — отсюда и название быстрый поиск (quick find). Однако операция объединение требует просмотра всего массива для каждой вводимой пары.
Лемма 1.1. Алгоритм быстрого поиска выполняет не менее M x N инструкций для решения задачи связности при наличии N объектов, для которых требуется выполнение M операций объединения.
Для каждой из M операций объединение цикл for выполняется N раз. Для каждой итерации требуется выполнение, по меньшей мере, одной инструкции (если только проверять, завершился ли цикл). 
Программа 1.1. Решение задачи связности методом быстрого поиска
Эта программа считывает из стандартного ввода последовательность пар неотрицательных целых чисел, меньших чем N (интерпретируя пару p q как указание "связать объект p с объектом q"), и выводит пары, соответствующие еще не связанным объектам. В ней используется массив id, содержащий элемент для каждого объекта и характеризующийся тем, что элементы id[p] и id[q] равны тогда и только тогда, когда объекты p и q связаны. Для простоты N определена как константа времени компиляции. Иначе можно было бы считывать ее из ввода и выделять массив id динамически (см. "Элементарные структуры данных" ).
#include <iostream.h>
static const int N = 10000;
int main() {
int i, p, q, id[N];
for ( i = 0; i < N; i++) id[i] = i;
while (cin >> p >> q) {
int t = id[p];
if (t == id[q]) continue;
for ( i = 0; i < N; i++)
if (id[i] == t) id[i] = id[q];
cout << " " << p << " " << q << endl;
}
}
Здесь изображено содержимое массива id после обработки каждой пары, приведенной слева, алгоритмом быстрого поиска (программа 1.1). Затененные записи — те, которые изменяются для выполнения операции объединение. При обработке пары p q во все записи со значением id[p] заносится значение из id[q].
Современные компьютеры могут выполнять десятки или сотни миллионов инструкций в секунду, поэтому для малых значений M и N эти затраты не заметны, но в современных приложениях может потребоваться обработка миллиардов объектов и миллионов вводимых пар. Поэтому мы неизбежно приходим к заключению, что подобную проблему нельзя решить приемлемым образом, используя алгоритм быстрого поиска (см. упражнение 1.10). Строгое обоснование этого заключения приведено в "Принципы анализа алгоритмов" .
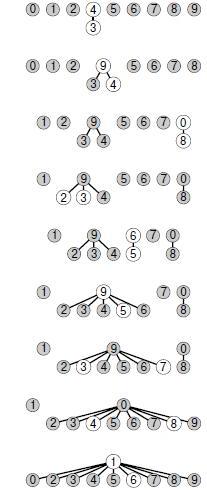
Графическое представление массива, показанного на рис. 1.3, приведено на рис. 1.4. Можно считать, что некоторые объекты представляют множество, к которому они принадлежат, а остальные указывают на представителя их множества. Причина обращения к такому графическому представлению массива вскоре станет понятна. Обратите внимание, что связи между объектами в этом представлении не обязательно соответствуют связям во вводимых парах — они представляют собой информацию, запоминаемую алгоритмом, которая позволяет определить, соединены ли пары, которые будут вводиться в будущем.
А теперь мы рассмотрим дополнительный к предыдущему метод, который называется алгоритмом быстрого объединения. В его основе лежит та же структура данных — индексированный по именам объектов массив — но в нем используется иная интерпретация значений, что приводит к более сложной абстрактной структуре. Каждый объект указывает на другой объект в этом же множестве, образуя структуру, не содержащую циклов. Чтобы определить, находятся ли два объекта в одном множестве, мы следуем указателям для каждого из них до тех пор, пока не будет достигнут объект, который указывает на самого себя. Объекты находятся в одном множестве тогда и только тогда, когда этот процесс приводит от них к одному и тому же объекту. Если они не находятся в одном множестве, процесс завершится на разных объектах (которые указывают на себя). Тогда для образования объединения достаточно связать один объект с другим — отсюда и название быстрое объединение (quick union).
На рис. 1.5 показано графическое представление, которое соответствует рис. 1.4 при выполнении алгоритма быстрого объединения для массива, изображенного на рис. 1.1, а на рис. 1.6 показаны соответствующие изменения в массиве id. Графическое представление структуры данных позволяет сравнительно легко понять действие алгоритма — пары объектов, которые соединены во входных данных, связаны один с другим и в структуре данных. Обратите внимание: здесь, как и ранее, связи в структуре данных не обязательно совпадают со связями, заданными вводимыми парами; вместо этого они создаются алгоритмом так, чтобы обеспечить эффективную реализацию операций объединение и поиск.
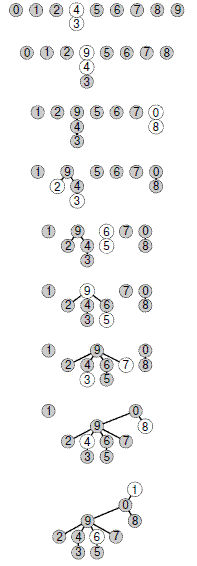
На этом рисунке показано графическое представление примера, приведенного на рис. 1.3. Связи на этом рисунке не обязательно представляют связи во входных данных. Например, структура, показанная на нижнем рисунке, содержит связь 1-7, которая отсутствует во входных данных, но образуется в результате цепочки связей 7-3-4-9-5-6-1.
Этот рисунок — графическое представление примера, показанного на рис. 1.3. Мы проводим линию от объекта i к объекту id[i].
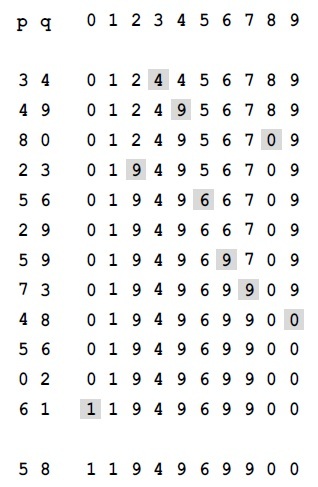
Здесь изображено содержимое массива id после обработки каждой из показанных слева пар алгоритмом быстрого поиска (программа 1.1). Затененные элементы — те, которые изменяются для выполнения операции объединения (по одной на каждую операцию). При обработке пары p q мы переходим по указателям из p до записи i, у которой id[i] == i; потом переходим по указателям из q до записи j, у которой id[j] == j; затем, если i и j различны, устанавливаем id[i] = id[j]. При выполнении операции поиска для пары 5-8 (последняя строка) i принимает значения 5 6 9 0 1, а j — значения 8 0 1.
Связанные компоненты, изображенные на рис. 1.5, называются деревьями (tree) — это основополагающие комбинаторные структуры, которые многократно встречаются в курсе. Свойства деревьев будут подробно рассмотрены в "Рекурсия и деревья" . Деревья, изображенные на рис. 1.5, удобны для выполнения операций объединение и поиск, поскольку их можно быстро построить, и они характеризуются тем, что два объекта связаны в дереве тогда и только тогда, когда объекты связаны во входных данных. Перемещаясь вверх по дереву, можно легко отыскать корень дерева, содержащего каждый объект, и, следовательно, можно выяснить, связаны они или нет. Каждое дерево содержит только один объект, указывающий сам на себя, называемый корнем (root) дерева. Указатель на себя на диаграммах не показан. Начав с любого объекта дерева и перемещаясь к объекту, на который он указывает, затем следующему указанному объекту и т.д., мы всегда со временем попадаем к корню. Справедливость этого свойства можно доказать методом индукции: это справедливо после инициализации массива, когда каждый объект указывает на себя, и если это справедливо до выполнения любой операции объединение, это безусловно справедливо и после нее.
Диаграммы для алгоритма быстрого поиска, показанные на рис. 1.4, характеризуются теми же свойствами, которые описаны в предыдущем абзаце. Различие состоит в том, что в деревьях быстрого поиска мы достигаем корня из всех узлов, переходя лишь по одной ссылке, а в дереве быстрого объединения для достижения корня может потребоваться переход по нескольким ссылкам.