НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 14: Классические и квантовые коды

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 611 / 26 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 10 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Код Шора [40].

Опишем серию кодов со сколь угодно большим кодовым расстоянием. Они используют 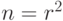n=r^2 кодовых q-битов и кодируют один q-бит (т.е. 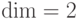$\dim\calM=2$ ), а кодовое расстояние равно .

Поскольку количество кодовых q-битов — точный квадрат, удобно задавать базисные состояния в таком кодовом пространстве в виде матрицы. В этих обозначениях код Шора порождается векторами

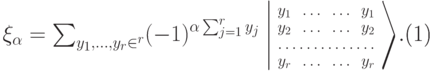$\begin{equation}\label{кодШора} \ket{\xi_\alpha}=\sum_{y_1,\dots, y_r\in\cb^r}^{} (-1)^{\alpha\sum_{j=1}^{r}y_j} \left.\Bigg| \hbox{\footnotesize\def\arraystretch{0.9} \begin{matrix} y_1&\dots&\dots&y_1\\ y_2&\dots&\dots&y_2\\ \hdotsfor{4}\\ y_r&\dots&\dots&y_r\\\end{matrix}}\right.\Bigg\rangle .\end{equation}$

( 14.11)

Для анализа кода Шора нам потребуется классификация операторов с помощью матриц Паули. Их, вообще говоря, три, но четвертой матрицей Паули будем считать единичную. Введем нестандартную индексацию матриц Паули:

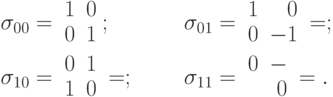
${\arraycolsep=0.5mm \tabcolsep=0.5mm $$\def\arraystretch{0.9} \begin{aligned} &\sigma_{00}= \hbox{$\leftp\begin{array}{*2 r} 1&0\\0&1 \end{array}\rightp$}; && \sigma_{01}= \hbox{$\leftp\begin{array}{*2 r} 1&0\\0&-1 \end{array}\rightp$}=\sz; \\ &\sigma_{10}= \hbox{$\leftp\begin{array}{*2 r} 0&1\\1&0 \end{array}\rightp$}=\sx;\qquad && \sigma_{11}= \hbox{$\leftp\begin{array}{*2 r} 0&-\ii\\ \ii&0 \end{array}\rightp$}=\sy. \end{aligned} $$ }$

Матрицы Паули замечательны тем, что они эрмитовы и унитарные одновременно. Введенная индексация позволяет удобно записывать коммутационные соотношения между матрицами Паули

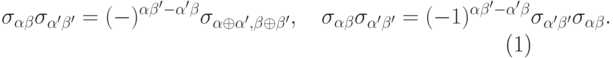$\begin{equation}\label{Паули-комм} \sigma_{\alpha\beta}\sigma_{\alpha'\beta'}= (-\ii)^{\alpha\beta'-\alpha'\beta} \sigma_{\alpha\oplus\alpha',\beta\oplus\beta'},\quad \sigma_{\alpha\beta}\sigma_{\alpha'\beta'}= (-1)^{\alpha\beta'-\alpha'\beta} \sigma_{\alpha'\beta'}\sigma_{\alpha\beta}. \end{equation}$

( 14.12)

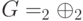Множество индексов образует группу $G=\ZZ_2\oplus\ZZ_2$ или 2-мерное пространство над полем $\FF_2$ .

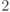Матрицы Паули образуют базис пространства $\LL(\BB)$ :

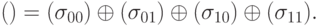
$\LL(\BB)=\CC(\sigma_{00})\oplus\CC(\sigma_{01})\oplus \CC(\sigma_{10})\oplus\CC(\sigma_{11}).$

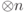Для пространства $\BB^{\otimes n}$ будет уже 4^n

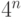базисных операторов. Введем обозначение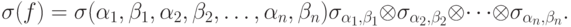

$\sigma(f)= \sigma(\alpha_1,\beta_1, \alpha_2,\beta_2, \dots, \alpha_n,\beta_n) \bydef \sigma_{\alpha_1,\beta_1}\otimes\sigma_{\alpha_2,\beta_2}\otimes \dots \otimes\sigma_{\alpha_n,\beta_n}.$

Здесь $f\in G^n=\FF_2^{\,2n}$ .

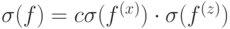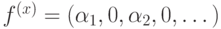Используя коммутационные соотношения, можно написать, с точностью до общего фазового множителя, $\sigma(f)=c\sigma(f^{(x)})\cdot\sigma(f^{(z)})$ , где $f^{(x)}=(\alpha_1,0,\alpha_2,0,\dots)$ называется классической ошибкой, а 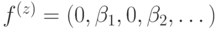$f^{(z)}\double=(0,\beta_1,0,\beta_2,\dots)$ — фазовой ошибкой.

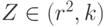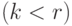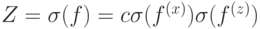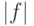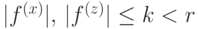Теперь проанализируем код Шора. В силу линейности определения достаточно ограничиться изучением базисных ошибок. Пусть $Z\double\in\calE(r^2,k)$ , (k<r) и $Z=\sigma(f)=c \sigma(f^{(x)})\sigma(f^{(z)})$ . Поскольку $|f|\leq k$ ( |f| — число ненулевых переменных в ), то $|f^{(x)}|,\, |f^{(z)}|\le k<r$ .

Достаточно показать, что в этом случае

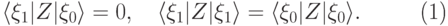$\begin{equation}\label {соотношения-ортогональности} \langle\xi_1|Z|\xi_0\rangle =0,\quad \langle\xi_1|Z|\xi_1\rangle=\langle\xi_0|Z|\xi_0\rangle. \end{equation}$

( 14.13)

Рассмотрим два случая.

Классическая ошибка отлична от 0. В этом случае каждое базисное состояние
$\left.\Bigg| \hbox{\footnotesize\def\arraystretch{0.9}\begin{matrix} y_1&\dots&\dots&y_1\\ y_2&\dots&\dots&y_2\\ \hdotsfor{4}\\ y_r&\dots&\dots&y_r\\ \end{matrix}}\right.\Bigg\rangle$
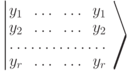
изменяется под действием в некоторых битах, 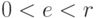. Поэтому в скалярных произведениях (14.13) все слагаемые будут равны 0.
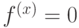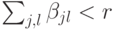$f^{(x)}=0$ . Ошибка чисто фазовая: $Z=\left(\sz\right)^{\beta_{11}}\otimes\dots\otimes \left(\sz\right)^{\beta_{rr}}$ , где $\sum_{j,l}\beta_{jl}<r$ . Обозначим 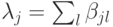$\lambda_j=\sum_{l}^{}\beta_{jl}$ . Тогда (см.(14.11))
$Z|\xi_\alpha\rangle\ =\ \sum_{y_1,\dots, y_r} (-1)^{\sum_j(\lambda_j+\alpha)y_j} \left.\Bigg| \hbox{\footnotesize\def\arraystretch{0.9} \begin {matrix} y_1&\dots&\dots&y_1\\ y_2&\dots&\dots&y_2\\ \hdotsfor{4}\\ y_r&\dots&\dots&y_r\\ \end{matrix}} \right\rangle\:.$
Нас интересуют значения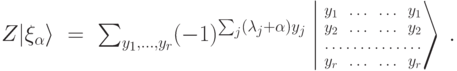 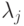по модулю 2. Возможны 3 случая:
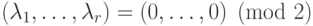1. $(\lambda_1,\dots,\lambda_r)=(0,\dots,0)\pmod 2$ .
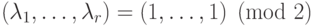2. $(\lambda_1,\dots,\lambda_r)=(1,\dots,1)\pmod 2$ .
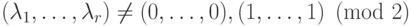3. $(\lambda_1,\dots,\lambda_r)\not=(0,\dots,0),(1,\dots,1)\pmod 2$ .
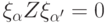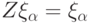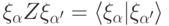Случай 2 в действительности реализоваться не может, так как $\sum_j\lambda_j\le k<r$ . В случае 3 все скалярные произведения обращаются в нуль, $\bra{\xi_\alpha}Z\ket{\xi_{\alpha'}}=0$ . В случае 1 $Z\ket{\xi_\alpha}=\ket{\xi_\alpha}$ , т.е. действует на кодовом подпространстве тождественным образом. (Такая ошибка, по существу, не является ошибкой, поскольку ничего не портит). Следовательно, $\bra{\xi_\alpha}Z\ket{\xi_{\alpha'}}= \langle\xi_\alpha|\xi_{\alpha'}\rangle$ .

Итак, код Шора обнаруживает r-1 ошибку; кодовое расстояние равно~ .

Замечание. Код Шора основан на дуальности между классическими и фазовыми ошибками, которая выражается равенством 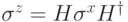$\sigma^z=H\sigma^x H^\dagger$ . Внутри каждой строки 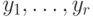$y_1,\dots,y_r$ реализован обычный повторительный код, исправляющий классические ошибки. Строки организованы в аналогичный код, отличающийся заменой базиса в каждом q-бите: 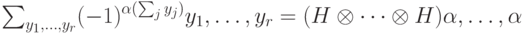$\sum_{y_1,\dots,y_r}(-1)^{\alpha(\sum_j y_j)}\ket{y_1,\dots,y_r}= (H\otimes\dots\otimes H)\ket{\alpha,\dots,\alpha}$ . Этот код исправляет фазовые ошибки.

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Классические и квантовые коды

Код Шора [40].

Вопросы и ответы