НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 12: Быстрые квантовые алгоритмы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 616 / 27 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Обсуждение алгоритма.

Обсудим два естественно возникающих вопроса по поводу изложенного алгоритма.

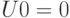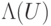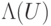— Можно ли находить собственные числа других операторов так же, как в алгоритме вычисления периода? Да, например, можно находить собственные числа таких операторов , для которых $U\ket0=\ket0$ , и есть полиномиальная схема реализации оператора $\Lambda(U)$ . (Из задачи 7.5 следует, что если для самого оператора есть полиномиальная схема, то и для оператора $\Lambda(U)$ ее также можно построить).

Точность определения собственных чисел произвольного оператора невелика, полиномиально зависит от размера схемы. Если можно эффективно вычислять степени оператора (как и было в рассмотренном алгоритме), то точность можно сделать экспоненциальной.

— Какие собственные числа мы находим?

Мы находим значение случайно выбранного собственного числа. Распределением по множеству всех собственных чисел можно управлять, выбирая начальное состояние (в алгоритме вычисления периода — 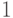$\ket1$ ). Если взять в качестве начального состояние, задаваемое диагональной матрицей плотности

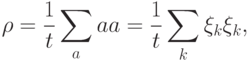
$\rho=\frac{1}{t}\sum\limits_{a}^{} \ket{a}\bra{a} =\frac{1}{t}\sum\limits_{k}^{} \ket{\xi_k}\bra{\xi_k},$

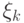где $\ket{\xi_k}$ пробегает множество собственных векторов

, то получим равномерное распределение на множестве всех собственных чисел. В алгоритме нахождения периода начальное состояние выбиралось иначе: мы выбирали такой вектор, чтобы получить равномерное распределение на собственных числах, соответствующих определенной орбите, остальные собственные числа не порождались.

Задача 12.3. Постройте квантовую схему размера 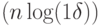$\poly(n\log(\slashfrac1\delta))$ , реализующую преобразование Фурье на группе 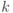$\ZZ_k$ при любом 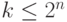$k\le 2^n$ с точностью $\delta$ . (Определение см. в задаче 8.4. Указание: воспользуйтесь результатом задачи 11.2).

Задача о скрытой подгруппе в 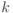$\ZZ^k$ .

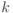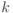Алгоритмы, открытые Саймоном и Шором, обобщаются на довольно широкий класс задач, связанных с абелевыми группами. Самой общей из них является задача о скрытой подгруппе в $\ZZ^k$ [23]. К ней сводится задача о скрытой подгруппе в любой конечно-порожденной абелевой группе , поскольку можно представить как фактор-группу $\ZZ^k$ (для некоторого ).

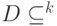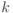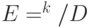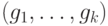"Скрытая подгруппа" $D\subseteq\ZZ^k$ изоморфна $\ZZ^k$ , поскольку она имеет конечный индекс: порядок группы $E=\ZZ^k/D$ не превосходит 2^n . С вычислительной точки зрения представляется базисом $(g_1,\dots,g_k)$ , двоичная запись которого имеет длину 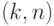$\poly(k,n)$ . Любой такой базис считается решением задачи. (Эквивалентность двух базисов можно проверить при помощи полиномиального алгоритма).

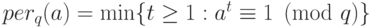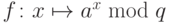Задача о вычислении периода является частным случаем задачи о скрытой подгруппе в $\ZZ$ . Напомним, что $per_q(a)=\min\{t\geq1: a^t\equiv1\pmod q\}$ . Фунция $f\colon x\mapsto a^x\bmod q$ удовлетворяет условию (12.1), где 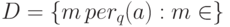$D=\{m\,per_q(a): m\in\ZZ\}$ . Эта функция полиномиально вычислима, поэтому любой полиномиальный алгоритм нахождения скрытой подгруппы преобразуется в полиномиальный алгоритм решения задачи о вычислении периода.

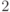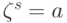Известная задача вычисления дискретного логарифма может быть сведена к задаче о скрытой подгруппе в $\ZZ^2$ . Дискретным логарифмом числа по основанию $\zeta$ , где $\zeta$ — некоторый первообразный корень по модулю простого числа (образующая $(\ZZ/q\ZZ)^*$ ), называется наименьшее положительное число такое, что $\zeta^s=a$ . Рассмотрим функцию 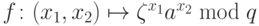$f\colon (x_1,x_2)\mapsto\zeta^{x_1}a^{x_2}\bmod q$ . Эта функция также удовлетворяет условию (12.1), где 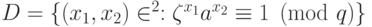$D=\{(x_1,x_2)\in\ZZ^2: \zeta^{x_1} a^{x_2}\equiv 1\pmod q\}$ . Зная базис подгруппы 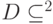$D\subseteq\ZZ^2$ , легко найти элемент вида 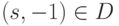$(s,-1)\in D$ . Тогда 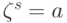$\zeta^s=a$ , т.е. есть дискретный логарифм по основанию $\zeta$ .

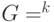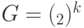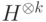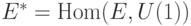Опишем квантовый алгоритм решения задачи о скрытой подгруппе в $G=\ZZ^k$ . Он аналогичен алгоритму для случая $G=(\ZZ_2)^k$ , только вместо оператора $H^{\otimes k}$ используется процедура измерения собственных чисел. Вместо базиса самой группы мы будем искать систему образующих для группы характеров $E^*=\mathop{\rm Hom}(E, U(1))$ (переход от E^* к осуществляется при помощи полиномиального алгоритма, см., например,[14, Т.1]). Характер

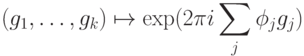
$(g_1,\dots,g_k)\mapsto\exp(2\pi i\sum_j\phi_jg_j)$

задается набором чисел $\phi_1,\dots,\phi_k$ по модулю

. Это рациональные числа со знаменателями не больше $|E^*|\le 2^n$ .

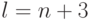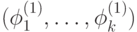
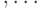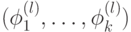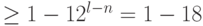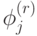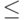Если породить l=n+3 случайных равномерно распределенных характера $(\phi_1^{(1)},\dots,\phi_k^{(1)})$ $,\dots$ , $(\phi_1^{(l)},\dots,\phi_k^{(l)})$ , то они порождают всю группу E^* с вероятностью $\ge 1-\slashfrac{1}{2^{l-n}}=1-\slashfrac{1}{8}$ (см. задачу 12.1). Каждую из величин $\phi_j^{(r)}$ достаточно знать с точностью $\delta$ и вероятностью ошибки $\le\eps$ , где

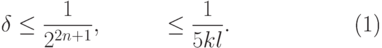$\begin{equation}\label{deltaeps} \delta\le\frac{1}{2^{2n+1}},\qquad\quad \eps\le\frac{1}{5kl}. \end{equation}$

( 12.3)

Последнее условие гарантирует, что суммарная вероятность ошибки будет не больше, чем $\slashfrac{1}{8}+\slashfrac{1}{5}<\slashfrac{1}{3}$ .

Выберем достаточно большое число M=2^m (конкретная оценка получается из анализа алгоритма). Мы будем работать с целыми числами в диапазоне от до M-1 .

Приготовим в одном квантовом регистре длины состояние

$\ket{\xi}=M^{-k/2}\sum_{g\in\Delta} \ket{g},\ \text{где}\ \Delta=\{0,\dots,M-1\}^k.$

В другой регистр поместим $\ket{0^n}$ . Применим квантовый оракул (12.2) и выбросим второй регистр. Получится смешанное состояние

$\rho=\Tr_{[km+1,\dots,km+n]}\Bigl(U\bigl(\ket{\xi}\bra{\xi}\otimes\ket{0^n}\bra{0^n} \bigr)U^\dagger \Bigr)= M^{-k}\mkern-6mu \sum_{g,h\in\Delta:g-h\in D}\mkern-3mu \ket{g}\bra{h}.$

Теперь мы собираемся измерить собственные значения операторов сдвига по модулю :

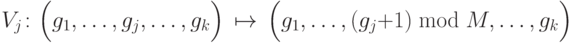
$V_j\colon \Bigl(g_1,\dots,g_j,\dots,g_k\Bigr) \,\mapsto\, \Bigl(g_1,\dots,(g_j+1)\bmod M,\dots,g_k\Bigr)$

(меняется только

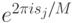-ая компонента). Эти операторы коммутируют, поэтому у них есть общий базис из собственных векторов, и, значит, можно определять их собственные числа одновременно. Собственные числа имеют вид $e^{2\pi is_j/M}$ . Соответствующие собственные векторы равны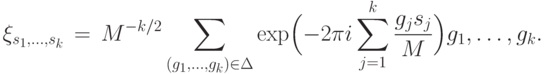

$\ket{\xi_{s_1,\dots,s_k}} \,=\, M^{-k/2} \sum_{(g_1,\dots,g_k)\in\Delta} \exp\Bigl(-2\pi i\sum_{j=1}^{k}\frac{g_js_j}{M}\Bigr) \ket{g_1,\dots,g_k}.$

Вероятность того, что реализуется данный набор 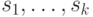$s_1,\dots,s_k$ , равна

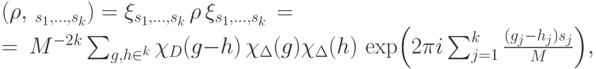
$\begin{equation*} &\PP(\rho,\,\calL_{s_1,\dots,s_k}) = \bra{\xi_{s_1,\dots,s_k}}\,\rho\,\ket{\xi_{s_1,\dots,s_k}}\, =\\ =&\ M^{-2k} \sum_{g,h\in\ZZ^k}\chi_D(g-h)\,\chi_\Delta(g)\chi_\Delta(h)\, \exp\Bigl(2\pi i\sum_{j=1}^{k}\frac{(g_j-h_j)s_j}{M}\Bigr), \end{equation*}$

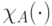где $\chi_A(\cdot)$ обозначает характеристическую функцию множества

. Фурьеобраз от произведения равен свертке фурье-образов сомножителей. Таким образом, получаем:

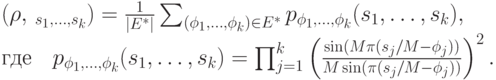
$\begin{equation*} &\PP(\rho,\,\calL_{s_1,\dots,s_k}) = \frac{1}{|E^*|} \sum_{(\phi_1,\dots,\phi_k)\in E^*} p_{\phi_1,\dots,\phi_k}(s_1,\dots,s_k),\\ \text{где}\quad& p_{\phi_1,\dots,\phi_k}(s_1,\dots,s_k) = \prod_{j=1}^{k} \left(\frac{\sin(M\pi(s_j/M-\phi_j))}{M\sin(\pi(s_j/M-\phi_j))}\right)^2. \end{equation*}$

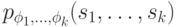При заданных значениях $\phi_1,\dots,\phi_k$ функция $p_{\phi_1,\dots,\phi_k}(s_1,\dots,s_k)$ является вероятностным распределением, относительно которого

$\Pr\Bigl[|s_j/M-\phi_j|>\beta\Bigr] \,\le\, \frac{1}{M\beta}$

( $\beta$ — любое). Мы измеряем величины s_j/M

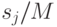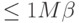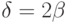(как уже говорилось, измерение одной из них не меняет значения другой); при этом нас устроит точность $\beta$ и вероятность ошибки $\le\slashfrac{1}{M\beta}$ . Тем самым мы получаем значения $\phi_1,\dots,\phi_k$ с точностью $\delta=2\beta$ и вероятностью ошибки 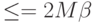$\le\eps=\slashfrac{2}{M\beta}$ . Теперь осталось подобрать числа

и $\beta$ , чтобы удовлетворить неравенствам 12.3.

Сложность алгоритма.

Tребуется O(n) обращений к оракулу, каждый вопрос имеет длину $O(k(n+\log k))$ . Размер квантовой схемы оценивается как $O(kn^3)\poly(\log k,\log n)$ .

Замечание. Для измерения собственных чисел операторов 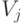V_j можно воспользоваться квантовым преобразованием Фурье на группе 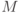$\ZZ_M$ при M=2^m (см. задачу 8.4). Это позволяет несколько уменьшить размер схемы (на логарифмический множитель), однако приходится использовать нестандартные элементы.

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Быстрые квантовые алгоритмы

Обсуждение алгоритма.

Сложность алгоритма.

Вопросы и ответы