НОУ ИНТУИТ | Классические и квантовые вычисления. Лекция 12: Быстрые квантовые алгоритмы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Московский государственный университет имени М.В.Ломоносова

Опубликован: 15.03.2007 | Доступ: свободный | Студентов: 613 / 26 | Оценка: 5.00 / 4.50 | Длительность: 19:30:00

Тема: Алгоритмы и дискретные структуры

Специальности: Программист

|

Вам нравится? Нравится 10 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Экспоненциально точное определение собственных чисел.

Для увеличения точности мы будем использовать, наряду с 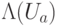$\Lambda(U_a)$ , операторы 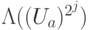$\Lambda((U_a)^{2^j})$ для всех 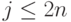$j\le 2n$ . Числа мы можем быстро возводить в степень, а операторы, вообще говоря, — нет. Но оператор умножения на число U_a обладает следующим замечательным свойством:

$(U_a)^p = U_{a^p\bmod q}.$

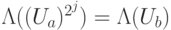Следовательно, $\Lambda((U_a)^{2^j})=\Lambda(U_b)$ , где $b\equiv a^{2^j}\pmod q$ . Нужные нам значения параметра

можно вычислить при помощи схемы полиномиального размера, а затем использовать результат задачи 12.2.

Вход: и

Вычисление степеней 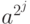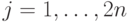$a^{2^j}$ ( $j=1,\dots,2n$ ) по модулю (классическое).
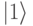Cоздание штук квантовых регистров, содержащих базисное состояние $|1\rangle$ .

увеличить изображение
Вычисление наибольшего общего знаменателя (классическое).

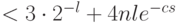Ответ: (с вероятностью ошибки $<3\cdot 2^{-l}+4nle^{-cs}$ , где $c={\rm const}$ )

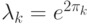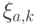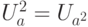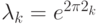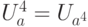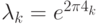Вернемся к схеме упоминаемой ранее. Мы находили собственное число $\lambda_k=e^{2\pi\ii\ph_k}$ для некоторого собственного вектора $\ket{\xi_{a,k}}$ . Этот же вектор останется собственным и для любой степени оператора U_a , поэтому можно на одном и том же квантовом регистре искать собственное число для $U_a^2=U_{a^2}$ , оно равно $\lambda_k=e^{2\pi\ii2\ph_k}$ ; для $U_a^4=U_{a^4}$ оно равно $\lambda_k\double=e^{2\pi\ii4\ph_k}$ ;...

Другими словами, мы можем с точностью 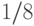1/8 определить значения 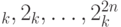$\ph_k, 2\ph_k, \dots, 2^{2n}\ph_k$ по модулю 1. Но это позволяет определить 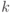$\ph_k$ с точностью $1/2^{2n+1}$ за полиномиальное время .

Идея доказательства. Множество возможных значений 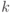$\ph_k$ удобно представлять в виде окружности единичной длины. Зная 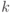$\ph_k$ с точностью 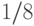1/8 , мы выделяем дугу в 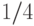1/4 от всей окружности. Знание 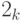$2\ph_k$ с точностью 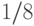1/8 позволяет выделить две дуги длиной 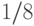1/8 каждая, причем только одна из них имеет непустое пересечение с предыдущей дугой.

Важные замечания.

Существенно, что вектор 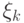$\ket{\xi_k}$ не портится во время вычислений.
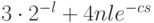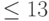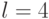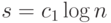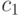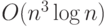Все вычисление в целом зависит от параметров и . Cуммарная вероятность ошибки не превышает $3\cdot 2^{-l}+4nle^{-cs}$ , где $c={\rm const}$ . Если требуется получить ответ с вероятностью ошибки $\le\slashfrac{1}{3}$ , следует положить , $s=c_1\log n$ , где — некоторая константа. При этом получается квантовая схема размера $O(n^3\log n)$ .

Дальше >>

Авторизоваться

Классические и квантовые вычисления

Быстрые квантовые алгоритмы

Экспоненциально точное определение собственных чисел.

Важные замечания.

Вопросы и ответы