Быстрые квантовые алгоритмы
Квантовый алгоритм нахождения периода: основная идея.
Рассмотрим оператор умножения вычета на  , действующий по правилу
, действующий по правилу 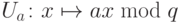 . (Более корректное обозначение —
. (Более корректное обозначение — 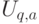 , однако число
, однако число  не меняется на протяжении всего вычисления, поэтому мы опускаем его в индексах). Этот оператор переставляет базисные векторы при
не меняется на протяжении всего вычисления, поэтому мы опускаем его в индексах). Этот оператор переставляет базисные векторы при 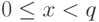 (напомним, что
(напомним, что  ). Будем считать, что на остальных базисных векторах он действует тождественно,
). Будем считать, что на остальных базисных векторах он действует тождественно, 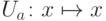 при
при  .
.
Поскольку для умножения вычетов есть обычная булева схема полиномиального — 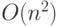 — размера, то существует и квантовая схема примерно такого же размера (использующая напрокат дополнительные q-биты, как это объяснялось раньше).
— размера, то существует и квантовая схема примерно такого же размера (использующая напрокат дополнительные q-биты, как это объяснялось раньше).
Перестановка, которую задает оператор  , разбивается на циклы. Цикл, содержащий
, разбивается на циклы. Цикл, содержащий  , содержит и
, содержит и  (после
(после 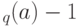 итераций мы попадаем из
итераций мы попадаем из  в
в  ). Алгоритм, о котором пойдет речь, начинает с состояния
). Алгоритм, о котором пойдет речь, начинает с состояния 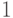 и применяет к нему оператор
и применяет к нему оператор  по многу раз. Но за пределы орбиты
по многу раз. Но за пределы орбиты  (цикла перестановки, которому принадлежит
(цикла перестановки, которому принадлежит  ) мы такими преобразованиями не выйдем. Поэтому рассмотрим ограничение оператора
) мы такими преобразованиями не выйдем. Поэтому рассмотрим ограничение оператора  на подпространство, порожденное орбитой
на подпространство, порожденное орбитой  .
.
Собственные числа для 
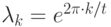 , где
, где  — период.
— период.
Легко проверить, что написанные векторы действительно собственные. Достаточно заметить, что умножение на  приводит к сдвигу индексов в сумме. Если заменить переменную суммирования, чтобы устранить этот сдвиг, получим множитель
приводит к сдвигу индексов в сумме. Если заменить переменную суммирования, чтобы устранить этот сдвиг, получим множитель 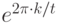 .
.
Если бы мы могли измерять собственные числа оператора  , то получали бы числа
, то получали бы числа  . Сначала разберем, как это может нам помочь в нахождении периода.
. Сначала разберем, как это может нам помочь в нахождении периода.
Пусть у нас есть машина  , которая при каждом запуске выдает нам число
, которая при каждом запуске выдает нам число  , где
, где  — искомый период, а
— искомый период, а  — равномерно распределенное на множестве
— равномерно распределенное на множестве 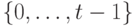 случайное число. Мы предполагаем, что
случайное число. Мы предполагаем, что  представлено в виде несократимой дроби
представлено в виде несократимой дроби  (если бы машина выдавала число в виде
(если бы машина выдавала число в виде  , то вообще не было бы проблем).
, то вообще не было бы проблем).
Получив несколько дробей такого вида 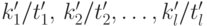 , можно с большой вероятностью найти число
, можно с большой вероятностью найти число  , приводя эти дроби к общему знаменателю.
, приводя эти дроби к общему знаменателю.
Лемма. Если получено  дробей, то вероятность того, что наименьшее общее кратное их знаменателей отлично от
дробей, то вероятность того, что наименьшее общее кратное их знаменателей отлично от  , меньше
, меньше  .
.
Доказательство. Дроби 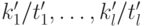 получаются сокращением дробей
получаются сокращением дробей 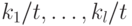 (т.е.
(т.е. 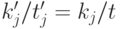 ), где
), где 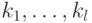 — независимо распределенные случайные числа. Достаточно, чтобы эти числа были в совокупности взаимно просты, тогда наименьшее общее кратное
— независимо распределенные случайные числа. Достаточно, чтобы эти числа были в совокупности взаимно просты, тогда наименьшее общее кратное 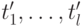 будет равно
будет равно  .
.
Вероятность того, что 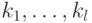 имеют общий простой делитель
имеют общий простой делитель  , не больше, чем
, не больше, чем 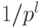 . Поэтому вероятность получить не
. Поэтому вероятность получить не  после приведения к общему знаменателю не превосходит
после приведения к общему знаменателю не превосходит 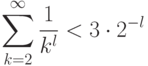 (эта сумма заведомо включает в себя все простые, меньшие
(эта сумма заведомо включает в себя все простые, меньшие  ).
).
Теперь будем строить машину  . Она должна содержать схему, измеряющую собственные числа оператора
. Она должна содержать схему, измеряющую собственные числа оператора 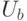 для любого
для любого  (а не только для
(а не только для  — числа, для которого ищется период). Точнее говоря, нам нужен оператор
— числа, для которого ищется период). Точнее говоря, нам нужен оператор 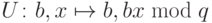 , если
, если 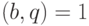 . Как оператор
. Как оператор  действует в остальных случаях, неважно. Его можно доопределить любым вычислительно тривиальным способом. На самом деле, все приведенные ранее рассуждения об имитации классических схем квантовыми сохраняют силу и для имитации схем, вычисляющих частично определенные функции.
действует в остальных случаях, неважно. Его можно доопределить любым вычислительно тривиальным способом. На самом деле, все приведенные ранее рассуждения об имитации классических схем квантовыми сохраняют силу и для имитации схем, вычисляющих частично определенные функции.
Задача 12.2. Используя оператор  , реализуйте оператор
, реализуйте оператор 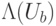 для любого
для любого  , взаимно простого с
, взаимно простого с  .
.
Обозначим 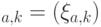 (подпространство, порожденное
(подпространство, порожденное 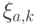 ), тогда искомая схема должна реализовывать измеряющий оператор
), тогда искомая схема должна реализовывать измеряющий оператор 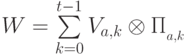 с операторами
с операторами  вида
вида 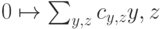 , где
, где  — некоторая несократимая дробь, а
— некоторая несократимая дробь, а  — мусор. При этом для условных вероятностей должно выполняться неравенство
— мусор. При этом для условных вероятностей должно выполняться неравенство
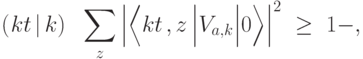
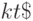 , обозначает несократимую дробь, представляющую рациональное число
, обозначает несократимую дробь, представляющую рациональное число 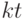 .
.Построение такой измеряющей схемы довольно сложное, поэтому вначале объясним, как из нее строится машина  . Возьмем состояние
. Возьмем состояние 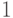 в качестве начального. Прямое вычисление (читателю рекомендуется его проделать) показывает, что
в качестве начального. Прямое вычисление (читателю рекомендуется его проделать) показывает, что
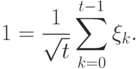
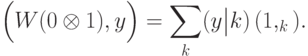
Вероятности всех 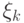 равны:
равны: 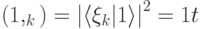 , а указанное выше свойство условных вероятностей гарантирует нам, что с вероятностью
, а указанное выше свойство условных вероятностей гарантирует нам, что с вероятностью  будет получаться
будет получаться 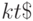 ,. Как будет видно в дальнейшем, при построении
,. Как будет видно в дальнейшем, при построении  можно сделать величину
можно сделать величину 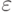 сколь угодно малой.
сколь угодно малой.
Условно работу машины  можно представить в виде такого процесса:
можно представить в виде такого процесса:
(Cлучайный выбор  происходит сам по себе, без применения какого бы то ни было оператора. Просто формула полной вероятности устроена так, как будто до начала измерения генерируется случайное
происходит сам по себе, без применения какого бы то ни было оператора. Просто формула полной вероятности устроена так, как будто до начала измерения генерируется случайное  , которое затем остается постоянным. Разумеется, формула условной вероятности верна только тогда, когда оператор
, которое затем остается постоянным. Разумеется, формула условной вероятности верна только тогда, когда оператор  является измеряющим для заданных подпространств
является измеряющим для заданных подпространств 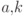 ).
).

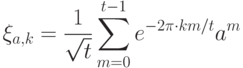 .
.