Функции
Иногда вместо функций говорят об отображениях (резервируя термин " функция" для отображений с числовыми аргументами и значениями). Мы не будем строго придерживаться таких различий, употребляя слова " отображение" и " функция" как синонимы.
Функция 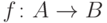 называется инъективной, или инъекцией, или вложением,
если она переводит
разные элементы в разные, то есть если
называется инъективной, или инъекцией, или вложением,
если она переводит
разные элементы в разные, то есть если  при различных
при различных  и
и  .
.
Функция 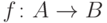 называется сюръективной, или сюръекцией, или наложением,
если множество ее значений есть
все
называется сюръективной, или сюръекцией, или наложением,
если множество ее значений есть
все  . (Иногда такие функции называют отображениями
на
. (Иногда такие функции называют отображениями
на  .)
.)
Эти два определения более симметричны, чем может показаться на первый взгляд, как показывают такие задачи:
61. Докажите, что функция 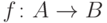 является вложением
тогда и только тогда, когда она имеет левую обратную
функцию
является вложением
тогда и только тогда, когда она имеет левую обратную
функцию 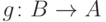 , то есть функцию
, то есть функцию  ,
для которой
,
для которой  .
Докажите, что функция
.
Докажите, что функция 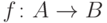 является наложением
тогда и только тогда, когда она имеет правую обратную
функцию
является наложением
тогда и только тогда, когда она имеет правую обратную
функцию 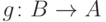 , для которой
, для которой 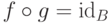 .
.
62. Докажите, что функция 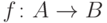 является вложением тогда и
только тогда, когда на нее можно сокращать слева: из равенства
является вложением тогда и
только тогда, когда на нее можно сокращать слева: из равенства  следует равенство
следует равенство  (для
любых функций
(для
любых функций 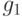 ,
,  , области значений которых
содержатся в
, области значений которых
содержатся в  ).
Докажите, что функция
).
Докажите, что функция 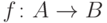 является наложением тогда
и
только тогда, когда на нее можно сокращать справа: из равенства
является наложением тогда
и
только тогда, когда на нее можно сокращать справа: из равенства  следует равенство
следует равенство  (для
любых функций
(для
любых функций 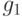 ,
,  , область определения которых
есть
, область определения которых
есть  ).
).
Отображение (функция) 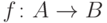 , которое одновременно
является инъекцией и сюръекцией (вложением и наложением),
называется биекцией, или взаимно однозначным
соответствием.
, которое одновременно
является инъекцией и сюръекцией (вложением и наложением),
называется биекцией, или взаимно однозначным
соответствием.
Если  - биекция, то существует обратная функция
- биекция, то существует обратная функция 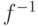 , для которой
, для которой  .
.
63. Могут ли для некоторой функции левая и правая обратные существовать, но быть различны?
Напомним, что множества  и
и  равномощны, если существует
биекция
равномощны, если существует
биекция 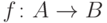 . В каком случае существует инъекция
(вложение)
. В каком случае существует инъекция
(вложение) 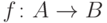 ? Легко понять, что вложение является
взаимно однозначным соответствием между
? Легко понять, что вложение является
взаимно однозначным соответствием между  и некоторым
подмножеством множества
и некоторым
подмножеством множества  , поэтому такое
вложение существует тогда и
только тогда, когда в
, поэтому такое
вложение существует тогда и
только тогда, когда в  есть подмножество,
равномощное
есть подмножество,
равномощное  , - когда мощность
, - когда мощность  не превосходит
мощности
не превосходит
мощности  (в смысле определения, данного в
"лекцию 3"
).
(в смысле определения, данного в
"лекцию 3"
).
Чуть менее очевиден другой результат: наложение  на
на  существует тогда и только тогда, когда мощность
существует тогда и только тогда, когда мощность  не
превосходит мощности
не
превосходит мощности  .
.
В самом деле, пусть наложение 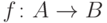 существует. Для
каждого элемента
существует. Для
каждого элемента 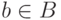 найдется хотя бы один
элемент
найдется хотя бы один
элемент 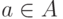 ,
для которого
,
для которого 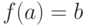 . Выбрав по одному такому элементу, мы
получим подмножество
. Выбрав по одному такому элементу, мы
получим подмножество 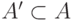 , которое находится во
взаимно однозначном соответствии с множеством
, которое находится во
взаимно однозначном соответствии с множеством  . (Здесь
снова используется аксиома выбора,
о которой мы говорили
ранее)
. (Здесь
снова используется аксиома выбора,
о которой мы говорили
ранее)
В обратную сторону: если какое- то подмножество 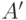 множества
множества  равномощно множеству
равномощно множеству  и имеется биекция
и имеется биекция 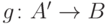 ,
то наложение
,
то наложение  на
на  можно получить, доопределив эту
биекцию на
элементах вне
можно получить, доопределив эту
биекцию на
элементах вне 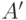 каким угодно образом.
каким угодно образом.
64. Найдите ошибку в этом рассуждении, не читая дальше.
На самом деле такое продолжение возможно, только если  непусто,
так что правильное утверждение звучит так:
наложение
непусто,
так что правильное утверждение звучит так:
наложение  на
на  существует тогда и только тогда, когда
существует тогда и только тогда, когда  непусто и
равномощно некоторому подмножеству
непусто и
равномощно некоторому подмножеству  , или когда
оба множества пусты.
, или когда
оба множества пусты.
В нашем изложении остается еще один не вполне понятный момент:
что такое " упорядоченная пара "?
Неформально говоря, это
способ из двух объектов  и
и  образовать один
объект
образовать один
объект 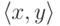 , причем этот способ обладает таким
свойством:
, причем этот способ обладает таким
свойством:

 обозначает множество,
единственным элементом которого является
обозначает множество,
единственным элементом которого является  , а
, а 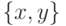 обозначает
множество, которое содержит
обозначает
множество, которое содержит  и
и  и не содержит
других элементов.
Тем самым
и не содержит
других элементов.
Тем самым 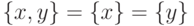 , если
, если 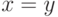 .)
.)Теорема 9. Упорядоченная пара по Куратовскому. Определим 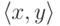 как
как 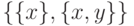 .
Тогда выполнено указанное выше свойство:
.
Тогда выполнено указанное выше свойство:

Доказательство. Пусть  .
По определению это означает, что
.
По определению это означает, что
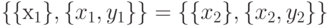
 с
с  ). Это удобно делать в следующем порядке. Пусть сначала
). Это удобно делать в следующем порядке. Пусть сначала 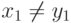 . Тогда множество
. Тогда множество  состоит из
двух элементов. Раз оно принадлежит левой части равенства, то
принадлежит и правой. Значит, оно равно либо
состоит из
двух элементов. Раз оно принадлежит левой части равенства, то
принадлежит и правой. Значит, оно равно либо 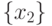 , либо
, либо 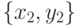 . Первое невозможно, так как двухэлементное
множество не может быть равно одноэлементному. Значит,
. Первое невозможно, так как двухэлементное
множество не может быть равно одноэлементному. Значит,  . С другой стороны,
одноэлементное множество
. С другой стороны,
одноэлементное множество 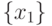 принадлежит левой части
равенства, поэтому оно принадлежит и правой, и потому равно
принадлежит левой части
равенства, поэтому оно принадлежит и правой, и потому равно 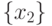 (поскольку не может быть равно двухэлементному).
Отсюда
(поскольку не может быть равно двухэлементному).
Отсюда  и
и  , что и
требовалось.
, что и
требовалось.Аналогично можно разобрать симметричный случай, когда 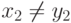 .
.
Осталось рассмотреть ситуацию, когда 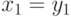 и
и 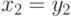 . В этом случае
. В этом случае 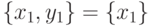 и
потому
левая часть данного нам равенства есть
и
потому
левая часть данного нам равенства есть 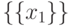 .
Аналогичным образом, правая его часть есть
.
Аналогичным образом, правая его часть есть 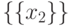 , и
потому
, и
потому  , так что все четыре элемента
, так что все четыре элемента  ,
,  ,
, 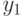 ,
, 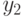 совпадают.
совпадают.
Заметим, что возможны и другие определения упорядоченной пары, для которых аналогичное утверждение верно, так что никакого " философского смысла" в этом определении нет - это просто удобный технический прием.
65. Докажите утверждение теоремы 9 для упорядоченной пары по Винеру: 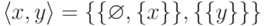 .
.
