Счетные множества

Теорема 3. Если множество бесконечно, а множество конечно или счетно, то объединение 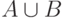равномощно .

Доказательство

Можно считать, что не пересекается с (пересечение можно выбросить из , останется по-прежнему конечное или счетное множество).

Выделим в счетное подмножество ; остаток обозначим через . Тогда нам надо доказать, что 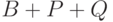равномощно (знак 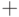символизирует объединение непересекающихся множеств). Поскольку и оба счетны, между ними существует взаимно однозначное соответствие. Его легко продолжить до соответствия между 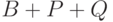и (каждый элемент множества соответствует сам себе).

35. Примените эту конструкцию и явно укажите соответствие между отрезком и полуинтервалом .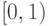

36. Теорема 3 показывает, что добавление счетного множества к бесконечному не меняет его мощности. Можно ли сказать то же самое про удаление? Докажите, что если бесконечно и не является счетным, а конечно или счетно, то равномощно .

37. Немецкий математик Р.Дедекинд предложил такое определение бесконечного множества: множество бесконечно, если оно равномощно некоторому своему подмножеству, не совпадающему со всем множеством. Покажите, что указанное Дедекиндом свойство действительно определяет бесконечные множества.

Добавляя конечные или счетные множества, легко понять, что прямая, все промежутки на прямой (отрезки, интервалы, полуинтервалы), лучи, их конечные или счетные объединения и т.п. равномощны друг другу.

38. Укажите взаимно однозначное соответствие между множеством и отрезком .

39. Докажите, что множество всех прямых на плоскости равномощно множеству всех точек на плоскости. (Указание: и точки, и прямые задаются парами чисел - за небольшими исключениями.)

40. Докажите, что полуплоскость (точки плоскости, лежащие по одну сторону от некоторой прямой) равномощна плоскости. (Это верно независимо от того, включаем мы граничную прямую в полуплоскость или нет.)

Теорема 4. Отрезок равномощен множеству всех бесконечных последовательностей нулей и единиц.

Доказательство. В самом деле, каждое число записывается в виде бесконечной двоичной дроби. Первый знак этой дроби равен или в зависимости от того, попадает ли число в левую или правую половину отрезка. Чтобы определить следующий знак, надо выбранную половину поделить снова пополам и посмотреть, куда попадет , и т.д.

Это же соответствие можно описать в другую сторону: последовательности 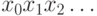соответствует число, являющееся суммой ряда

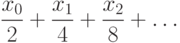
Описанное соответствие пока что не совсем взаимно однозначно: двоично-рациональные числа (дроби вида 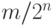) имеют два представления. Например, число 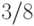можно записать как в виде , так и в виде 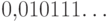Соответствие станет взаимно однозначным, если отбросить дроби с единицей в периоде (кроме дроби 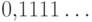, которую надо оставить). Но таких дробей счетное число, поэтому на мощность это не повлияет.

Какая двоичная дробь соответствует числу ?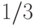

В этом доказательстве можно было бы использовать более привычные десятичные дроби вместо двоичных. Получилось бы, что отрезок равномощен множеству всех бесконечных последовательностей цифр 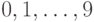. Чтобы перейти отсюда к последовательностям нулей и единиц, можно воспользоваться приемом, описанным ранее.

Теперь все готово для доказательства такого удивительного факта:

Теорема 5. Квадрат (со внутренностью) равномощен отрезку.

Доказательство. Квадрат равномощен множеству пар действительных чисел, каждое из которых лежит на отрезке (метод координат). Мы уже знаем, что вместо чисел на отрезке можно говорить о последовательностях нулей и единиц. Осталось заметить, что паре последовательностей нулей и единиц 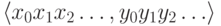можно поставить в соответствие последовательность-смесь 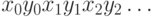и что это соответствие будет взаимно однозначным.

Этот результат был получен в 1877 году немецким математиком Георгом Кантором и удивил его самого, поскольку противоречил интуитивному ощущению " размерности" (квадрат двумерен, поэтому вроде бы должен содержать больше точек, чем одномерный отрезок). Вот что Кантор писал Дедекинду (20 июня 1877 года), обсуждая вопрос о равномощности пространств разного числа измерений: " Как мне кажется, на этот вопрос следует ответить утвердительно, хотя на протяжении ряда лет я придерживался противоположного мнения".

В одном из ответных писем Дедекинд отмечает, что результат Кантора не лишает смысла понятие размерности, поскольку можно рассматривать лишь непрерывные в обе стороны соответствия, и тогда пространства разной размерности можно будет различить. Эта гипотеза оказалось верной, хотя не такой простой; первые попытки ее доказать, в том числе одна из статей Кантора, содержали ошибки, и только спустя тридцать лет голландский математик Л.Брауэр дал правильное доказательство. Впрочем, отсутствие непрерывного в обе стороны соответствия между отрезком и квадратом доказать несложно; трудности начинаются в больших размерностях. (Заметим также, что существует непрерывное отображение отрезка в квадрат, которое проходит через любую точку квадрата. Оно называется " кривой Пеано".)

Из теоремы 5 легко получить много других утверждений про равномощность геометрических объектов: круг равномощен окружности, прямая равномощна плоскости и т.п.

Можно также заметить, что пространство (точки которого задаются тремя координатами 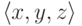) равномощно плоскости (надо закодировать пару 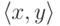одним числом), и, следовательно, прямой. То же самое можно проделать и для пространств большей размерности.

42. Докажите, что множество всех конечных последовательностей действительных чисел равномощно (множеству всех действительных чисел).

43. Докажите, что множество всех бесконечных последовательностей действительных чисел равномощно .

Отметим, что мы пока не умеем доказывать, что множество действительных чисел (или множество бесконечных последовательностей нулей и единиц) несчетно. Это будет сделано в "лекции 4" .

Мощность множества действительных чисел называют мощностью континуума (от латинского слова, означающего "непрерывный"; имеется в виду, что точка на отрезке может непрерывно двигаться от одного конца к другому).