Множества
Число элементов
Число элементов в конечном
множестве  называют также его мощностью
и обозначают
называют также его мощностью
и обозначают 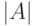 (а также
(а также 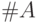 ). (Вскоре мы
будем говорить о мощностях и для бесконечных множеств.)
Следующая формула позволяет найти мощность объединения
нескольких множеств, если известны мощности каждого из них, а
также мощности всех пересечений.
). (Вскоре мы
будем говорить о мощностях и для бесконечных множеств.)
Следующая формула позволяет найти мощность объединения
нескольких множеств, если известны мощности каждого из них, а
также мощности всех пересечений.
Теорема 1. Формула включений и исключений.
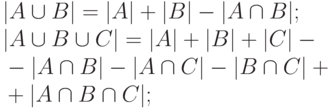
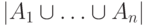 равно
равно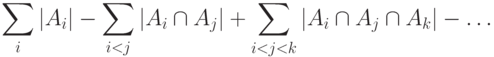
Доказательство.
Это утверждение несложно доказать индукцией по  , но мы
приведем другое доказательство. Фиксируем произвольное
множество
, но мы
приведем другое доказательство. Фиксируем произвольное
множество  , подмножествами которого являются множества
, подмножествами которого являются множества  .
.
Характеристической функцией
множества 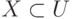 называют функцию
называют функцию 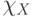 , которая равна
, которая равна  на
элементах
на
элементах  и
и  на остальных элементах
на остальных элементах  . Операции над
подмножествами
множества
. Операции над
подмножествами
множества  соответствуют операциям с их характеристическими
функциями. В частности, пересечению множеств соответствует
произведение характеристических функций:
соответствуют операциям с их характеристическими
функциями. В частности, пересечению множеств соответствует
произведение характеристических функций:  .
Дополнению (до
.
Дополнению (до  )
соответствует функция
)
соответствует функция 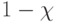 , если
, если 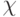 -
характеристическая функция исходного множества.
-
характеристическая функция исходного множества.
Число элементов множества можно записать как сумму значений его характеристической функции:
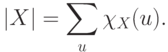
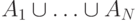 можно записать как
дополнение к пересечению дополнений множеств
можно записать как
дополнение к пересечению дополнений множеств  ;
в терминах характеристических функций имеем
;
в терминах характеристических функций имеем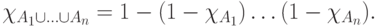
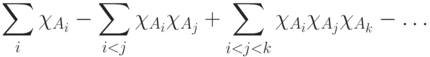
 (обе они есть функции на
(обе они есть функции на  ),
получим формулу включений и исключений.
),
получим формулу включений и исключений.15. Докажите, что 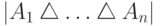 равно
равно
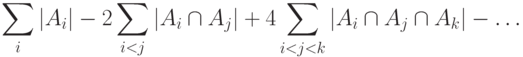
Подсчет количеств элементов в конечных множествах относят к комбинаторике. Некоторые начальные сведения из комбинаторики приведены дальше в качестве задач. Сейчас нас в первую очередь интересует следующий принцип:
если между двумя множествами можно установить взаимно однозначное соответствие, то в них одинаковое число элементов.
(Взаимная однозначность требует, чтобы каждому элементу первого множества соответствовал ровно один элемент второго и наоборот.)
Вот несколько примеров использования этого принципа.
16. На окружности выбраны 1000 белых точек и одна черная. Чего больше - треугольников с вершинами в белых точках или четырехугольников, у которых одна вершина черная, а остальные три белые? (Решение: их поровну, поскольку каждому четырехугольнику соответствует треугольник, образованный тремя его белыми вершинами.)
17. Каких подмножеств больше у  - элементного множества:
мощности
- элементного множества:
мощности 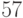 или мощности
или мощности 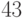 ? (Указание:
? (Указание: 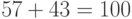 .)
.)
18. Докажите, что последовательностей длины  , составленных из
нулей и единиц, столько же, сколько подмножеств у множества
, составленных из
нулей и единиц, столько же, сколько подмножеств у множества 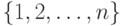 . (Указание: каждому подмножеству
. (Указание: каждому подмножеству 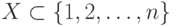 соответствует " характеристическая
последовательность", на
соответствует " характеристическая
последовательность", на  - м месте которой стоит единица,
если и только если
- м месте которой стоит единица,
если и только если  .)
.)
19. Докажите, что последовательностей нулей и единиц длины  ,
в которых число единиц равно
,
в которых число единиц равно  , равно числу
, равно числу  -
элементных
подмножеств
-
элементных
подмножеств  - элементного множества.
- элементного множества.
Это число называется числом сочетаний из n по
k и
обозначается 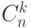 в русских книжках; в
иностранных обычно
используется обозначение
в русских книжках; в
иностранных обычно
используется обозначение 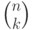 .
.
20. Докажите, что 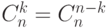 .
.
21. Докажите, что 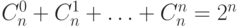 .
.
22. Пусть  - непустое конечное множество. Докажите, что
подмножеств множества
- непустое конечное множество. Докажите, что
подмножеств множества  , имеющих четную мощность, столько же,
сколько имеющих нечетную мощность. (Указание: фиксируем
элемент
, имеющих четную мощность, столько же,
сколько имеющих нечетную мощность. (Указание: фиксируем
элемент  и объединим в пары подмножества, отличающиеся
только
в точке
и объединим в пары подмножества, отличающиеся
только
в точке  .
.
23. Докажите, что 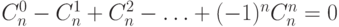 .
(Указание: как это связано с предыдущей задачей?)
.
(Указание: как это связано с предыдущей задачей?)
24. Докажите формулу бинома Ньютона:

25. Докажите, что способов расстановки скобок (указывающих порядок
действий) в неассоциативном произведении из  элементов
столько же, сколько способов разбить выпуклый
элементов
столько же, сколько способов разбить выпуклый 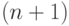 - угольник на треугольники непересекающимися диагоналями.
(Для произведения трех множителей есть два варианта
- угольник на треугольники непересекающимися диагоналями.
(Для произведения трех множителей есть два варианта 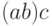 и
и 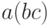 ; с другой стороны, есть два способа разрезать
четырехугольник на два треугольника, проведя диагональ. Для
произведения четырех сомножителей и для пятиугольника имеется по
; с другой стороны, есть два способа разрезать
четырехугольник на два треугольника, проведя диагональ. Для
произведения четырех сомножителей и для пятиугольника имеется по 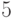 вариантов.)
вариантов.)
