НОУ ИНТУИТ | Введение в математику. Практикум. Лекция 11: Элементы линейной алгебры

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 3447 / 675 | Оценка: 4.05 / 4.28 | Длительность: 03:50:00

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Решение типовых задач линейной алгебры, евклидово пространство, обучение реферированию и Интернет–поиску по этой теме

Ключевые слова: матрица, определитель, собственное число, собственное вектор, характеристическое уравнение, система линейных алгебраических уравнений, метод Гаусса, евклидово пространство

Задачи

Найти матрицы А+В, 3А–2В, А^–1 , В^–1 , если даны матрицы:

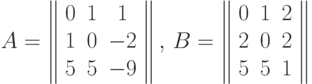
$A=\left\| \begin{array}{ccc} 0&1&1\\1&0&-2\\5&5&-9\end{array}\right \|, \, B=\left\| \begin{array}{ccc} 0&1&2\\2&0&2\\5&5&1\end{array}\right\|$

Указание: использовать соответствующие формулы, например, первый элемент А+В равен a₁₁+b₁₁=0+0=0.
Найти обратную матрицу к матрицам:

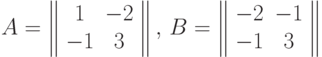
$A=\left\| \begin{array}{cc} 1&-2\\-1&3\end{array}\right \|, \, B=\left\| \begin{array}{cc} -2&-1\\-1&3\end{array}\right \|$

Указание: использовать формулу: $A^{-1}=\cfrac{1}{det(A)}A^*$ .
Найти определитель к матрице

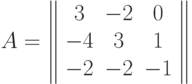
$A=\left\| \begin{array}{ccc} 3&-2&0\\-4&3&1\\-2&-2&-1\end{array}\right \|$

и к ее присоединенной матрице. Найти обратную к А матрицу. Указание: добавить ко второй строке третью и затем разложить по элементам третьего столбца.
Будет ли матрица

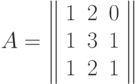
$A=\left\| \begin{array}{ccc} 1&2&0\\1&3&1\\1&2&1\end{array}\right \|$

симметричной, диагональной, нулевой, единичной, имеющей нулевой определитель? Указание: все ответы – отрицательные (обоснуйте это!).
Найти определитель, транспонированную, союзную и обратную матрицу для матрицы

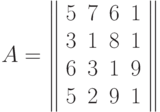
$A=\left\| \begin{array}{cccc} 5&7&6&1\\3&1&8&1\\6&3&1&9\\5&2&9&1\end{array}\right \|$

Указание: для вычисления определителя вычесть первую строку из второй и четвертой, затем умножить первую строку на 9 и вычесть из третей строки, после чего разложить по элементам первой строки.
Показать, что

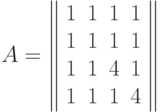
$A=\left\| \begin{array}{cccc}1&1&1&1\\1&1&1&1\\1&1&4&1\\1&1&1&4\end{array}\right \|$

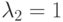имеет собственные числа $\lambda _{1}=0$ , $\lambda _{2}=1$ , $\lambda _{2}=3$ , $\lambda _{4}=6$ и собственные вектора:

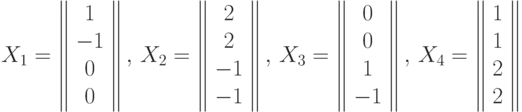
$X_1=\left\| \begin{array}{c}1\\-1\\0\\0\end{array}\right \|, \, X_2=\left\| \begin{array}{c}2\\2\\-1\\-1\end{array}\right \|, \, X_3=\left\| \begin{array}{c}0\\0\\1\\-1\end{array}\right \|, \, X_4=\left\| \begin{array}{c}1\\1\\2\\2\end{array}\right \|$

Указание: выписать матричное характеристическое уравнение, записать соответствующей ему линейную систему алгебраических уравнений и решить ее.
Решить методом Крамера и Гаусса систему:

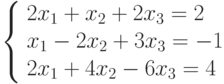
$\left\{\begin{array}{l} 2x_1+x_2+2x_3=2\\ x_1-2x_2+3x_3=-1\\2x_1+4x_2-6x_3=4\end{array} \right$

Оценить количество выполненных арифметических операций в каждом методе и сравнить их. Какой метод более эффективный? Указание: подсчитывать все операции – и те, которые необходимы для исключения неизвестных в методе Гаусса, и те, которые необходимы для нахождения определителя в методе Крамера.
Найти, если есть, решение системы линейных алгебраических уравнений:

$\left\{\begin{array}{l} 2x_1+x_2+2x_3+x_4=2\\ x_1-2x_2+3x_3-x_4=-1\\2x_1+4x_2-6x_3+3x_4=4\end{array} \right$

Указание: найти ранг системы, далее, перенести, например, х₄ во всех уравнениях в правую часть и решить затем, считая х₄ известным, задаваемым произвольно числом.
Проверить для произвольной матрицы А выполнение аксиом нормы, если норму определять одним из способов:
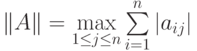- $\|A\| = \max\limits_{1\le j \le n}\sum\limits_{i=1}^n{|a_{ij}|}$ ;
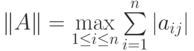- $\|A\| = \max\limits_{1\le i \le n}\sum\limits_{i=1}^n{|a_{ij}|}$ ;
- $\|A\| = |\det{(A)}|$
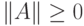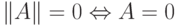Указание: а) $\|A\|\ge0$ ; б) $\|A\|=0 \Leftrightarrow A=0$ ; в) $\|A+B\|\le\|A\|+\|B\|$ .
Древнекитайская задача: в одной клетке сидят фазаны и кролики, а всего в ней 35 голов и 94 ноги; сколько фазанов и кроликов в клетке? Указание: если x – число фазанов, y – число кроликов, то по условию задачи y=35, 2x+4y=94.