Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 3507 / 690 | Оценка: 4.05 / 4.28 | Длительность: 03:50:00
Тема: Математика
Специальности: Математик
Практическая работа 10:
Комбинаторика и числовые системы
< Самостоятельная работа 3 || Практическая работа 10 || Самостоятельная работа 4 >
Аннотация: Решение типовых задач комбинаторики (вычисление факториала, перестановки, подстановки, размещения, сочетания) и теории чисел, обучение реферированию и Интернет–поиску по этой теме
Ключевые слова: математическая индукция, перестановка, подстановка, сочетание, бином Ньютона, Числа Ферма, число Мерсенна, Числа Паскаля, методы суммирования
Задачи
- Докажите методом математической индукции формулу суммы членов арифметической прогрессии. Указание: формула –
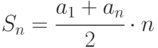 .
. -
Записать для общего случая и с помощью знаков суммы и произведения неравенства:

Указание: найти индуктивно формулу
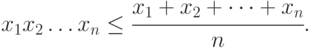
- Вычислите наиболее эффективно дробь (7!)/(5!). Указание: представить числитель через знаменатель.
-
Решить рекуррентное уравнение:
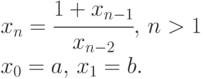
Указание: найти х3, затем х4 и получить соответствующую формулу для xn.
-
Найдите формулу общего члена последовательности, удовлетворяющего рекуррентному соотношению:
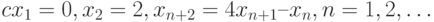
Указание: найти х2, затем х3 и т.д.
- Имеется аудиторская фирма из 10 сотрудников. Сколько можно сформировать различных аудиторских групп фирмы по 5 человек? Сколько можно сформировать аудиторских групп численностью от 1 до 10 человек? Какие группы еще можно формировать и как находить их количество? Указание: использовать формулы для перестановок, подстановок и сочетаний.
- Вычислить по биному Ньютона 1,15. Как можно использовать формулу бинома Ньютона для приближенных вычислений? Указание: представить 1,1 как 1+0,1 и затем разложить по формуле бинома Ньютона.
-
Вычислить наиболее эффективно суммы:
-
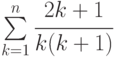 ;
; -
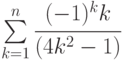 ;
; -
 .
.
Указание: а) представить 2k+1=k+k+1 и затем осуществить почленное деление; б) сгруппировать попарно все последовательные слагаемые и рассмотреть отдельно эти разности; в) сгруппировать.
-
- Вычислите числа Ферма и Мерсенна при n=4. Указание: выписать таблицу этих чисел и проанализировать.
- Постройте треугольник Паскаля при n=12. Указание: выписать числа, отражающие эту "треугольную таблицу".
Темы научных исследований и рефератов (Интернет-листов)
- "Простая" и математическая индукция.
- Рекурсия, ее приложения в социально-гуманитарных областях. Примеры.
- Комбинаторика, ее различные приложения в социально-гуманитарных областях. Примеры.
- Теоремы суммирования и перемножения.
- Роль формул сокращения записей в математике и приложениях. Примеры.
- Мировоззренческая роль математики древних и средних веков.
- Красота математических формул. Примеры.
- Бином Ньютона, его приложения. Примеры.
- Цифровые системы. Примеры.
- Арифметика (алгебра чисел).
< Самостоятельная работа 3 || Практическая работа 10 || Самостоятельная работа 4 >
