НОУ ИНТУИТ | Введение в математику. Практикум. Лекция 7: Предельный переход и непрерывность

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 3447 / 675 | Оценка: 4.05 / 4.28 | Длительность: 03:50:00

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 47 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Решение типовых задач на предельный переход в числовых последовательностях, предел и непрерывность функции, замечательные пределы, бесконечно малые и бесконечно большие величины, основные типы неопределенностей, обучение реферированию и Интернет–поиску по этой теме

Ключевые слова: предел, последовательность, бесконечно малая величина, бесконечно большая величина, замечательный предел, бесконечно большие и малые величины, неопределенность

Задачи

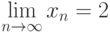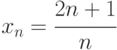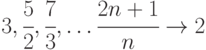Покажите, по определению предела последовательности, что $\lim\limits_{n\to\infty} x_n =2$ , где $x_n = \cfrac{2n+1}{n}$ , т.е. $3,\cfrac52,\cfrac73,\dots\cfrac{2n+1}{n}\to2$ Указание: оценить сверху модуль .
Найти пределы:
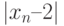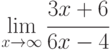- $\lim\limits_{x\to\infty} \cfrac{3x+6}{6x-4}$ ,
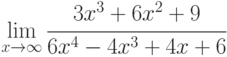- $\lim\limits_{x\to\infty} \cfrac{3x^3+6x^2+9}{6x^4-4x^3+4x+6}$ ,
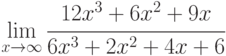- $\lim\limits_{x\to\infty} \cfrac{12x^3+6x^2+9x}{6x^3+2x^2+4x+6}$ .
Указание:
- разделить числитель и знаменатель на х ;
- разделить числитель и знаменатель на х⁴ ;
- разделить числитель и знаменатель на х³.
Какие функции являются бесконечно малыми, а какие – бесконечно большими при x->x₀ :
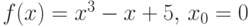- $f(x)=x^3-x+5,\,x_0=0$ ;
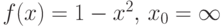- $f(x)=1-x^2,\,x_0=\infty$ ;
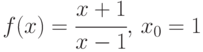- $f(x)=\cfrac{x+1}{x-1},\,x_0=1$ ?
Ответ обосновать. Указание: найти предел f(x) при x->x₀ .
Вычислить пределы:
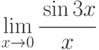- $\lim\limits_{x\to0}\cfrac{\sin3x}{x}$ ;
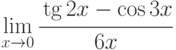- $\lim\limits_{x\to0}\cfrac{\tg{2x}-\cos{3x}}{6x}$ ;
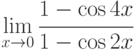- $\lim\limits_{x\to0}\cfrac{1-\cos{4x}}{1-\cos{2x}}$ .
Указание: а) умножить и разделить дробь на 3, а затем использовать первый замечательный предел ; б) представить тангенс через синус и косинус; в) использовать формулу 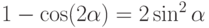$1 - \cos(2\alpha ) = 2 \sin^{2}\alpha$ и затем формулу синуса двойного угла.
Вычислить пределы:
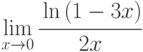- $\lim\limits_{x\to0}\cfrac{\ln{(1-3x)}}{2x}$ ;
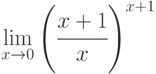- $\lim\limits_{x\to0}\left(\cfrac{x+1}{x}\right)^{x+1}$ ;
- $\lim\limits_{x\to\infty}\left(\cfrac{x+8}{x-2}\right)^{x}.$
Указание: использовать второй замечательный предел.
Показать, что функция

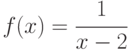
$f(x)=\cfrac{1}{x-2}$
имеет разрыв при x=2. Есть ли еще у этой функции разрыв? Указание: оценить отдельно пределы для x<2 и для x>2 при x $\to$ 2.
В какой точке имеет разрыв функция

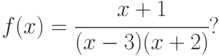
$f(x)=\cfrac{x+1}{(x-3)(x+2)}?$

Указание: исследовать значения х, для которых f(x) стремится к бесконечности.
Исследовать на непрерывность в области R функцию вида:
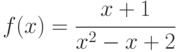- $f(x)=\cfrac{x+1}{x^2-x+2}$ ;
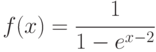- $f(x)=\cfrac{1}{1-e^{x-2}}$ ;
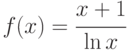- $f(x)=\cfrac{x+1}{\ln x}$ .
Указание: исследовать значения – 1. x=–1 ; x=2 ; 2. x=2 ; 3. х=0.
Выяснить, имеет ли разрыв функция вида (и, если имеет, то в какой точке):
- $y=\tg x$ ;
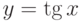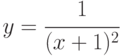- $y=\cfrac{1}{(x+1)^2}$ ;
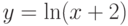- $y=\ln(x+2)$ .
Указание: исследовать значения – 1. x=0 ; 2. x= –1 ; 3. х= – 2.
Оценить по теореме Вейерштрасса максимальное и минимальное значения функции

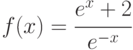
$f(x)=\cfrac{e^x+2}{e^{-x}}$

Указание: проверить непрерывность f(x) (применимость теоремы).