Опубликован: 22.01.2008 | Доступ: свободный | Студентов: 3447 / 675 | Оценка: 4.05 / 4.28 | Длительность: 03:50:00
Тема: Математика
Специальности: Математик
Теги:
Самостоятельная работа 2:
Множества, отношения и их использование
< Практическая работа 6 || Самостоятельная работа 2 || Практическая работа 7 >
Аннотация: Развитие исследовательских и творческих навыков по сопоставлению различных совокупностей друг другу, поиску и описанию различных отношений, функций
Ключевые слова: множество, пересечение, объединение, функция, отношение, классификация, эквивалентность, отображение, композиция, соответствие, класс
- Доказать свойство множеств:
. Указание: взять произвольный элемент из правой части равенства и показать, что он принадлежит левой части и наоборот. - Записать и доказать свойство, двойственное свойству из предыдущей задачи. Указание: двойственность означает, что пересечение можно "заменить" объединением и наоборот; взять произвольный элемент из правой части равенства и показать, что он принадлежит левой части и наоборот.
- Привести примеры, показывающие, что не всякая формула задает функцию. Указание: чтобы формула задавала функцию, необходимо "согласие" областей определения и изменения функции и их "непустота".
- Привести примеры, показывающие, что не всякую функцию можно задать в виде формулы. Указание: чтобы функцию можно было бы задать формулой, необходима ее формализация, что не обеспечивается всеми способами.
- Пусть даны функции z=1/у, у=cos(х). Найти область определения и область изменения функции z. Указание: знаменатель дроби не может никогда обращаться в нуль.
- Сформулируйте отношение, которое позволяет классифицировать студентов факультета по успеваемости, с целью назначения стипендий. Указание: например, это может быть отношение, содержательно задаваемое на всем множестве студентов факультета словами "студент успевает по всем предметам"; формализуйте такое отношение и проверьте, что это отношение эквивалентности.
- Даны процессы перевода с русского языка на английский язык (грамматические отображения текстов на русском языке в тексты на английском языке) или отображение текстов
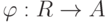, с английского – на немецкий ( отображение текстов 
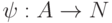), c немецкого – на французский ( f : N->F ). Выясните смысл отображения: 
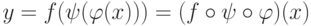. Указание: композиция 
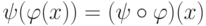представляет перевод текста х на русском языке на английский язык, а затем перевод полученного текста 
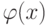на английском языке в текст 
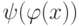на немецком языке. - Выяснить какие отношения ( соответствия ) определяют диаграммы 1-8, приведенные ниже и однозначность этих соответствий. Указание: вспомнить определение соответствия, однозначного, взаимнооднозначного и т.д.
-
Запишите классы, на которые разбивается множество всех целых чисел Z равенством x=y+ka, x, y, k,
для:- k=1 ;
- k=2 ;
- k=3.
Указание: это равенство означает, что при делении на a (или k ) число х дает в остатке число y.
-
Пусть
Х={Иванов, Петров, Сидоров, физика, математика, 12.01.06, 18.01.06, 19.01.06, 21.01.06, 4, 5, 3, 3},а отношения r1 и r2 заданы, соответственно, как
"студент–успеваемость", "студент–дата сдачи экзамена".
Запишите таблично отношения r1or2, r2or1. Указание: сделать таблицы, иллюстрирующие указанные отношения, например, таблицу со строками – Иванов, Петров, Сидоров и столбцами физика, математика, в ячейках которого указываются числа или даты.
< Практическая работа 6 || Самостоятельная работа 2 || Практическая работа 7 >
